選擇公理

選擇公理（英語：Axiom of Choice，縮寫AC）是數學中的一條集合論公理，用來證明一些難以明確構造的物件的存在性。選擇公理最早於1904年，由恩斯特·策梅洛為了證明良序定理而作為一條公理加入^[1]。

(S_i) 是一個以實數集R為指標集的集族；也就是說，對每一個實數i，均存在一個集合 S_i，如圖所示。每一個集合包含至少一個（可能是無限個）元素。選擇公理可以斷言，我們可以從每一個集合中選擇一個元素，組成一個在R上的索引族(x_i)，這裏x_i∈S_i，i∈R。一般情況下，指標集可以是任意集合I，而不僅僅是R。

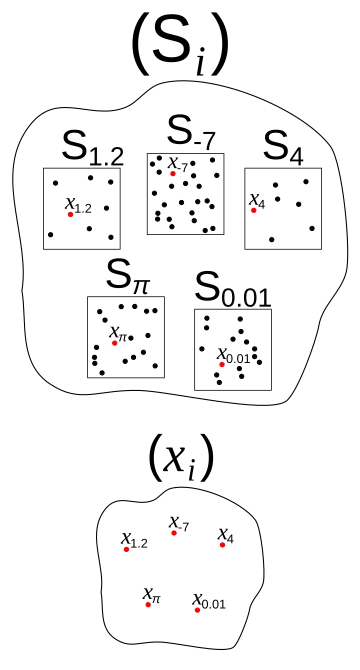
非正式地說，給定一些盒子（可以是無限個），每個盒子中都含有至少一個小球，這時選擇公理相當於是在說——可以從每個盒子裏拿出一顆球。在很多情況下這樣的選擇並不需要藉助選擇公理；尤其是在「盒子個數有限」或「盒子內的球具有額外的特徵」這兩種情況下，經常可以直接指明選擇的方式。關於「存在具體的選擇方式」可以透過以下例子理解：假設有許多（甚至是無限）雙鞋子，則可以選取每雙鞋左邊的鞋子構成一個具體的選擇，由於在鞋子之中「存在具體的選擇規則」(左邊的鞋子不同於右邊的鞋子)，所以即使沒有選擇公理也依然可以做出具體的選擇。但是，如果把鞋子改成襪子，且每雙襪子都沒有可區分的特徵，在這種情況下，「選擇的存在性」只能通過選擇公理得到。

儘管曾經具有爭議，選擇公理現在已經被大部份數學家毫無保留地使用着^[2]，例如帶有選擇公理的策梅洛-弗蘭克爾集合論（ZFC）。數學家們使用選擇公理的原因是，有許多被普遍接受的數學定理，比如是吉洪諾夫定理，都需要選擇公理來證明。現代研究集合論的數學家也研究與選擇公理相矛盾的公理，例如決定公理。

在一些構造性數學的理論中會避免選擇公理的使用，不過也有的將選擇公理包括在內。

陳述

首先定義幾個概念：

集族：指由非空集合組成的集合。

選擇函數：它是一個集族上的函數。它規定：對於所有在集族${\displaystyle X}$中的集合${\displaystyle s}$，${\displaystyle f(s)}$是${\displaystyle s}$的一個元素。

那麼，選擇公理表示：

對於所有的集族，均存在選擇函數。

上述可表示為：

${\displaystyle \forall X\left[\emptyset \notin X\implies \exists f\colon X\rightarrow \bigcup X\quad \forall A\in X\,(f(A)\in A)\right]\,.}$

或者：

設${\displaystyle X}$是一個集族，則存在着在${\displaystyle X}$上定義的一個選擇函數${\displaystyle f}$。

該定理也可表達為：

集族上的任意笛卡爾積總是非空的。

變體

第二個版本的選擇公理聲稱：

給定由相互不交的非空集合組成的任何集合，存在着至少一個集合，它與每個非空集合恰好有一個公共元素。

第三個版本聲稱：

對於任何集合${\displaystyle A}$，${\displaystyle A}$的冪集（減去空集）有一個選擇函數。

使用這個版本的作者通常談及「在${\displaystyle A}$上的選擇函數」，但要注意這裏選擇函數的概念是稍微不同的。它的定義域是${\displaystyle A}$的冪集（減去空集），因此對任何集合${\displaystyle A}$有意義；至於本文中其他地方用的定義，在「集合的搜集」上的選擇函數的定義域是這個搜集，所以只對集合的集合有意義。透過這個變體的定義，選擇公理也可以簡潔的陳述為

所有集合有一個選擇函數。^[3]

它等價於

對於任何集合${\displaystyle A}$有一個函數使得對於${\displaystyle A}$的任何非空子集${\displaystyle B}$，${\displaystyle f(B)\in B}$。

而選擇公理的否定表達為：

有一個集合${\displaystyle A}$使得對於所有函數${\displaystyle f}$（在${\displaystyle A}$的非空子集的集合上），有一個${\displaystyle B}$使得${\displaystyle f(B)\notin B}$。

術語（AC，ZF，ZFC）

以下列出了這篇條目中各種與「選擇公理」相關的縮寫：

• AC：選擇公理。
• ZF：策梅洛-弗蘭克爾集合論，不包括選擇公理。
• ZFC：策梅洛-弗蘭克爾集合論，包括選擇公理。

使用

直到19世紀晚期，選擇公理的使用一直都沒有得到明確聲明。例如，建立了只包含非空集合的集合${\displaystyle X}$之後，當時的數學家可能會直接說「設對於${\displaystyle X}$中所有${\displaystyle s}$有${\displaystyle F(s)}$是${\displaystyle s}$的成員之一」。一般來說，要是不用選擇公理，是不可能證明${\displaystyle F}$的存在性的。這一點直到策梅洛之前似乎沒有引起人們的注意。

不是所有的情況都需要選擇公理。選擇公理對於那些沒有可定義的選擇才有必要。值得指出的是，對於有限集合${\displaystyle X}$，選擇公理的有限版本可以通過其他集合論公理推導得出。在這種情況下，它等價於說我們有多個（有限數目的）盒子，每個包含至少一個物體，則我們可以從每個盒子恰好選擇一個物體。顯然我們可以這麼做：從第一個盒子開始，選擇其中的一個物體；到下一個盒子，選擇一個物體；如此類推。因為盒子數量有限，所以我們的選擇過程最後一定會結束。這裏給出的選擇函數是明確的：第一個盒子對應於第一個選擇的物體，第二個盒子對應於第二個選擇物體；如此類推——此法之所以可行，是因為序對公理的原因。可以通過數學歸納法做出對所有有限集合的形式證明。

例子

對於特定的無限集合${\displaystyle X}$，也可以避免使用選擇公理。例如，假設${\displaystyle X}$的元素是自然數的集合。每個自然數的非空集合都有一個最小的自然數，所以只要簡單的把每個集合映射到這個集合內最小的數字，就得到了選擇函數。這使得我們可以從每個集合明確地選擇元素，以及寫出一個明確的表達式，說明我們的選擇函數如何取值。在能夠指定一個明確選擇方式的時候，選擇公理都是沒有必要的。

當缺乏從每個集合得到元素的直觀選擇方式時，困難就出現了。如果不知道選擇的方式，那要怎麼確認選擇函數的存在？例如，假設X是實數的所有非空子集的集合。第一個可能產生的思路是套用有限的情況去處理${\displaystyle X}$。如果嘗試從每個集合選擇一個元素，那麼，因為實數集合是無限不可數，所以選擇的過程永遠不會結束。也因為如此，永遠不能構造出對${\displaystyle X}$的成員的選擇函數。所以這種方法不能奏效。第二個可能產生的思路是嘗試給每個集合指定最小元素，但是很多實數的子集沒有最小元素。例如，開區間${\displaystyle (0,1)}$沒有最小元素：如果${\displaystyle x}$在${\displaystyle (0,1)}$中，則${\displaystyle {\frac {x}{2}}}$也在其中，而${\displaystyle {\frac {x}{2}}}$總是嚴格的小於${\displaystyle x}$。所以這種方法也不行。

我們之所以能夠從自然數的非空子集選擇最小元素，是因為自然數上有一個良序：所有自然數的非空子集都有一個唯一的最小元素。

因此，第三個思路，「即使實數的正常排序方式不是良序，是不是也能找到一個排序使得實數是良序的？」。如果真的有這種排序方式，那就能夠選擇實數非空子集的最小元素，從而得到了選擇函數——然而問題就變成如何構造這樣的排序。而事實上，「存在一個排序使得所有集合是良序的」等價於選擇公理。

有必要用到選擇公理的證明總是非構造性的，即使證明給出了一個物件，精確地說出那個物件卻是不可能的。如果不能寫出選擇函數的定義，那這個選擇到底是什麼？這是一些數學家不喜歡選擇公理的理由之一。例如，構造主義者論斷說所有涉及存在性的證明都應當是完全明確的；構造任何存在的物件應當是可能的。他們拒絕選擇公理^{[來源請求]}，因為它斷言了「不能具體描述的物件」存在。

構造性數學

像上面討論的那樣，在ZFC中，選擇公理能為一個不能明確構造出的物件給出「非構造性證明」來證明其存在性。然而，ZFC依然是在經典邏輯下被形式化的。在構造性數學領域，選擇公理仍被深入研究，而當中應用的是非古典邏輯。在構造性數學的不同版本中，選擇公理的狀況也有所差別。

在直覺類型論和高階的Heyting算術（英語：Heyting arithmetic）中，選擇公理的適當陳述（按照推導方式）可以是作為一個公理，又或者作為一個可證明的定理^[4]。埃里特‧畢夏普（英語：Errett Bishop）認為選擇公理可被視作是構造性的^[5]：

“

在構造性數學中選擇函數是存在的，因為存在的涵義蘊涵了選擇。

”

但在構造性集合論（英語：Constructive set theory）中，迪亞科內斯庫定理表明選擇公理蘊涵了排中律（在直覺類型論中，選擇公理不蘊涵排中律）。因此選擇公理在構造性集合論中並非普遍被接受。在類型論中的選擇公理與在構造性集合論中的選擇公理的區別是，前者不具有外延性而後者具有^[6]。

一些構造性集合論的結果用到了可數選擇公理或依賴選擇公理，這兩個公理在構造性集合論內並不蘊涵排中律。儘管可數選擇公理在構造性數學中的應用特別廣泛，它的使用也受到質疑^[7]。

強形式公理

可構造性公理與連續統假設都蘊涵了選擇公理，更準確地說，兩者都嚴格強於選擇公理^[8]。在類理論中，如馮諾伊曼-博內斯-哥德爾集合論和Morse–Kelley集合論，存在一個叫全局選擇公理的公理，它比選擇公理要強，因其同時也適用於真類。全局選擇公理可由大小限制公理推出。

結論

哥德爾證明了選擇公理與ZF的相對協調性。保羅·寇恩用力迫法證明了選擇公理獨立於ZF。

參考文獻

引用

1. Zermelo 1904 harvnb error: no target: CITEREFZermelo1904 (help).
2. Jech, 1977, p. 348ff; Martin-Löf 2008, p. 210. According to Mendelson 1964，第201頁 harvnb error: no target: CITEREFMendelson1964 (help): The status of the Axiom of Choice has become less controversial in recent years. To most mathematicians it seems quite plausible and it has so many important applications in practically all branches of mathematics that not to accept it would seem to be a wilful hobbling of the practicing mathematician.
3. Patrick Suppes, "Axiomatic Set Theory", Dover, 1972 (1960), ISBN 978-0-486-61630-8, pp 240
4. Per Martin-Löf, Intuitionistic type theory （頁面存檔備份，存於互聯網檔案館）, 1980. Anne Sjerp Troelstra, Metamathematical investigation of intuitionistic arithmetic and analysis, Springer, 1973.
5. Errett Bishop and Douglas S. Bridges, Constructive analysis, Springer-Verlag, 1985.
6. Per Martin-Löf, "100 Years of Zermelo’s Axiom of Choice: What was the Problem with It?", The Computer Journal (2006) 49 (3): 345-350. doi: 10.1093/comjnl/bxh162
7. Fred Richman, 「Constructive mathematics without choice」, in: Reuniting the Antipodes—Constructive and Nonstandard Views of the Continuum (P. Schuster et al., eds), Synthèse Library 306, 199–205, Kluwer Academic Publishers, Amsterdam, 2001.
8. Devlin, Keith. Constructibility. Springer-Verlag. 1984. ISBN 3-540-13258-9.

來源

• Ernst Zermelo, "Untersuchungen über die Grundlagen der Mengenlehre I," Mathematische Annalen 65: (1908) pp. 261-81. PDF download via digizeitschriften.de

Translated in: Jean van Heijenoort, 2002. From Frege to Godel: A Source Book in Mathematical Logic, 1879-1931. New edition. Harvard Univ. Press. ISBN 978-0-674-32449-7.

• 1904. "Proof that every set can be well-ordered," 139-41.
• 1908. "Investigations in the foundations of set theory I," 199-215.

• Gregory H Moore, "Zermelo's axiom of choice, Its origins, development and influence", Springer; 1982. ISBN 978-0-387-90670-6.
• Paul Howard and Jean Rubin, "Consequences of the Axiom of Choice". Mathematical Surveys and Monographs 59; American Mathematical Society; 1998.

外部連結

• Paul Howard at EMU （頁面存檔備份，存於互聯網檔案館）有很多人仍然在為選擇公理和它的推論而樂此不疲地工作。如果你有興趣了解更多內容，請參考這個網站。

參見

• 數學主題

• 集合論
• 佐恩引理
• 良序定理
• 吉洪諾夫定理
• 策梅洛-弗蘭克爾集合論
• 馮諾伊曼-博內斯-哥德爾集合論
• 全局選擇公理
• 可數選擇公理
• 連續統假設
• 排中律
• 直覺類型論