商空間

本文介紹拓撲學中的商空間，線性代數中的商空間參見商空間。

在拓撲學及其相關數學領域，一個商空間（quotient space，也稱為等化空間identification space）直觀上說是將一個給定空間的一些點等同或「黏合在一起」；由一個等價關係確定哪些點是等同的。這是從給定空間構造新空間的常見方法。

定義

假設X是一個拓撲空間，~是X上一個等價關係。我們能夠在商集合X/~（這個集合有所有~的等價類組成）上定義一個拓撲使得：X/~中一個等價集合是開集若且唯若他們的併集在X中是開集。所得的拓撲稱為在商集合X/~上的商拓撲（quotient topology）。

商拓撲可以由如下方式等價地定義：設q : X → X/~是將X的任何元素映為它的等價類的投影映射（${\displaystyle x\mapsto [x]}$）。則X/~上的商拓撲定義為使q 連續的最細拓撲（finest topology）。

給定一個從拓撲空間X到集合Y的滿射f : X → Y，我們可以在Y上定義商拓撲為使f連續的最細拓撲。這等價於說集合V ⊆ Y在Y中開若且唯若它的原像f⁻¹(V)在X中開。映射f在X上誘導了一個等價關係，即x₁~x₂若且唯若f(x₁) = f（x₂）。這個商空間X/~ 同胚於Y（帶着它的商拓撲），同構映射為將x的等價類映為f(x)。

一般地，如果Y具有由一個滿連續映射f : X → Y確定的商拓撲，則f稱為一個商映射（quotient map）。

例子

• 黏合：通常，拓撲學家討論將一些點黏合在一起。如果X是一個拓撲空間，點${\displaystyle x,y\in X}$「黏合」在一起，這意味着我們考慮由等價關係a~b若且唯若a = b或a = x, b = y（或a = y, b = x）得到的商空間。即這兩個點被看作一個。
• 考慮一個單位正方形I² = [0,1]×[0,1]以及由所有邊界點等價生成的等價關係~，從而所有邊界點等同到一個等價類。則I²/~同構於單位球面S²。
• 黏着空間（Adjunction space）：更一般地，假設X是一個空間，A是X的一個子空間。我們可以將A中所有點等同到一個等價類，而A以外的點不變。所得的空間記作X/A。2維球面同構於將單位圓盤的邊界等同為一個點D²/∂D²。
• 考慮集合X = ${\displaystyle \mathbb {R} }$，取通常拓撲的實數集，記x ~ y 若且唯若x−y是一個整數。則商空間X/~同構於單位圓周S¹，同構映射為將x的等價類映為 exp（2πix）。
• 上一個例子的一類大量的推廣如下：假設一個拓撲群G連續作用在空間X上。我們可以構造X上一個等價關係，如果兩點等價若且唯若它們在同一個軌道中。這個關係下的商空間稱為軌道空間，記作X/G。上一個例子中G = ${\displaystyle \mathbb {Z} }$通過平移作用在${\displaystyle \mathbb {R} }$上。軌道空間${\displaystyle \mathbb {R} /\mathbb {Z} }$同構於S¹。

注：記號${\displaystyle \mathbb {R} /\mathbb {Z} }$有歧義：如果${\displaystyle \mathbb {Z} }$理解成一個群作用在${\displaystyle \mathbb {R} }$上則商空間是圓周；如果${\displaystyle \mathbb {Z} }$看作${\displaystyle \mathbb {R} }$的一個子空間，則商空間是無窮的一束圓（英語：bouquet of circles）在同一個點連接起來。

性質

商映射 q : X → Y是由如下性質刻畫的滿射：如果Z是任何拓撲空間，f : Y → Z是任何函數，則f連續若且唯若f O q連續。

商空間的特徵性質

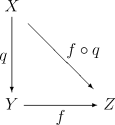
商空間X/~與商映q : X → X/~一起由如下泛性質刻畫。如果g : X → Z是一個連續映射使得：對所有a與b屬於X，a~b蘊含g(a)=g(b)，則存在惟一連續映射f : X/~ → Z使得g = f O q。我們稱 g「下降到商」。

因此定義在X/~商的連續映射恰是由定義在X上與等價關係一致的連續映射（它們將同一個等價類中的元素映到相同的像）誘導的。在研究商空間時，時常使用這個判據。

給定一個連續滿射f : X → Y，關於f是否為商映射的判據是有用的。兩個充分條件是f為開映射或閉映射。注意這兩個條件只是充分條件而不是必要的。容易構造出不開或不閉的商映射例子。

與其它拓撲概念的相容性

• 分離
  • 一般地，商空間關於分離公理的表現都很壞。X的分離性質不必被X/~繼承，而X/~可能具有X所沒有的分離性質。
  • X/~是一個T1空間若且唯若~的任何等價類在X中閉。
  • 如果商映射開則X/~是一個豪斯多夫空間若且唯若~是乘積空間X×X的一個子集。
• 連通性
  • 如果一個空間是連通的或道路連通，則所有的商空間也是。
  • 一個單連通或可縮空間的商空間不必具有同樣的性質。
• 緊性
  • 如果一個空間緊，則所有商空間也是。
  • 一個局部緊空間的商空間不必是局部緊的。
• 維數
  • 一個商空間的拓撲維數可能比原空間大（顯然也可能比較小），皮亞諾曲線（space-filling curve）提供了這樣的例子。

又見

拓撲學

• 子空間
• 乘積空間
• 不交並
• 最終拓撲（英語：Final topology）

代數

• 商群
• 商空間
• 商範疇

參考

• Stephen Willard, General Topology, (1970) Addison-Wesley Publishing Company, Reading Massachusetts.
• Quotient space. PlanetMath.