Loading AI tools
图论理论 来自维基百科，自由的百科全书
網絡理論（Network theory）是一種對圖的研究，也是對稱關係或不對稱關係在離散對象中的一種表現。 在計算機科學和網絡科學中 ，網絡理論是圖論的一部分：網絡可以定義為節點和/或邊具有屬性（例如名稱）的圖。
 |
網絡理論目前在許多學科中有應用，學科包括統計物理學、粒子物理學、計算機科學、電氣工程學[1][2]、生物學、[3]經濟學、金融學、運籌學、氣候學、生態學和社會學；應用包括物流網、萬維網、互聯網、基因調控網絡、代謝網絡、社會網絡、知識論網絡等。
在名稱組合優化的模塊中，人們正在研究涉及到尋找某類事務最優路徑的網絡問題。 其實例包括 網絡流問題、最短路徑問題、運輸問題、轉運問題、選址問題、匹配問題、分配問題、包裝問題、路由問題、關鍵路徑分析與計劃評審技術（項目評估與審查技術）。 為了將網絡優化的一個NP困難任務分解成子任務。網絡被分解為相對獨立的子網絡[5]
電力系統的分析可以利用網絡理論從兩個主要角度進行:
1.一個抽象的網絡(例如一個圖包括節點和邊)，不考慮其電力模塊(例如傳送線路受阻抗影響)。 這些研究大多數集中在抽象電網結構其節點的度與介數的分佈上，而該分佈引入了關於網格脆弱性評估的實質性見解。通過這些類型的研究，網格結構的類別可以從網絡結構的複雜度（例如，單尺度、無尺度）確定。 這種分類可能有助於電力系統工程師在規劃階段或在升級基礎設施（例如，增加一條新的輸電線路）時保持輸電系統的適當冗餘水平。[1]
2.摻雜了對複雜網絡理論與電力系統特性的抽象理解的加權圖。[2]
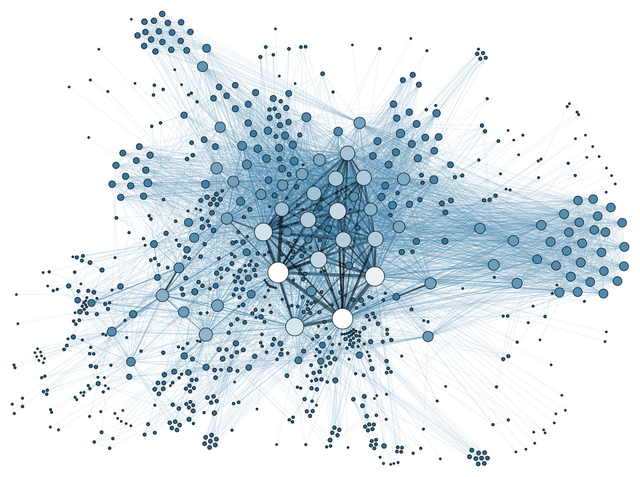
社會網絡分析研究社會實體之間的關係結構。[7]這些實體通常是個人，但也可能是團體、組織、國家、網站或學術出版物。
自20世紀70年代以來，對網絡的實證研究在社會科學中處於核心地位，許多用於研究網絡的數學和統計學工具最早是在社會學中發展起來的。[8]在許多其他應用中，社交網絡分析被用來解釋創新、新聞和謠言的傳播。類似地，它也被用來檢測疾病和健康相關行為的傳播。在市場研究中，它還被用來研究信任在交換關係中與社會機制在物品定價中的作用。除此以外，它還被用來研究政治運動和社會組織的招新問題，以及被用來將科學分歧和學術聲望觀念化。最近，網絡分析（以及它的近親流量分析）在軍事情報中獲得了重要的應用，用於揭露有等級與無領導群體的叛亂網絡。
隨着近年來公開的高通量生物數據的激增，分子網絡分析引起了人們極大的興趣。[9]這種背景下的分析類型與社會網絡分析密切相關，但更關注網絡中的局部模式。例如，網絡基元是在網絡中被過度表示的小型子圖。類似地，活動基元是在給定網絡結構中節點和邊被過度表示的模塊屬性。利用網絡來分析生物系統的模式，例如食物網，可以讓我們看到物種之間相互作用的特徵和強度。對疾病生物網絡的分析，促進了網絡醫學的發展。[10]網絡理論在生物學中應用的最新例子包括對細胞周期的理解。[11]腦、心、眼等生理系統之間的相互作用可以看作是一個生理網絡。[12]
語料庫的自動解析在很大程度上實現了角色及其關係網絡的提取。然後，使用網絡理論中的工具分析可產生包含數千個節點的敘事網絡，從而確定關鍵角色、關鍵社區或團體，並確定其常規屬性如總體網絡的魯棒性或結構穩定性，以及某些節點的中心性等。[14]這針對定量敘事分析引入自動化的方法，即主謂賓結構被識別為不同角色由一個動作連接或由一對主賓結構組成。[15][13]
連結分析是網絡分析的一個子集，其研究對象之間的關聯性。例如，作為警方調查的一部分，其可以檢查犯罪嫌疑人和受害者的地址、他們撥打的電話號碼、他們在特定時間內參與的金融交易，以及這些對象之間的家庭關係。連結分析在此提供了許多不同類型的對象之間的關鍵關係和關聯，而其在獨立的信息片段中並不明顯。計算機輔助或全自動的連結分析越來越多地被使用在各個方面，其中包括銀行和保險機構進行欺詐檢測，電信運營商進行電信網絡分析，醫療部門進行流行病學和藥理學分析以及執法調查，搜尋引擎進行相關性評級(也包括垃圾郵件發送者發送垃圾郵件與用戶進行搜尋引擎優化)，以及其他需要分析許多對象之間關係的地方。連結也取決於兩個節點時間行為的相似性。例如，氣候網絡中兩個地點(節點)之間的聯繫是由兩個地點的降雨或溫度變化的相似性決定的。[16][17][18]
對網絡結構魯棒性的研究利用了滲流理論。[19]當節點(或連結)的關鍵部分被刪除時，網絡就會分裂成小的、不連通的社團。這種現象被稱為滲流現象，它代表了臨界指數從有序到無序的一種相變類型。[20]滲流理論可以預測最大連通分量(稱為超連通分量)的大小、臨界滲流閾值和臨界指數。其中一個例子是利用滲透理論預測生物病毒殼層(衣殼)的破碎，並通過實驗預測並檢測乙肝病毒衣殼的滲透閾值:在底邊為菱形的範圍上隨機進行分子量級的堆疊遊戲。[21][22]
一些網絡搜索排名算法使用了以連結為中心的衡量指標，包括谷歌的PageRank、Kleinberg的HITS算法、CheiRank和TrustRank算法。連結分析也應用於信息科學和通信科學中，從而了解並提取網頁結構中的信息。例如，有可能是針對政治家的網站或博客之間相互聯繫的分析。另一個用途是根據在其他頁面中提到的內容對頁面進行分類。[23]
圖中節點和邊的相對重要性的信息可以通過中心性的測量得出，其社會學等學科中得到廣泛應用。例如，特徵向量中心性利用鄰接矩陣針對該網絡的特徵向量來確定有被頻繁訪問趨勢的節點。正式建立的中心性指標有度中心性、接近中心性、介數中心性、特徵向量中心性、子圖中心性和Katz中心性。分析的目的或目標通常由使用的中心性測量類型所決定。例如，如果一個人對網絡動態或網絡在移除節點/邊時的魯棒性感興趣，通常節點的動態重要性是中心度測量中最相關的參數。[24]基於k-core分析的中心性測量見參考文獻。[25]
這些概念用於描述網絡中集線器的連結偏好。集線器是具有大量連接的節點。一些集線器傾向於連接到其他集線器，而另一些集線器則避免連接到集線器而傾向於連接到連接性較差的節點。當一個集線器傾向於連接到其他集線器時，其被稱為同型集線器。異型集線器則避免連接到其他集線器。如果集線器是處於預期隨機概率的則稱為中性。有三種方法可以量化其相關性程度。
遞歸圖的遞歸矩陣可以看作是無向無權網絡的鄰接矩陣。這允許通過網絡標準對時間序列進行分析。其應用範圍為檢測從特徵動力學到同步分析的狀態變化。[26][27][28]
在複雜網絡中的內容可以通過兩種主要方式傳播:守恆傳播與不守恆傳播。[29]在守恆傳播中，進入複雜網絡的內容總量在其通過時保持不變。這種守恆傳播模型可以用一個裝有水的水罐被倒入由管道連接的漏斗來表示。其中水罐代表源頭，水則是正在傳播的內容。漏斗和連接管道分別表示節點與這些節點之間的連接。當水從一個漏斗流到另一個漏斗時，先前漏斗中的水會立即消失。在不守恆傳播中，內容的數量在其進入和通過複雜網絡時發生變化。不守恆傳播模型可以用一個連續運行且通過由管道連接的漏斗的水龍頭來表示。其中來自水源的水量是無限的。同時，任何接觸過水的漏斗，即時在水進入下一個漏斗時，也會繼續受到水的影響。不守恆模型非常適用於解釋大多數傳染病、神經興奮、信息和謠言等的傳播。
相互依賴網絡是一個耦合網絡系統，其中一個或多個網絡的節點取決於其他網絡中的節點。現代技術的發展增強了這種依賴性。依賴關係可能導致網絡之間的級聯故障，一個相對較小的失誤便可能導致系統的災難性故障。停電是網絡之間的依賴性重要地位的一個有代表性的證明。最近的一項研究開發了一個框架來研究相互依賴的網絡系統中的級聯故障。[30][31]
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
