非慣性參考系

在牛頓力學中，非慣性參考系是指在僅考慮實際力（而非虛擬力）時，不遵守牛頓運動定律的參考系。給定一個慣性參考系，當第二個參考系相對於第一個參考系描述了一個加速運動時，第二個參考系便是非慣性的。非慣性參考系的加速度可以由以下原因引起：

• 其平移速度的大小發生變化（線性加速度）。
• 其平移速度的方向發生變化（例如圍繞慣性參考系的旋轉運動）。
• 自身的旋轉運動（見圖1）。
• 上述幾種情況的組合。

圖 1 .相對於另一個參考系（S）旋轉的參考系 (S')

例如，地球上固定坐標系中的非慣性參考系可以視作一個例子，在該參考系中，物體的運動是相對於地球表面上正在旋轉的點進行測量的。

位於非慣性參考系中的觀察者需要引入虛擬力（例如科里奧利力或離心力）來解釋相對於該參考系的運動。這些力並非真正存在，因為它們並非由與其他物體的相互作用直接引起，但為了根據牛頓定律解釋現象，必須引入這些力。

因此，可以通過觀察一個參考系是否違反牛頓定律來判斷它是否是非慣性的。例如，地球自轉通過傅科擺上引力矢量的旋轉表現出來，導致擺的擺動平面相對於周圍環境發生變化。

嚴格來說，可以認為慣性參考系並不存在，或者至少在我們的環境中並不存在，因為地球既繞自轉軸自轉，又繞太陽運動，而太陽又繞銀河系中心運動。然而，為了簡化問題，通常我們會將實際並非慣性參考系的系統視作慣性參考系，只要所犯的誤差在可接受範圍內。因此，對於許多問題來說，通常會將地球表面視為慣性參考系。

非慣性參考系的示例

示例 1：圓周運動

圖2 .圓周運動

考慮一個以角速度${\displaystyle {\vec {\omega }}}$旋轉的旋轉平台，如圖2所示。

位於非慣性參考系（O'，x'，y'，z'）中的觀察者會發現，物體趨向於平台的外側，沿徑向方向運動。為了使物體保持在平台上，觀察者將物體用繩子固定在平台中心的垂直杆上。觀察者測量繩子的張力（圖2中的T），並通過一股與張力大小相同但方向相反的力來解釋該張力，這股力即為離心力（圖2中的${\displaystyle F_{f}}$）。

然而，對於位於慣性參考系（O，x，y，z）中的觀察者，物體在平台上的運動僅受繩子的張力影響（假設沒有與平台的摩擦力）。繩子的張力提供了向心加速度（大小為${\displaystyle \omega ^{2}\cdot R}$），使得物體沿圓周軌跡運動，而不是沿直線運動，這符合牛頓定律。

因此，只有位於非慣性參考系中的觀察者需要引入虛擬力來解釋物體的運動。

示例 2：電梯

圖3 .參考系（O, x, y）將被視為慣性參考系，而（O, x', y'）將被視為非慣性參考系。

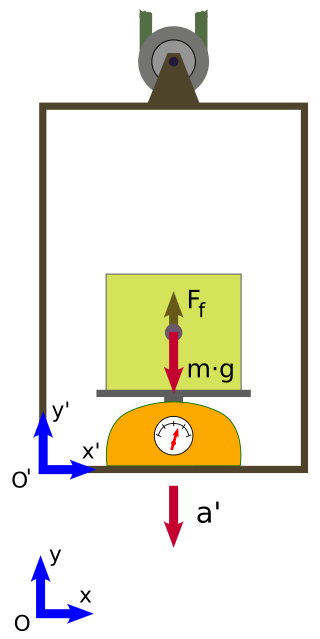
假設一個電梯以加速度a′（${\displaystyle a'<g}$）下降，如圖3所示，且參考係為慣性參考系。位於電梯內部的觀察者沒有外部參考點，會認為自己處在地球重力場中的慣性參考系內。觀察者放下一個質量為 ${\displaystyle m}$的物體，從高度${\displaystyle h}$處自由下落，並在電梯內的參考系中觀察物體的運動。

觀察者假設物體僅受到重力加速度的影響，因此物體的位置將是時間的函數，按照勻加速運動的公式給出：

${\displaystyle y_{m}=h-{\frac {1}{2}}\,g\,t^{2}}$

當物體到達電梯地板時（y=0）：

${\displaystyle 0=h-{\frac {1}{2}}\,g\,t^{2}}$

由此可以得到物體下落所需的時間：

${\displaystyle t={\sqrt {\frac {2h}{g}}}}$

然而，觀察者測量的時間比上述公式給出的時間要長。因此，物體的加速度必須小於重力加速度。為了說明這一點，觀察者認為一定有另一種力（虛擬力）與物體的運動相對抗，因此：

${\displaystyle P-F_{f}=m\cdot a\Rightarrow m\cdot g-m\cdot a'=m\cdot a\Rightarrow g-a'=a}$

其中${\displaystyle a}$為觀察者所測得的物體加速度。 因此，正確的時間表達式應為：

${\displaystyle t={\sqrt {\frac {2h}{(g-a')}}}}$

圖4 .電梯加速度的影響使得物體的重力表現為比實際重力更小的值。

對於位於慣性參考系中的觀察者，則不需要引入任何虛擬力來解釋物體的運動。電梯地板的位置為：

${\displaystyle y_{a}=y_{o}-{\frac {1}{2}}\,a'\,t^{2}}$

物體的位置為：

${\displaystyle y_{m}=y_{o}+h-{\frac {1}{2}}\,g\,t^{2}}$

當物體到達電梯地板時，物體的位置和電梯地板的位置重合，${\displaystyle y_{a}=y_{m}}$，因此有：

${\displaystyle y_{o}-{\frac {1}{2}}\,a'\,t^{2}=y_{o}+h-{\frac {1}{2}}\,g\,t^{2}\Rightarrow 0=h-{\frac {1}{2}}\,(g-a')\,t^{2}}$

由此得出：

${\displaystyle t={\sqrt {\frac {2h}{(g-a')}}}}$

這一表達式與在非慣性參考系中使用虛擬力所得到的時間一致。 此外，如果將已知質量放置在電梯地板上的秤上，觀察者會發現天平顯示的重量小於物體的實際重量。天平測得的物體的「表觀重量」將是物體真實重量減去虛擬力（如圖4所示）。即：

${\displaystyle P_{a}=P_{r}-F_{f}=m\cdot g-m\cdot a'=m\cdot (g-a')=m\cdot a}$

類似的推理可以應用於電梯${\displaystyle a'}$上升的情況，唯一的區別是虛擬力的方向與下降時相反，指向下方。

牛頓力學中的形式推導

圖5 .參考系

設S和S'是如圖5所示的兩個參考系。假設S是一個固定的參考系，而S'是一個相對於S具有加速度的非慣性參考系（包括平移和/或旋轉）。

可以證明，任意向量${\displaystyle \,{\vec {b}}\,}$在這兩個參考系S和S'中的時間導數之間，通過以下公式相關：

${\displaystyle \left[{\frac {d{\vec {b}}}{dt}}\right]_{S}=\left[{\frac {d{\vec {b}}}{dt}}\right]_{S'}+{\vec {\omega }}_{S'|S}\times {\vec {b}}}$（1）

S'的下標表示對哪個參考系進行導數運算，${\displaystyle {\vec {\omega }}_{S'|S}}$是參考系S'相對於參考系S的角速度。

公式（1）將幫助我們推導出關於非慣性參考系S'的牛頓第二定律。接下來我們將進行這個推導。

圖6 .物體在兩個參考系中的位置

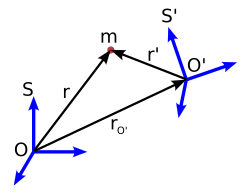
設質量為m的物體，分別位於參考系S和S'中，如圖6所示。位置矢量之間通過以下方程關聯：

${\displaystyle {\vec {r}}={\vec {r\,'}}+{\vec {r}}_{O'}}$ (2)

對方程（2）關於時間求導並應用公式（1），我們得到：

${\displaystyle \left[{\frac {d{\vec {r}}}{dt}}\right]_{S}=\left[{\frac {d{\vec {r\,'}}}{dt}}\right]_{S}+\left[{\frac {d{\vec {r}}_{O'}}{dt}}\right]_{S}=\left[{\frac {d{\vec {r\,'}}}{dt}}\right]_{S'}+{\vec {\omega }}_{S'|S}\times {\vec {r\,'}}+\left[{\frac {d{\vec {r}}_{O'}}{dt}}\right]_{S}}$

該式也可以寫為速度之間的關係：

${\displaystyle {\vec {v}}={\vec {v\,'}}+{\vec {\omega }}_{S'|S}\times {\vec {r\,'}}+{\vec {v}}_{O'}}$ (4)

繼續對其進行求導，並再次應用公式（1），我們得到：

${\displaystyle \left[{\frac {d{\vec {v}}}{dt}}\right]_{S}=\left[{\frac {d{\vec {v\,'}}}{dt}}\right]_{S}+\;{\frac {d{\vec {\omega }}_{S'|S}}{dt}}\times {\vec {r\,'}}\;+\;{\vec {\omega }}_{S'|S}\times \left[{\frac {d{\vec {r\,'}}}{dt}}\right]_{S}+\left[{\frac {d{\vec {v}}_{O'}}{dt}}\right]_{S}}$${\displaystyle =\left[{\frac {d{\vec {v\,'}}}{dt}}\right]_{S'}+\;{\vec {\omega }}_{S'|S}\times {\vec {v\,'}}\;+\;{\frac {d{\vec {\omega }}_{S'|S}}{dt}}\times {\vec {r\,'}}\;+\;{\vec {\omega }}_{S'|S}\times \left(\left[{\frac {d{\vec {r\,'}}}{dt}}\right]_{S'}+{\vec {\omega }}_{S'|S}\times {\vec {r\,'}}\right)+\left[{\frac {d{\vec {v}}_{O'}}{dt}}\right]_{S}}$

該式可重寫為：

${\displaystyle {\vec {a}}={\vec {a\,'}}+2\;{\vec {\omega }}_{S'|S}\times {\vec {v\,'}}+{\vec {\alpha }}\times {\vec {r\,'}}+{\vec {\omega }}_{S'|S}\times \left({\vec {\omega }}_{S'|S}\times {\vec {r\,'}}\right)+{\vec {a}}_{O'}}$

由此，非慣性參考系中物體的加速度為：

${\displaystyle {\vec {a\,'}}={\vec {a}}-2\;{\vec {\omega }}_{S'|S}\times {\vec {v\,'}}-{\vec {\alpha }}\times {\vec {r\,'}}-{\vec {\omega }}_{S'|S}\times \left({\vec {\omega }}_{S'|S}\times {\vec {r\,'}}\right)-{\vec {a}}_{O'}}$ (5)

通過質量乘積，最終得到非慣性參考系中的牛頓第二定律：

${\displaystyle {\vec {F'}}=m{\vec {a\,'}}=m{\vec {a}}-2m\;{\vec {\omega }}_{S'|S}\times {\vec {v\,'}}-m{\vec {\omega }}_{S'|S}\times \left({\vec {\omega }}_{S'|S}\times {\vec {r\,'}}\right)-m{\vec {\alpha }}\times {\vec {r\,'}}-m{\vec {a}}_{O'}}$ (6)

另一方面，慣性參考系中的牛頓第二定律為：

${\displaystyle {\vec {F}}=m{\vec {a}}}$ (7)

比較公式（6）和（7）可見，在非慣性參考系中出現了四個項，這些項被稱為虛擬力，因為它們並不是由物體與其他物體的相互作用引起的：

1. ${\displaystyle -2m\;{\vec {\omega }}_{S'|S}\times {\vec {v\,'}}}$稱為科里奧利力。
2. ${\displaystyle -m{\vec {\omega }}_{S'|S}\times \left({\vec {\omega }}_{S'|S}\times {\vec {r\,'}}\right)}$稱為離心力。
3. ${\displaystyle -m{\vec {\alpha }}\times {\vec {r\,'}}}$是一種僅在具有角加速度的系統中出現的力。
4. ${\displaystyle -m{\vec {a}}_{O'}}$是由S'的原點相對於S的加速度引起。

這四個項的符號均為負，表示這些加速度是對應於以 O' 為中心的S'系統相對於以 O 為中心的慣性參考系S所受的加速度。虛擬力補償了這些加速度，確保S'相對於S的加速度。

相對論力學中的形式推導

相對論力學考慮在平坦時空或閔考斯基時空中運動的機械系統。在該理論中，任何可接受的坐標系都是有效的來表示運動。

然而，牛頓定律的簡單推廣在這些坐標系中並不適用，除非它們是伽利略坐標系，其中克里斯托費爾符號為零。對於任意參考系，相對論中的牛頓第二定律的等效形式為：

${\displaystyle m\left({\frac {d^{2}x^{\mu }}{d\tau ^{2}}}+\sum _{\sigma ,\nu }\Gamma _{\sigma \nu }^{\mu }{\frac {dx^{\sigma }}{d\tau }}{\frac {dx^{\nu }}{d\tau }}\right)=F^{\mu },}$

其中：

${\displaystyle m\,}$是粒子的質量，

${\displaystyle x^{\mu }\,}$是粒子的坐標，

${\displaystyle \tau \,}$是粒子的原時，

${\displaystyle \Gamma _{\sigma \nu }^{\mu }\,}$是與坐標系統相關的克里斯托費爾符號，

${\displaystyle F^{\mu }\,}$是作用在粒子上的四維矢量。

在慣性參考系中，由於${\displaystyle \Gamma _{\sigma \nu }^{\mu }=0}$，得到：

${\displaystyle m{\frac {d^{2}x^{\mu }}{d\tau ^{2}}}=F^{\mu },}$

這與牛頓第二定律的形式相同。

參見

• 參考系
• 慣性參考系
• 虛擬力

參考

外部連結

• 參考系統的問題。曼努埃爾·阿隆索·桑切斯

高級水平

• 經典力學。卡耶塔諾·迪·巴托洛。
• 經典力學筆記。巴爾塞羅研究所。