在幾何學中，等邊或稱邊可遞是指所有邊都相等的幾何圖形，同時其對稱性可以在其邊上遞移。通俗地說，這意味着這個幾何結構中只有一種類型的邊，同時在這個立體上任選兩個邊，並透過平移、旋轉或鏡射等變換將一邊變換到另一個邊的位置時，其仍佔有相同的空間區域。
邊可遞多邊形
邊可遞多邊形是偶數邊數的等邊多邊形。並非所有等邊多邊形都是邊可遞多邊形。邊可遞多邊形的對偶多邊形是等角多邊形。[1]
通常邊可遞2n邊形具有Dn (*nn)的二面體群對稱性。[2]例如菱形是一種邊可遞多邊形，並具備D2 (*22)的二面體群對稱性。[2]所有正多邊形都是邊可遞多邊形[3]:48，並具有2倍的最小對稱性階數：正n邊形具有Dn (*nn)的二面體群對稱性。
邊可遞2n邊形可以用符號{nα}來表示，其中α代表最外側的內角。第二外側的內角β可能大於或小於180度。星形多邊形也可以是邊可遞多邊形，其可以用符號{(n/q)α}來表示，其中q<n-1且n和q互質（gcd(n,q)=1），而q代表轉數或密度[4]。
| 邊數 （2n） | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
|---|---|---|---|---|---|---|---|
| {nα} 凸 β<180 凹 β>180 |
 {2α} |
  {3α} |
  {4α} |
  {5α} |
  {6α} |
  {7α} |
  {8α} |
| 2轉 {(n/2)α} |
-- |  {(3/2)α} |
 2{2α} |
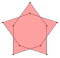  {(5/2)α} |
  2{3α} |
  {(7/2)α} |
  2{4α} |
| 3轉 {(n/3)α} |
-- | -- |  {(4/3)α} |
 {(5/3)α} |
 3{2α} |
  {(7/3)α} |
  {(8/3)α} |
| 4轉 {(n/4)α} |
-- | -- | -- |  {(5/4)α} |
 2{(3/2)α} |
 {(7/4)α} |
 4{2α} |
| 5轉 {(n/5)α} |
-- | -- | -- | -- |  {(6/5)α} |
 {(7/5)α} |
 {(8/5)α} |
| 6轉 {(n/6)α} |
-- | -- | -- | -- | -- |  {(7/6)α} |
 2{(4/3)α} |
| 7轉 {(n/7)α} |
-- | -- | -- | -- | -- | -- |  {(8/7)α} |
邊可遞多面體與鑲嵌
所有正多面體都具備等面（面可遞）、等邊（邊可遞）和等角（點可遞）的特性[5]。
擬正多面體或擬正鑲嵌圖，例如截半立方體和截半二十面體，其同時具備了等角（點可遞）與等邊（邊可遞）的特性，但不具備等面（面可遞）的特性。[6][7]其對偶多面體，如菱形十二面體和菱形三十面體具備等面與等邊的特性，而不具備等角的特性。
並非所有由正多邊形組成的多面體或鑲嵌都是邊可遞的，就算他所有邊都等長，也可能因為邊的相鄰面不同（稜的組成不同）而導致其不滿足邊可遞的特性。例如截角二十面體（足球的形狀）就不滿足邊可遞的特性，因為它具有兩種類型的邊：六邊形-六邊形公共邊和六邊形-五邊形公共邊，並且立體的對稱性不允許將六邊形-六邊形邊移動到六邊形-五邊形邊。
邊可遞多面體所有稜的二面角皆相等。
凸多面體的對偶多面體仍為凸多面體[8]；非凸多面體的對偶多面體也仍為非凸多面體[8]；邊可遞多面體的對偶多面體亦仍為邊可遞多面體。
參見
參考文獻
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
