抛物面
来自维基百科,自由的百科全书
抛物面(英文:Paraboloid)是二次曲面的一种。抛物面有两种:椭圆抛物面和双曲抛物面。椭圆抛物面在笛卡儿坐标系中的方程为:


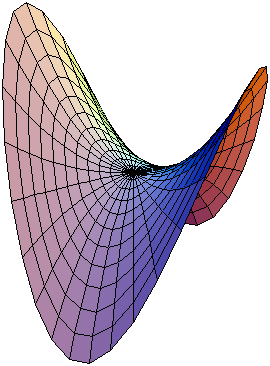
双曲抛物面在笛卡儿坐标系中的方程为:
性质
当a = b时,曲面称为旋转抛物面,它可以由抛物线绕着它的轴旋转而成。它是抛物面反射器的形状,把光源放在焦点上,经镜面反射后,会形成一束平行的光线。反过来也成立,一束平行的光线照向镜面后,会聚集在焦点上。
曲率
椭圆抛物面的参数方程为:
高斯曲率为:
平均曲率为:
它们都是正数,在顶点处最大,越远离顶点曲率越小,并趋近于零。
双曲抛物面的参数方程为:
高斯曲率为:
平均曲率为:
乘法表
如果把双曲抛物面
顺着+z的方向旋转π/4的角度,则方程为:
如果,则简化为:
- .
最后,设,我们可以看到双曲抛物面
- .
与以下的曲面是全等的:
因此它可以视为乘法表的几何表示。
两个函数
和
它是函数的解析延拓。
参见
参考文献
- Beyer, W. H. (Ed.). CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 133, 1987.
- Gray, A. "The Paraboloid." §13.5 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 307-308, 1997.
- Harris, J. W. and Stocker, H. "Paraboloid of Revolution." §4.10.2 in Handbook of Mathematics and Computational Science. New York: Springer-Verlag, p. 112, 1998.
- Hilbert, D. and Cohn-Vossen, S. Geometry and the Imagination. New York: Chelsea, pp. 10-11, 1999.
- Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, 1999.
Wikiwand - on
Seamless Wikipedia browsing. On steroids.