度數矩陣

在數學領域圖論中，無向圖的度數矩陣（英語：degree matrix）是一個對角矩陣 ，其中包含的信息為的每一個頂點的度數，也就是每個頂點相鄰的邊數。^[1] 它可以和鄰接矩陣一起使用以構造圖的拉普拉斯算子矩陣（拉普拉斯矩陣是度數矩陣和鄰接矩陣的差值）。^[2]

定義

給定一個圖 ${\displaystyle G=(V,E)}$ 與 ${\displaystyle |V|=n}$， ${\displaystyle G}$的度數矩陣 ${\displaystyle D}$是一個 ${\displaystyle n\times n}$的對角線矩陣，其定義為^[1]

${\displaystyle d_{i,j}:=\left\{{\begin{matrix}\deg(v_{i})&{\mbox{if}}\ i=j\\0&{\mbox{otherwise}}\end{matrix}}\right.}$

其中度數 ${\displaystyle \deg(v_{i})}$為這個頂點上的邊的條數。 在無向圖中，這意味着每個環會使得度數增加2。 在有向圖中，術語「度」可以指「入度」（indegree，終點在這個頂點的邊的條數）或「出度」（ outdegree，起點在這個頂點的邊的條數）。

例子

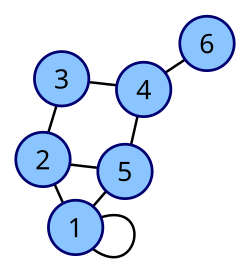
下面的無向圖有一個6x6的度數矩陣，其數值為。

Vertex labeled graph	度數矩陣
	${\displaystyle {\begin{pmatrix}4&0&0&0&0&0\\0&3&0&0&0&0\\0&0&2&0&0&0\\0&0&0&3&0&0\\0&0&0&0&3&0\\0&0&0&0&0&1\\\end{pmatrix}}}$

注意，對於無向圖而言，開始和結束於同一節點的邊（即環，如上圖中的節點1）會使相應的度增加2（即被計算兩次）。

性質

一個k-正則圖的度數矩陣是恆為${\displaystyle k}$的對角線矩陣。

根據度的總和公式，度數矩陣的跡是對應圖的邊數的兩倍。

參考文獻

1. Chung, Fan; Lu, Linyuan; Vu, Van, Spectra of random graphs with given expected degrees, Proceedings of the National Academy of Sciences of the United States of America, 2003, 100 (11): 6313–6318, MR 1982145, PMC 164443 , PMID 12743375, doi:10.1073/pnas.0937490100
2. Mohar, Bojan, Graph Laplacians, Beineke, Lowell W.; Wilson, Robin J. (編), Topics in algebraic graph theory, Encyclopedia of Mathematics and its Applications 102, Cambridge University Press, Cambridge: 113–136, 2004, ISBN 0-521-80197-4, MR 2125091.