多貝西小波

多貝西小波（英語：Daubechies Wavelet），是以比利時女性物理暨數學家英格麗·多貝西（Ingrid Daubechies）的名字命名之一種小波函數，當初英格麗·多貝西發現了一種具有階層（hierarchy）性質的小波，便將此小波以她的名字命名。多貝西小波主要應用在離散型的小波轉換，是最常使用到的小波轉換，通常使用在數位信號分析、信號壓縮跟雜訊去除。

一般而言的離散小波轉換通常是以正交小波（orthogonal wavelet）為基底，而多貝西小波也是一種正交小波。由於它很容易經由快速小波轉換（fast wavelet transform（FWT））實現，所以常會放在數位信號處理的教科書中教學。

對於有限長度的小波，應用於快速小波轉換（fast wavelet transform（FWT））時，會有兩個實數組成的數列：一是作為高通濾波器的系數，稱作小波濾波器（wavelet filter,也稱為mother wavelet）；二是低通濾波器的系數，稱作調整濾波器（scaling filter,也稱為father wavelet）。

我們則以濾波器的長度N來形容濾波器為DN，例如：N=2的多貝西小波寫作D2、N=4的多貝西小波寫作D4，以此類推（N為偶數）。實際上常用的多貝西小波為D2到D20。與之對應的另一種描述方式是db N，其中N指消失矩的數量，由此，D4和db2是同一種多貝西小波。

性質

• 分類方式

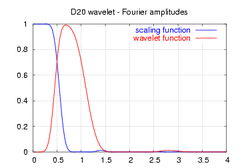
  多貝西小波的分類是以消失動量（vanishing moment）的值A（亦為消失動量的個數）為依據（A稱為tap），調整函式（scaling function）及小波函式（wavelet function）的平滑度（smoothness）皆會隨着消失動量的值（tap）增加而增加：例如，當A=1時，多貝西小波即是哈爾小波（Haar wavelet），調整函式及小波函式都是不連續的；當A=2時，多貝西小波的調整函式及小波函式為不能平滑微分的連續函式；當A=3時，調整函式及小波函式已經是連續可微的函式了。以此類推，當A愈大時，多貝西小波的兩個函式平滑度會愈來愈高。以下為多貝西小波跟不同A的調整及小波函式圖：

尺度函數（藍色）和小波函數（紅色）
對應函數的頻譜幅度

• 長度

  多貝西小波的長度為消失動量（vanishing moment）值A的兩倍；所以當消失動量為A時，多貝西小波的小波濾波器（wavelet filter）及調整濾波器（scaling filter）長度皆為2A（N=2A）。一般而言，我們仍是以N來形容多貝西小波的長度：例如，當A=1時，有一個消失動量，多貝西小波寫成D2，長度為2（也是Haar小波）；當A=2時，有兩個消失動量，多貝西小波寫成D4，長度為4；以此類推。但是，在MATLAB的使用上是以dbA描述多貝西小波，以下則為調整濾波器的系數及A的關係表：

正交多貝西小波系數

Scaling Coefficient ${\displaystyle p_{k}}$	db1（Haar）	db2	db3	db4	db5	db6	db7	db8	db9	db10
${\displaystyle p_{0}}$	1	0.6830127	0.47046721	0.32580343	0.22641898	0.15774243	0.11009943	0.07695562	0.05385035	0.03771716
${\displaystyle p_{1}}$	1	1.1830127	1.14111692	1.01094572	0.85394354	0.69950381	0.56079128	0.44246725	0.34483430	0.26612218
${\displaystyle p_{2}}$		0.3169873	0.650365	0.8922014	1.02432694	1.06226376	1.03114849	0.95548615	0.85534906	0.74557507
${\displaystyle p_{3}}$		-0.1830127	-0.19093442	-0.03957503	0.19576696	0.44583132	0.66437248	0.82781653	0.92954571	0.97362811
${\displaystyle p_{4}}$			-0.12083221	-0.26450717	-0.34265671	-0.31998660	-0.20351382	-0.02238574	0.18836955	0.39763774
${\displaystyle p_{5}}$			0.0498175	0.0436163	-0.04560113	-0.18351806	-0.31683501	-0.40165863	-0.41475176	-0.35333620
${\displaystyle p_{6}}$				0.0465036	0.10970265	0.13788809	0.1008467	6.68194092e-4	-0.13695355	-0.27710988
${\displaystyle p_{7}}$				-0.01498699	-0.00882680	0.03892321	0.11400345	0.18207636	0.21006834	0.18012745
${\displaystyle p_{8}}$					-0.01779187	-0.04466375	-0.05378245	-0.02456390	0.043452675	0.13160299
${\displaystyle p_{9}}$					4.71742793e-3	7.83251152e-4	-0.02343994	-0.06235021	-0.09564726	-0.10096657
${\displaystyle p_{10}}$						6.75606236e-3	0.01774979	0.01977216	3.54892813e-4	-0.04165925
${\displaystyle p_{11}}$						-1.52353381e-3	6.07514995e-4	0.01236884	0.03162417	0.04696981
${\displaystyle p_{12}}$							-2.54790472e-3	-6.88771926e-3	-6.67962023e-3	5.10043697e-3
${\displaystyle p_{13}}$							5.00226853e-4	-5.54004549e-4	-6.05496058e-3	-0.01517900
${\displaystyle p_{14}}$								9.55229711e-4	2.61296728e-3	1.97332536e-3
${\displaystyle p_{15}}$								-1.66137261e-4	3.25814671e-4	2.81768659e-3
${\displaystyle p_{16}}$									-3.56329759e-4	-9.69947840e-4
${\displaystyle p_{17}}$									-5.5645514e-5	-1.64709006e-4
${\displaystyle p_{18}}$										1.32354367e-4
${\displaystyle p_{19}}$										-1.875841e-5

Coiflet filter ${\displaystyle g_{k},h_{k}}$	0	1	2	3	4	5	6	7	8	9
${\displaystyle h_{4}}$	0.4829629131445	0.836516303	0.22414386	-0.129409522
${\displaystyle g_{4}}$	-0.129409522551	-0.22414386	0.83651630	-0.482962913
${\displaystyle h_{6}}$	0.3326705529500	0.80689150	0.45987750	-0.135011020	-0.08544127	0.03522629
${\displaystyle g_{6}}$	0.0352262918857	0.08544127	-0.13501102	-0.459877502	0.806891509	-0.33267055
${\displaystyle h_{8}}$	0.2303778133088	0.71484657	0.63088076	-0.027983769	-0.187034811	0.030841381	0.032883011	-0.0105974017
${\displaystyle g_{8}}$	-0.0105974017850	-0.03288301	0.03084138	0.1870348117	-0.027983769	-0.630880767	0.714846570	-0.2303778133
${\displaystyle h_{10}}$	0.1601023979741	0.60382926	0.72430852	0.1384281459	-0.242294887	-0.032244869	0.077571493	-0.0062414902	-0.012580751	0.003335725
${\displaystyle g_{10}}$	0.0033357252854	0.012580751	-0.0062414	-0.077571493	-0.032244869	0.2422948870	0.138428145	-0.7243085284	0.6038292697	-0.16010239

• 濾波器

這邊列出4到10點的filter，這些在實務上已經很夠用，消失點(vanish moment)也就是k/2。

g會是低頻的濾波器，h會是高頻的濾波器。

可以看出${\displaystyle h[n]=(-1)^{n}g[-n]}$，這邊採用python的語法，h會是g的反序，且n為基數時要乘上-1。

建立

多貝西小波具有調整函式（低通濾波）及小波函式（高通濾波）兩個函式。因此，我們需先建立調整函式及小波函式的系數:

首先，調整函數在多尺度分析（multi-resolution analysis）中的每一層皆可寫為下列方程式：

${\displaystyle \phi (x)=\sum _{k=0}^{N-1}a_{k}\phi (2x-k)}$,

其中${\displaystyle (a_{0},\dots ,a_{N-1})}$為有限長度實數數列，稱作調整系數。同時，小波函數也可以調整函數的線性組合表示：

${\displaystyle \psi (x)=\sum _{k=0}^{M-1}b_{k}\phi (2x-k)}$,

其中${\displaystyle (b_{0},\dots ,b_{M-1})}$亦為有限長度的實數數列，稱做小波系數。

因為上述方程式必須是齊性的（homogeneous），在建立上，這兩個函式會正規化（normalize）為和（sum）及平方和（sum of square）皆是2。

• 正交小波

  正交性質在此指調整系數就必須和位移偶數間隔後的調整系數互相垂直（內積為0），即為下式：

  ${\displaystyle \sum _{n\in \mathbb {Z} }a_{n}a_{n+2m}=2\delta _{m,0}}$.

• 由於正交的特性，小波系數會滿足下列條件：

  ${\displaystyle b_{n}=(-1)^{n}a_{N-1-n}}$, .

• 消失動量及多項式估計

  常用的多貝西小波為D2到D20，由於多貝西小波的消失動量為有限個，所以調整及小波系數可以表示為有限長度的多項式

  ${\displaystyle a[n]=a_{n}}$

• 上式經過Z轉換（Z-transform）後會變成：

  ${\displaystyle {A}(Z)=a_{0}+a_{1}Z+\dots +a_{N-1}Z^{N-1}}$,

• 我們可以將上式轉換為正交離散小波轉換的一般表示式

  ${\displaystyle a(Z)=2^{1-A}(1+Z)^{A}p(Z)}$, ${\displaystyle order=A}$，此時，${\displaystyle p(1)=1}$、${\displaystyle p}$有實系數及${\displaystyle deg(p)=A-1}$。

• 而正交的條件可寫成

  ${\displaystyle a(Z)\,a(Z^{-1})+a(-Z)\,a(-Z^{-1})=4}$,或是等同於${\displaystyle (2-X)^{A}P(X)+X^{A}\,P(2-X)=2^{A}\dots }$(#),

  ${\displaystyle X}$定義為可以產生對稱數列的勞倫茲多項式${\displaystyle X:=1/2\cdot (2-Z-Z^{-1})}$滿足${\displaystyle X(-Z)=2-X(Z)}$

• 因此${\displaystyle P(X)}$便成為對稱型勞倫滋多項式，即${\displaystyle P(X(Z))=P(Z)P(Z-1)}$。因為 ${\displaystyle X(e^{iw})=1-cos(w)}$及${\displaystyle p(e^{iw})p(e^{-iw})=|p(e^{iw})|^{2}}$, ${\displaystyle {P}}$則會是區段[0,2]中的非負實數。

• 方程式（#）如果除上${\displaystyle X}$的truncated power series則可求得對於每個${\displaystyle A}$的最小解

  ${\displaystyle P_{A}(X)=\sum _{k=0}^{A-1}\left({{A+k-1} \atop {A-1}}\right)2^{-k}X^{k}}$.（明顯的值會是在（0,2）間的正數）

• 而（#）的齊性方程式是一個對於${\displaystyle x=1}$的反對稱方程式，因此可得一般解為${\displaystyle X^{A}(X-1)R((X-1)^{2})}$，此一般解有${\displaystyle R}$個多項式實系數。

  因此和為

  (sum)${\displaystyle P(X)=P_{A}(X)+X^{A}(X-1)R((X-1)^{2})}$

  ${\displaystyle {P}}$的值在區間[0,2]中並有界線（界線為${\displaystyle 4^{A-r}}$,）。為了將${\displaystyle r}$最大化的過程中會產生許多具有不等式條件的線性方程式。

  為了解出${\displaystyle P(X(Z))=P(Z)P(Z^{-1})}$的${\displaystyle P}$，這裏使用Fejer-Riesz-algorithm這個方法（此為頻譜分解的方法）。多項式${\displaystyle P(X)}$會因此分開成許多線性因子（linear factor）${\displaystyle P(X)=(X-\mu _{1})\dots (X-\mu _{N})}$,此時${\displaystyle N=A+1+2deg(R)}$。每一個線性因子代表可以分解成兩個線性因子的一個勞倫茲多項式${\displaystyle (X(Z)-\mu )=-{\frac {1}{2}}Z+1-\mu -{\frac {1}{2}}Z^{-1}}$，任選其中一個線性因子都可設為${\displaystyle p(Z)}$。所以${\displaystyle p(Z)}$會有2^N個可能的答案。為了極端相位的目的，挑選所有根都是在單位圓上或是在單位圓內複數根的${\displaystyle P(Z)}$。

演算法

以下為示範小波轉換應用於影像壓縮，壓縮後為原本圖片的四分之一。

假設輸入的圖片大小為M*N，讓圖片對高頻和低頻進行卷積運算。

對M的基數進行取樣，這個結果會讓兩個維度都變成(M/2)*N。

把低頻的圖片放在上面，高頻的放在下面，低頻的圖片會長的像原本的圖片，高頻的圖片會是只有灰色的圖片。

對新的圖片再進行高頻和低頻的卷積，這時變成M*(N/2)的大小，低頻放在左邊，高頻放在右邊，

最後可以看到[0:M/2, 0:N/2]就會是原本壓縮過後的圖片。

因小波轉換有良好的性質，經過多次壓縮還是能保有原本的資訊。也就是說可以修改以下的程式碼改成迴圈的方式，

進行多次小波轉換，經過類似的模式再使用多次的反小波轉換，還原出原本大小的圖片。

import numpy as np
def subsampling(x, d):
    if d == 1:
        y = x[::2, :]
    elif d == 2:
        y = x[:, ::2]
    return y

def upsampling(x, d):
    s = x.shape
    if d == 1:
        y = np.zeros((p * s[0], s[1]))
        y[::2, :] = x
    elif d == 2:
        y = np.zeros((s[0], p * s[1]))
        y[:, ::2] = x
    return y
    
def cconv(x, h, d):
    if d == 2:
        return np.transpose(cconv(np.transpose(x), h, 1))
    y = np.zeros(x.shape)
    p = len(h)
    pc = int(round( float((p - 1) / 2 )))
    for i in range(0, p):
        y = y + h[i] * np.roll(x, i - pc, axis=0)
    return y
    
def DWT(image, h, g): # discrete wavelet transformation
    fW = image.copy()
    j = int(np.log2(image.shape[0])-1)
    A = fW[:2**(j+1):,:2**(j+1):]
    Coarse = subsampling(cconv(A,h,1),1)
    Detail = subsampling(cconv(A,g,1),1)
    A = np.concatenate( (Coarse, Detail), axis=0 )
    Coarse = subsampling(cconv(A,h,2),2)
    Detail = subsampling(cconv(A,g,2),2)
    A = np.concatenate( (Coarse, Detail), axis=1 )
    fW[:2**(j+1):,:2**(j+1):] = A
    return fW
    
def iDWT(image, fW, h, g): #image is original, fW is after DWT of that.
    f1 = fW.copy()
    j = int(np.log2(image.shape[0])-1)
    A = f1[:2**(j+1):,:2**(j+1):]
    Coarse = A[:2**j:,:]
    Detail = A[2**j:2**(j+1):,:]
    h1 = h[::-1]
    g1 = g[::-1]
    Coarse = cconv(upsampling(Coarse,1),h1,1)
    Detail = cconv(upsampling(Detail,1),g1,1)
    A = Coarse + Detail
    Coarse = A[:,:2**j:]
    Detail = A[:,2**j:2**(j+1):]
    Coarse = cconv(upsampling(Coarse,2),h1,2)
    Detail = cconv(upsampling(Detail,2),g1,2)
    A = Coarse + Detail
    f1[:2**(j+1):,:2**(j+1):] = A
    return f1

參照

• 小波分析

參考資料

1. A first course in Wavelets with Fourier Analysis, A.Boggess, F.J. Narcowich, 2001