反距離加權
来自维基百科,自由的百科全书
反距離加權(英語:inverse distance weighting,IDW)是一種在有已知的離散數據點的情形下進行多元插值的確定性算法。賦給未知點的值是用已知點的值的加權平均數計算得出的。該算法也可在空間自相關分析(例如莫蘭指數)中用於構建空間權重矩陣。[1]
該方法的名稱來自其加權的方式:未知點到每個已知點的距離的倒數。
問題的定義
對於給定的離散數據點,我們希望以一個函數對研究區域進行插值:
其中是研究區域。
個已知數據點可以視為元組列表:
該函數應當是「平滑的」(連續且一次可微),確定的(),並滿足用戶對研究的現象的直觀預期。此外,該功能應能夠以合理成本在電腦應用上實現(如今,基本實現方法中可能會用到並行計算)。
謝潑德法(Shepard's method)
自1965年起,在哈佛計算機圖形和空間分析實驗室,各專業的科學家匯聚一堂,重新思考現在稱作「地理信息系統」的各種問題。[2]
實驗室工作的推動者霍華德·費舍爾(Howard Fisher)構思了一種改良的計算機繪圖程序:SYMAP,其設計伊始,費舍爾就希望對插值進行改進。他向哈佛大學新生展示了SYMAP的進展,而後許多新生參與了實驗室活動。一位大一新生唐納德·謝潑德(Donald Shepard)決定對SYMAP中的插值法進行大改,隨後發表了他1968年的著名論文。[3]
謝潑德的算法也受到William Warntz和實驗室其他從事空間分析工作的人的理論方法的影響。他用距離的指數進行了許多實驗,決定更接近重力模型(-2的指數)。謝潑德不僅實現了基本的反距離加權,還允許障礙(包括可滲透的和絕對的)插值。
其他研究機構此時也在研究插值,特別是堪薩斯大學及其SURFACE II計劃。但SYMAP的功能仍是最先進的,儘管是由本科生編寫的。
給定一組樣本點,反距離加權插值函數定義為:
其中
這是一個簡單的反距離加權函數,其定義由謝潑德提出,[3]x表示一個被插值點(未知點),xi表示一個節點(已知點),是從已知點xi到未知點x的給定距離(度規算符),N是插值中使用的已知點的總數,並且是一個正實數,稱為冪參數。
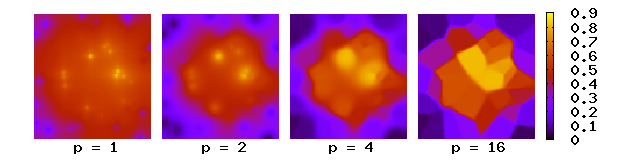
其中,權重隨着與已知點的距離的增加而減小。值越大,則最鄰近已知點的對插值的影響越大,當足夠大時,插值結果形似馬賽克多邊形(沃羅諾伊圖),每一個多邊形內的數值幾乎為恆定值。對於二維面,冪參數時,插值由距離較遠的點主導,因為密度為、鄰近節點距離為至之間的數據點集,權重的加和約為
其在且時發散。對於M維,同樣的結論適用於。對於值的選擇,可以考慮插值中所需的平滑程度、被插值的樣本密度和分佈,以及允許單個樣本影響周圍樣本的最大距離。
謝潑德法是最小化與插值點{x, u}的元組和插值點{xi, ui}的i元組之間的偏差度量相關的函數的結果,定義為:
從最小化條件導出:
該方法容易擴展到其他維數的空間,它實際上是將拉格朗日插值法推廣到多維空間。為三元插值設計的修改版算法由Robert J. Renka提出,Netlib的toms庫中的算法661提供該算法。

謝潑德法的另一個修改版是僅使用半徑R範圍內的最近鄰(而不是完整樣本)來計算插值。在這種情況下,權重略有修改:
當與快速空間搜索結構(如k-d樹)結合使用時,它即為適用於大尺度問題的高效N log N插值方法。
參見
參考文獻
Wikiwand - on
Seamless Wikipedia browsing. On steroids.




![{\displaystyle [(x_{1},u_{1}),(x_{2},u_{2}),...,(x_{N},u_{N})].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/639e496b90fb413c342ed159aad1f76d41278333)

















