在幾何學中，一個幾何圖形可分為凸或凹的。例如多邊形和多面體。其中，凸的多邊形稱為凸多邊形、凹的多邊形則可稱為凹多邊形或非凸多邊形，多面體與多胞體亦然。然而在三維或更高維度的空間中，不是凸的幾何圖形不一定會是凹幾何圖形，亦可能是星形幾何圖形，因此在三維或更高維度的空間中較常分為凸與非凸。
凸幾何圖形
凸幾何圖形是指內部為凸集的幾何圖形[1]，二維空間中的凸幾何圖形稱為凸多邊形、三維空間則稱凸多面體。若一多胞形的內部為凸集，則稱凸多胞形。
二維空間中的凸幾何圖形稱為凸多邊形，簡單多邊形的下列性質與其凸性等價：
凸幾何圖形的凸包與其邊界相同。
凹幾何圖形
凹幾何圖形是指內部不是凸集的幾何圖形，在二維空間中，不是凸集的簡單多邊形，稱為凹多邊形（Concave polygon）[2]或凹角[3]。
凹多邊形至少存在一個內角大於180度。
在三維空間中，不是凸的幾何圖形不一定會是凹幾何圖形，亦可能是星形多面體，因此在三維空間中較常分為凸與非凸。
-
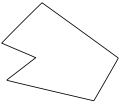
凹多邊形示例 -
凹多面體示例：凹鳶形柱 -
環形多面體
嚴格凸與非嚴格凸
如果一個簡單多邊形的每個內角嚴格小於180度，是嚴格凸的；如果每個非相鄰頂點間的線段除端點外嚴格位於多邊形的內部，也是嚴格凸的。
所有非退化三角形都是嚴格凸的。
星形幾何圖形
星形幾何圖形是非凸幾何圖形的一個特例，其並未有一個明確的定義。在二維空間中，稱為星形多邊形，數學家Branko Grünbaum指出了兩種由克普勒提出的定義：一種是具有自相交稜的正星形多邊形，且自相交的稜不產生新的頂點，另一種是邊可遞的簡單凹多邊形[4]。
參見
參考文獻
外部連結
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
