伽利略變換

伽利略變換（英語：Galilean transformation）是經典力學中用以在兩個只以勻速相對移動的參考系之間變換的方法，屬於一種被動態變換。在相對論效應下，伽利略變換在物體以接近光速運動時不成立^[1]，在電磁系統中也不會成立。^[2]

伽利略·伽利萊在解釋勻速運動時制定了這一套概念。^[3]他用其解釋球體滾下斜面這一力學問題，並測量出地球表面引力加速度的數值。

在狹義相對論中，伽利略變換被龐加萊變換所取代；相反，龐加萊變換的經典極限c →∞中的群收縮產生了伽利略變換。

平移

伽利略變換示意圖

伽利略變換建基於人們加減物體速度的直覺。在其核心，伽利略變換假設時間和空間是絕對的。

這項假設在洛倫茲變換中被捨棄，因此就算在相對論性速度下，洛倫茲變換也是成立的；而伽利略變換則是洛倫茲變換的低速近似值。

以下為伽利略變換的數學表達式，其中${\displaystyle (x,y,z,t)}$和${\displaystyle (x',y',z',t')}$分別為同一個事件在兩個坐標系${\displaystyle S}$和${\displaystyle S'}$中的坐標。兩個坐標系以相對勻速運行（速度為${\displaystyle v}$），運行方向為${\displaystyle x}$和${\displaystyle x'}$，原點在時間${\displaystyle t=t'=0}$時重合。 ^{[4] [5] [6] [7]}

${\displaystyle x'=x-vt\,}$

${\displaystyle y'=y\,}$

${\displaystyle z'=z\,}$

${\displaystyle t'=t\,}$

最後一條方程式意味着時間是不受觀測者的相對運動影響的。

利用線性代數的術語來說，這種變換是個錯切，是矩陣對向量進行變換的一個過程。當參考系只沿着x軸移動時，伽利略變換只作用於兩個分量：

${\displaystyle (x',t')=(x,t){\begin{pmatrix}1&0\\-v&1\end{pmatrix}}.}$

雖然在伽利略變換中沒有必要用到矩陣表達法，但是用了矩陣就可以和狹義相對論中的變換法進行比較。

三種伽利略變換

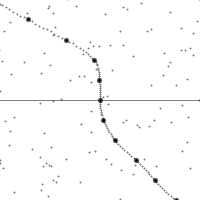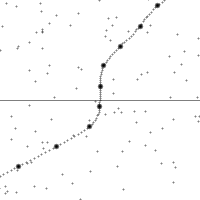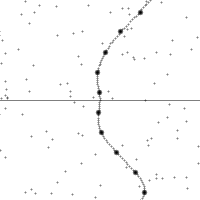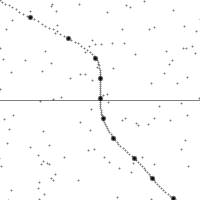
沿着一個加速中觀測者的世界線所看到的時空。

縱軸為時間，橫軸為距離，虛線為觀測者在時空中的軌跡。圖的下半部是已經發生了的事件，上半部則是未來的事件。圖中小點為時空中的事件。

世界線的斜率為觀測者的相對速率。注意觀測者在加速時所看到的時空會進行錯切。

伽利略變換可以唯一寫成由時空的旋轉、平移和勻速運動複合而成的函數。^[8]設x為三維空間中的一點，t為一維時間中的一點。時空當中的任何一點可以表達為有序對(x,t)。速度為v的勻速運動表達為${\displaystyle (\mathbf {x} ,t)\mapsto (\mathbf {x} +t\mathbf {v} ,t)}$，其中v在R³內。平移表達為${\displaystyle (\mathbf {x} ,t)\mapsto (\mathbf {x} +\mathbf {a} ,t+b)}$，其中a在R³內，b在R內。旋轉表達為${\displaystyle (\mathbf {x} ,t)\mapsto (G\mathbf {x} ,t)}$，其中G : R³ → R³為某正交變換。^[8]作為一個李群，伽利略變換的維度為10。^[8]

這三種變換可更加數學化地表達為伽利略群^[9]。首先G為SO(3)中的旋轉矩陣，3維內積在G的作用下保持不變，表達為:${\displaystyle <G{\overrightarrow {x}},G{\overrightarrow {y}}>=<{\overrightarrow {x}},{\overrightarrow {y}}>\,\!}$設在某t時刻有映射${\displaystyle \varphi _{t}({\overrightarrow {a}},{\overrightarrow {b}},G)}$將空間上的某一點x映射到另一點${\displaystyle G{\overrightarrow {x}}+{\overrightarrow {a}}+{\overrightarrow {b}}\cdot t}$上。可證得${\displaystyle \varphi _{t}}$構成一個群。
結合律：${\displaystyle \varphi _{t}}$為線性映射，線性映射滿足結合律。

單位元：${\displaystyle \varphi _{t}({\overrightarrow {0}},{\overrightarrow {0}},\mathbf {I} )({\overrightarrow {x}})={\overrightarrow {x}}}$

逆映射：${\displaystyle \varphi _{t}({\overrightarrow {a}},{\overrightarrow {b}},G)^{-1}=\varphi _{t}(-G^{-1}{\overrightarrow {a}},-G^{-1}{\overrightarrow {b}},G^{-1})}$

封閉性：${\displaystyle {\begin{aligned}\varphi _{t}({\overrightarrow {a'}},{\overrightarrow {b'}},G')\circ \varphi _{t}({\overrightarrow {a}},{\overrightarrow {b}},G)({\overrightarrow {x}})=GG'{\overrightarrow {x}}+(G'{\overrightarrow {a}}+{\overrightarrow {a'}})+(G{\overrightarrow {b}}+{\overrightarrow {b'}})\cdot t\\=\varphi _{t}(G'{\overrightarrow {a}}+{\overrightarrow {a'}},G{\overrightarrow {b}}+{\overrightarrow {b'}},GG')({\overrightarrow {x}})\end{aligned}}}$ 對應的有：
空間平移：${\displaystyle \varphi _{t}({\overrightarrow {a}},{\overrightarrow {0}},\mathbf {I} )({\overrightarrow {x}})={\overrightarrow {x}}+{\overrightarrow {a}}}$
速度變換：${\displaystyle \varphi _{t}({\overrightarrow {0}},{\overrightarrow {b}},\mathbf {I} )({\overrightarrow {x}})={\overrightarrow {x}}+{\overrightarrow {b}}\cdot t}$
空間旋轉：${\displaystyle \varphi _{t}({\overrightarrow {0}},{\overrightarrow {0}},G)({\overrightarrow {x}})=G{\overrightarrow {x}}}$
${\displaystyle \varphi _{t}({\overrightarrow {a}},{\overrightarrow {b}},G)}$為不含時伽利略群，加上時間平移${\displaystyle t\mapsto t+t_{0}}$後映射${\displaystyle ({\overrightarrow {x}},t)\mapsto (\varphi _{t},t+t_{0})=(G{\overrightarrow {x}}+{\overrightarrow {a}}+{\overrightarrow {b}}\cdot t,t+t_{0})}$構成一個完整伽利略群，其依舊滿足群的性質。完整伽利略群具有10個生成元，分別為3個空間平移(x,y,z)，3個空間轉動(對應3個坐標基矢），3個速度，以及一個時間平移。

伽利略群的中心擴張

這裏我們只考慮伽利略群的李代數。結果能夠輕易延伸到李群。L的李代數由H、P_i、C_i和L_ij張成（反對稱張量），並能夠受交換子的作用，其中

${\displaystyle [H,P_{i}]=0\,\!}$

${\displaystyle [P_{i},P_{j}]=0\,\!}$

${\displaystyle [L_{ij},H]=0\,\!}$

${\displaystyle [C_{i},C_{j}]=0\,\!}$

${\displaystyle [L_{ij},L_{kl}]=i[\delta _{ik}L_{jl}-\delta _{il}L_{jk}-\delta _{jk}L_{il}+\delta _{jl}L_{ik}]\,\!}$

${\displaystyle [L_{ij},P_{k}]=i[\delta _{ik}P_{j}-\delta _{jk}P_{i}]\,\!}$

${\displaystyle [L_{ij},C_{k}]=i[\delta _{ik}C_{j}-\delta _{jk}C_{i}]\,\!}$

${\displaystyle [C_{i},H]=iP_{i}\,\!}$

${\displaystyle [C_{i},P_{j}]=0\,\!.}$

H為時間平移的生成元（哈密頓算符），P_i為平移的生成元（動量算符），C_i為伽利略變換的生成元，而L_ij為旋轉的生成元（角動量算符）。

現在我們可以對H'、P'_i、C'_i、L'_ij（反對稱張量）、M所張成的李群進行中心擴張，使得M與一切都可交換（位於中心，「中心擴張」因此得名）：

${\displaystyle [H',P'_{i}]=0\,\!}$

${\displaystyle [P'_{i},P'_{j}]=0\,\!}$

${\displaystyle [L'_{ij},H']=0\,\!}$

${\displaystyle [C'_{i},C'_{j}]=0\,\!}$

${\displaystyle [L'_{ij},L'_{kl}]=i[\delta _{ik}L'_{jl}-\delta _{il}L'_{jk}-\delta _{jk}L'_{il}+\delta _{jl}L'_{ik}]\,\!}$

${\displaystyle [L'_{ij},P'_{k}]=i[\delta _{ik}P'_{j}-\delta _{jk}P'_{i}]\,\!}$

${\displaystyle [L'_{ij},C'_{k}]=i[\delta _{ik}C'_{j}-\delta _{jk}C'_{i}]\,\!}$

${\displaystyle [C'_{i},H']=iP'_{i}\,\!}$

${\displaystyle [C'_{i},P'_{j}]=iM\delta _{ij}\,\!}$

參見

• 洛倫茲群
• 龐加萊群