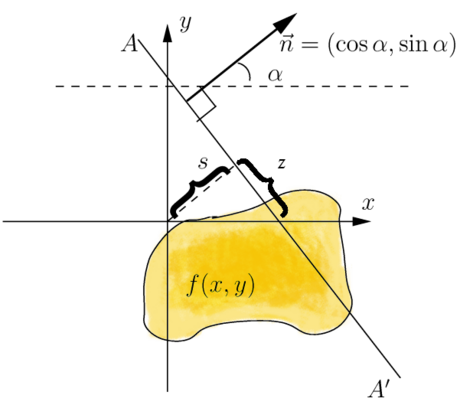
令密度函數 是一個的定義域為
是一個的定義域為  的緊支撐。令
的緊支撐。令 為拉東變換的運算子(operator),則
為拉東變換的運算子(operator),則 是一個定義在
是一個定義在
 空間中的直線
空間中的直線 ,它的定義如下
,它的定義如下

可以把直線  改寫成一個弧長
改寫成一個弧長 的參數式
的參數式

 是直線
是直線 和原點的距離,而
和原點的距離,而 是垂直於
是垂直於 的法線和
的法線和 軸的夾角,
接下來,我們可以令
軸的夾角,
接下來,我們可以令 當作
當作 平面上的新座標系統,把這個座標變換帶入到拉東變換得到
平面上的新座標系統,把這個座標變換帶入到拉東變換得到

更進一步,我們可以把 推廣到
推廣到 的歐幾里得空間,對一個緊支撐的連續函數
的歐幾里得空間,對一個緊支撐的連續函數 做拉東變換後的函數
做拉東變換後的函數 是定義在
是定義在
 的超平面上,
的超平面上,

積分的對象是自然超平面測度(natural hypersurface measure),而 是原本的
是原本的 的高維推廣。可以觀察到對
的高維推廣。可以觀察到對 裏的任意元素,
都是某個軌跡方程式的解
裏的任意元素,
都是某個軌跡方程式的解

而 是一個單位向量且屬於
是一個單位向量且屬於 ,
, ,n維的拉東變換可以改寫成定義在
,n維的拉東變換可以改寫成定義在  上的函數
上的函數

也可以藉由其他方式將拉東變換推廣,也就是對 的k維仿射子空間作(k-dimensional affine subspaces)積分。
而這種推廣拉東變換的特殊情況被廣泛應用在X射線電腦斷層掃描,他的做法是對一條直線積分。
的k維仿射子空間作(k-dimensional affine subspaces)積分。
而這種推廣拉東變換的特殊情況被廣泛應用在X射線電腦斷層掃描,他的做法是對一條直線積分。
拉東變換和傅立葉變換之間有很強的關聯性。單變量的傅立葉變換的定義是

而雙變量 的傅立葉變換是
的傅立葉變換是

把拉東變換的運算子的表記從}](//wikimedia.org/api/rest_v1/media/math/render/svg/15f797153d26de6695006b53c3d5b374b62fe439) 改成
改成 }](//wikimedia.org/api/rest_v1/media/math/render/svg/ca05f39a823774598e430ff88eecc89ddd009da8) 。根據投影切片定理學說,
。根據投影切片定理學說,
![{\displaystyle {\widehat {{\mathcal {R}}_{\alpha }[f]}}(\sigma )={\hat {f}}(\sigma \mathbf {n} (\alpha )),\quad \mathbf {n} (\alpha )=(\cos \alpha ,\sin \alpha )}](//wikimedia.org/api/rest_v1/media/math/render/svg/7b9b849ebddfdeaee53ee59098490ed5a830ea08)
因此一個初始函數沿着一條線傾角 的二維的傅立葉變換,相當於對拉東變換做一維的傅立葉變換。這個結果可以推廣到n維
的二維的傅立葉變換,相當於對拉東變換做一維的傅立葉變換。這個結果可以推廣到n維

對偶拉東變換是拉東變換的埃爾米特伴隨。令在空間 上的函數
上的函數 ,而對偶拉東變換的運算子定義為
,而對偶拉東變換的運算子定義為 。作用在
。作用在 上
上

積分的範圍是所有和 相交的超平面集合,而測度(measure)
相交的超平面集合,而測度(measure) 是集合
是集合 特殊的概率測度(Probability measure),
當對着
特殊的概率測度(Probability measure),
當對着 旋轉時,
旋轉時, 的值不會改變
的值不會改變
對於一個二維的拉東變換,其對偶變換是

在影像處理的文章中,對偶變換經常被稱作反向投影(back-projection) [2],因為它將平面中每條線上定義的函數 投影到該線上,從而生成圖像。
交結性質
根據拉普拉斯算子 在
在  的定義是
的定義是

這是一個旋轉不變性的二階微分算子,在空間 ,半徑的二階導數
,半徑的二階導數

也是旋轉不變性。
而拉東變換與其對偶變換屬於交結運算子(intertwining operator),是因為

重建處理是指從投影影像重建一個影像,或是一個函數 。重建處理是一種逆問題(inverse problem)。
。重建處理是一種逆問題(inverse problem)。
拉東反變換公式
對於二維拉東變換,最常被使用的解析公式(analytical formula) ,是Filtered Backprojection Formula或拉東反變換公式,反變換公式為
,是Filtered Backprojection Formula或拉東反變換公式,反變換公式為
 [3]
[3]
函數 滿足
滿足 [4],卷積核 (convolution kernel)
[4],卷積核 (convolution kernel)  在一些文章中稱作Ramp filter。
在一些文章中稱作Ramp filter。
不適定問題 (ill-posedness)
直覺上,反變換公式應該和微分類似, 。我們可以看的出來反變換公式
的行為類似微分。大致上來說,這個反變換公式把目標奇異化(singular);要如何量化拉東反轉化的不適定問題 (ill-posedness)呢?首先可以寫出
。我們可以看的出來反變換公式
的行為類似微分。大致上來說,這個反變換公式把目標奇異化(singular);要如何量化拉東反轉化的不適定問題 (ill-posedness)呢?首先可以寫出

 即是前面定義的反變換運算子,且伴隨着(adjoint to)拉東變換,因此
即是前面定義的反變換運算子,且伴隨着(adjoint to)拉東變換,因此 ,上式變成
,上式變成

複數指數函數 ,是
,是 的固有函數 (eigenfunction) ,
而特徵值 (eigenvalue)為
的固有函數 (eigenfunction) ,
而特徵值 (eigenvalue)為 。
。 的奇異值 (singular values) 是
的奇異值 (singular values) 是 ,
因為這些奇異值 (singular values)會趨近於0,所以
,
因為這些奇異值 (singular values)會趨近於0,所以 是無界的(unbounded) [4]。
是無界的(unbounded) [4]。
外顯(explicit)且計算效率好的拉東反變換公式,以及他的對偶是存在的。n維的反拉東變換可以由[5]

其中

而 是拉普拉斯算子(Laplacian),
是拉普拉斯算子(Laplacian), 是偽微分算子(pseudodifferential operator)
是偽微分算子(pseudodifferential operator)
=|2\pi \xi |^{n-1}{\mathcal {F}}\phi (\xi ).}](//wikimedia.org/api/rest_v1/media/math/render/svg/f74cd4b6777a1b180a2753a4e0267ba3f835854c)
 是傅立葉變換的運算子(operator)。
是傅立葉變換的運算子(operator)。
存档副本. [2017-06-29]. (原始內容存檔於2017-07-19). Kak, Avinash C.; Slaney, Malcolm. Principles of Computerized Tomographic Imaging. Classics in applied mathematics. Philadelphia: Society for Industrial and Applied Mathematics. 2001. ISBN 978-0-89871-494-4. 存档副本 (PDF). [2017-06-29]. (原始內容 (PDF)存檔於2018-11-25). 存档副本 (PDF). [2017-06-29]. (原始內容 (PDF)存檔於2018-11-25).
- Deans, Stanley R., The Radon Transform and Some of Its Applications, New York: John Wiley & Sons, 1983.
- Helgason, Sigurdur, Geometric analysis on symmetric spaces, Mathematical Surveys and Monographs 39 2nd, Providence, R.I.: American Mathematical Society, 2008, ISBN 978-0-8218-4530-1, MR 2463854.
- Helgason, Sigurdur, Groups and Geometric Analysis: Integral Geometry, Invariant Differential Operators, and Spherical Functions, Academic Press, 1984, ISBN 0-12-338301-3.
- Herman, Gabor T., Fundamentals of Computerized Tomography: Image Reconstruction from Projections 2nd, Springer, 2009, ISBN 978-1-85233-617-2.
- Minlos, R.A., Radon transform, Hazewinkel, Michiel (編), 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4.
- Natterer, Frank, The Mathematics of Computerized Tomography, Classics in Applied Mathematics 32, Society for Industrial and Applied Mathematics, ISBN 0-89871-493-1
- Natterer, Frank; Wübbeling, Frank, Mathematical Methods in Image Reconstruction, Society for Industrial and Applied Mathematics, ISBN 0-89871-472-9.
- Radon, Johann, Über die Bestimmung von Funktionen durch ihre Integralwerte längs gewisser Mannigfaltigkeiten, Berichte über die Verhandlungen der Königlich-Sächsischen Akademie der Wissenschaften zu Leipzig, Mathematisch-Physische Klasse [Reports on the proceedings of the Royal Saxonian Academy of Sciences at Leipzig, mathematical and physical section] (Leipzig: Teubner), 1917, (69): 262–277; Translation: Radon, J.; Parks, P.C. (translator), On the determination of functions from their integral values along certain manifolds, IEEE Transactions on Medical Imaging, 1986, 5 (4): 170–176, PMID 18244009, doi:10.1109/TMI.1986.4307775.
- Roerdink, J.B.T.M., Tomography, Hazewinkel, Michiel (編), 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4.
- 埃里克·韋斯坦因. 拉東變換. MathWorld..

































}](http://wikimedia.org/api/rest_v1/media/math/render/svg/15f797153d26de6695006b53c3d5b374b62fe439)
}](http://wikimedia.org/api/rest_v1/media/math/render/svg/ca05f39a823774598e430ff88eecc89ddd009da8)
![{\displaystyle {\widehat {{\mathcal {R}}_{\alpha }[f]}}(\sigma )={\hat {f}}(\sigma \mathbf {n} (\alpha )),\quad \mathbf {n} (\alpha )=(\cos \alpha ,\sin \alpha )}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7b9b849ebddfdeaee53ee59098490ed5a830ea08)



























=|2\pi \xi |^{n-1}{\mathcal {F}}\phi (\xi ).}](http://wikimedia.org/api/rest_v1/media/math/render/svg/f74cd4b6777a1b180a2753a4e0267ba3f835854c)