德拉瓦噴嘴

德拉瓦噴嘴（de Laval nozzle, 亦稱漸縮漸闊噴嘴，convergent-divergent nozzle、CD nozzle或con-di nozzle）是一個中間收縮、不對稱沙漏狀的管子。藉由將流體的熱能轉化為動能，可將通過它的熱壓縮氣體加速到超音速。氣體在截面積最小處恰好達到音速。 被廣泛用作蒸汽渦輪機及火箭發動機噴嘴，亦可見於超音速噴射發動機。 類似的流動性質已經應用於天體物理學中的噴射流。

德拉瓦噴嘴 速度由左至右增加

德拉瓦噴嘴示意圖，顯示流體速度(V)、溫度(T)及壓力(P)在通過德拉瓦噴嘴時的變化

歷史

西元1888年，由瑞典發明家Gustaf de Laval開發，並使用在蒸汽渦輪機上。

最早被羅伯特·戈達德用作火箭發動機，大多數使用高溫燃燒氣體的現代火箭發動機都使用德拉瓦噴嘴。

運作

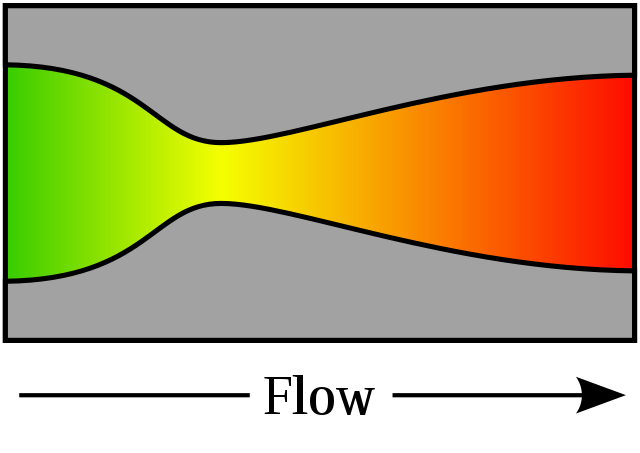
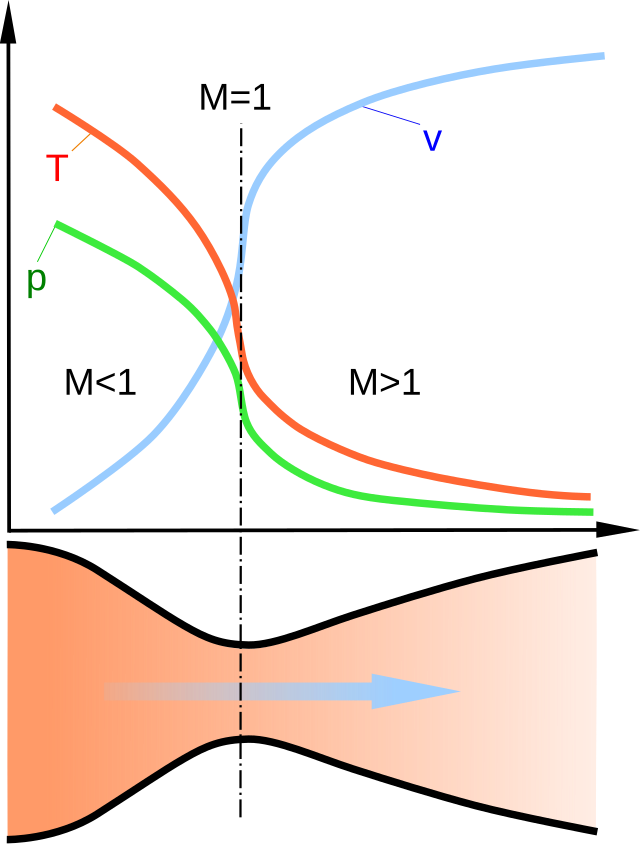
其操作有賴於亞音速和超音速氣體的不同特性。 如果由於質量流量不變而管道變窄，則亞音速氣體流速將會增加。 通過德拉瓦噴嘴的氣流是等熵的（氣體熵幾乎不變）。在亞音速流中，氣體是可壓縮的，聲音會通過它傳播。 在橫截面面積最小的喉部，氣體速度局部達到聲速（馬赫數= 1.0），這種狀況稱為阻流。 隨着噴嘴橫截面積的增加，氣體開始膨脹，氣流加速到超音速，在那裏聲波不會通過氣體向後傳播（馬赫數> 1.0）。

運作情況

只有在通過噴嘴的壓力和質量流量足以達到音速的狀況下，德拉瓦噴嘴會在喉部產生阻流現象。若是沒有達到條件，則不會有超音速氣流產生，此時運作方式較接近文氏管。這要求噴嘴的入口壓力始終顯著高於環境壓力（亦即噴流的靜止壓力必須高於環境壓力）。

另外，噴嘴出口處的氣體壓力不能太低。出口壓力雖然可以低於其排出的環境壓力，但是如果低得太超過，那麼氣流將不再為超音速，或者將在噴嘴的擴張部剝離，形成噴嘴內的紊流，產生側向推力並可能損壞噴嘴。

實務上，出口處超音速氣流壓力必須高於約2-3倍環境壓力，氣體才能離開噴嘴。

氣流狀態分析

通過德拉瓦噴嘴的氣流分析涉及許多概念和假設：

• 為簡單起見，氣體被認為是理想的氣體
• 氣體流動是等熵過程。在此假設下，流動是可逆的（無摩擦及消耗），並且絕熱（即沒有獲得或失去熱量）
• 在推進劑燃燒期間氣流穩定且恆定
• 氣流方向沿着一條從氣體入口到廢氣出口的直線（即，沿着噴嘴的對稱軸線）
• 氣流行為是可壓縮的，因為有着極高的流速（馬赫數> 0.3）

排氣速度

氣體以亞音速進入噴嘴，隨着噴管收縮，氣體被迫加速，直到截面積最小的噴嘴喉部時，恰好達到音速。擴張部從喉部開始，截面積逐漸加大，氣體跟着膨脹，漸漸超越音速。 可用以下等式來計算排出氣體的線速度：

${\displaystyle v_{e}={\sqrt {{\frac {TR}{M}}\cdot {\frac {2\gamma }{\gamma -1}}\cdot \left[1-\left({\frac {p_{e}}{p}}\right)^{\frac {\gamma -1}{\gamma }}\right]}},}$

代號解釋:
${\displaystyle v_{e}}$	= 噴嘴出口處的排氣速度
${\displaystyle T}$	= 輸入氣體的絕對溫度
${\displaystyle R}$	= 理想氣體常數
${\displaystyle M}$	= 氣體莫耳質量
${\displaystyle \gamma }$	= ${\displaystyle {\frac {c_{p}}{c_{v}}}}$ = 等熵擴張因子
	(${\displaystyle c_{p}}$ and ${\displaystyle c_{v}}$ 分別是定壓和定容的氣體的比熱),
${\displaystyle p_{e}}$	= 噴嘴出口處氣體的絕對壓力
${\displaystyle p}$	= 輸入氣體的絕對壓力

一些典型火箭發動機推進劑的排氣速度${\displaystyle v_{e}}$值如下：

• 單組元液體推進劑1,700～2,900m / s（3,800～6,500mph）
• 雙組元液體推進劑2,900～4,500m / s（6,500～10,100mph）
• 固體推進劑2,100～3,200m / s（4,700～7,200mph）

值得注意的一點是，基於排出氣體表現為理想氣體的假設，${\displaystyle v_{e}}$有時也被稱作理想排氣速度。

使用上述等式的舉例如下： 假定推進劑燃燒後排出氣體：進入噴嘴的絕對壓力${\displaystyle p}$ = 7.0MPa，並在絕對壓力${\displaystyle p_{e}}$ = 0.1MPa下離開火箭排氣口。在絕對溫度${\displaystyle T}$ = 3500K下，具有等熵膨脹因子γ= 1.22和莫耳質量${\displaystyle M}$ = 22kg / kmol。 使用上述公式計算可得出排氣速度${\displaystyle v_{e}}$ = 2802 m / s（2.80 km / s），這與上述典型值一致。

在閱讀技術文獻時可能感到困惑，因為許多作者並沒有解釋他們是使用理想氣體常數${\displaystyle R}$，或者他們使用氣體定律常數${\displaystyle R_{s}}$，這只適用於特定氣體。 兩個常數之間的關係是${\displaystyle R_{s}}$ = ${\displaystyle R}$ / ${\displaystyle M}$。

推導

音速是一個與密度有關的量。流體速度與音速的比值被稱為馬赫數：

${\displaystyle M={\frac {c}{a}}}$ …… (1)

由歐拉方程和理想氣體狀態方程式可得出：

${\displaystyle dp/d\rho =a^{2}}$:

${\displaystyle c{\frac {dc}{dx}}=-{\frac {1}{\rho }}{\frac {dp}{dx}}=-{\frac {1}{\rho }}{\frac {dp}{d\rho }}{\frac {d\rho }{dx}}=-{\frac {a^{2}}{\rho }}{\frac {d\rho }{dx}}}$,

${\displaystyle {\frac {1}{\rho }}{\frac {d\rho }{dx}}=-M^{2}{\frac {1}{c}}{\frac {dc}{dx}}}$……(2),

方程（2）表明，沿着流線方向，氣體密度變化和速度變化是成正比的，係數為${\displaystyle M^{2}}$。由此可得，亞音速狀態下，密度變化小於速度變化；相反，超音速狀態下，密度變化大於速度變化。

然後根據連續性假設，

${\displaystyle \rho cA={\mathsf {const}}}$,

${\displaystyle \ln \rho +\ln c+\ln A=\ln({\mathsf {const}})}$,

${\displaystyle {\frac {d\rho }{\rho }}+{\frac {dc}{c}}+{\frac {dA}{A}}=0}$.

沿流線求導，有

${\displaystyle {\frac {1}{c}}{\frac {dc}{dx}}={\frac {1}{M^{2}-1}}{\frac {1}{A}}{\frac {dA}{dx}}}$……(3).

如果把截面積A(x)當作已知，流速c(x)，馬赫數M(x)當作未知，由方程（3）就可對流動狀況進行討論。如果相對流體進行加速，則必須dc/dx > 0，由(3)

• 可得亞音速流動(M < 1),從而dA/dx < 0，管路變窄。對超音速流動(M > 1), dA/dx > 0，管路變寬。
• 對於音速流動，管路截面積不變。

參考資料

相關條目