音分

音分（英語：cent）是度量音程的對數標度單位，在十二平均律中，將一個八度音程分為12個半音。每一個半音的音程（相當於相鄰鋼琴鍵間的音程）等於100音分。音分通常用於度量極小的音程，或是用於對比不同調律系統中可比音程的大小差異。然而若是兩個相鄰音符間的音程只有相差1音分時，由於差距極為微小，人耳很難辨別。

1830年代，在羅伯特·霍爾福德·麥克道威爾·鮑桑葵（Robert Holford Macdowell Bosanquet）的建議下，音響學者、比較音樂學者亞歷山大·約翰·埃利斯（Alexander John Ellis）以加斯帕德·戴普羅尼（Gaspard de Prony）發展的「聲學對數」（acoustic logarithms）十進制半音系統度量法為基礎，將音分的概念引入他翻譯的赫爾曼·馮·亥姆霍茲著作《音調的感覺》（On the Sensations of Tone）。音分已經成為表示和對比音高及音程的相對標準的方法。

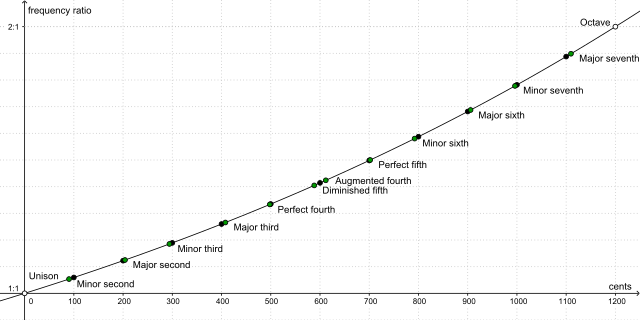
1200音分等於一個八度音程，頻率比為2:1，等程半音（相當於相鄰鋼琴鍵間的音程）等於100音分，代表1音分正好等於2^1/1200，即 ${\sqrt[{1200}]{2}}$ ，近似1.0005777895。

如果知道兩個音a和b的頻率，兩個音相距的音分值n可用下列公式計算（類似分貝定義式的形式，目的是為了使指數形式的物理單位線性化，使其化為對數）：

n=1200\log _{2}\left({\frac {a}{b}}\right)\approx 3986\log _{10}\left({\frac {a}{b}}\right)

同樣地，如果知道音b和音分值n，那麼另一個音a可用下列公式算出：

a=b\times 2^{\frac {n}{1200}}

為了比較不同的調律系統，會把不同的音程差距用音分表示。例如在純律中，大三度用頻率比表示為5:4，使用上面的公式可算出其約為386音分，在十二平均律鋼琴的等分音程中則為400音分。這14音分的差距，大約是一個半度的1/7，是很容易聽出來的。人類的最小可覺差大約是6音分，某些聽力較好的人可以達到4~5音分。

人類可察覺的音分差是難以確定的，每個人的分辨能力都是不同的。一位作家曾說過人類能分辨5－6音分的音高差距。^[2] 分辨音分差的閾限也會因為音高的音色作用而明顯變化。在一項研究中，音色的變化降低了學生音樂家識別走調音的能力，使他們識別音高的誤差達到了±12音分。^[3] 這項研究中也確認，如果聽者能更明白的知道音高的前後關係，他們對音高的判斷會更準確。^[4]

當人在聽樂器的顫音時，有證據表明人類能感知到的是如中心音高一樣的平均頻率。^[5] 一項關於西方聲樂顫音的研究發現顫音的音分變化範圍都會在±34音分和±123間，平均變化±71音分，在威爾第歌劇的詠嘆調中顫音的變化更大。^[6]

普通成人可以清楚分辨至少25音分的音高差，而患有失樂感症的成人不能分辨小於100音分的音程差，有時分辨更大的音程差都是有困難的。^[7]

下列音頻文件播放的第一個音都是中音C，下一個音均比其更尖銳。