貝氏網路

貝氏網路（Bayesian network），又稱信念網絡（belief network）或是有向無環圖模型（directed acyclic graphical model），是一種機率圖型模型，藉由有向無環圖（directed acyclic graphs, or DAGs）中得知一組隨機變數${\displaystyle \left\{X_{1},X_{2},...,X_{n}\right\}}$及其n組條件機率分配（conditional probability distributions, or CPDs）的性質。舉例而言，貝氏網路可用來表示疾病和其相關症狀間的機率關係；倘若已知某種症狀下，貝氏網路就可用來計算各種可能罹患疾病之發生機率。

一個簡單的貝氏網路。雨水影響灑水器是否有動作，且雨水及灑水器二者均可影響草是否濕潤.

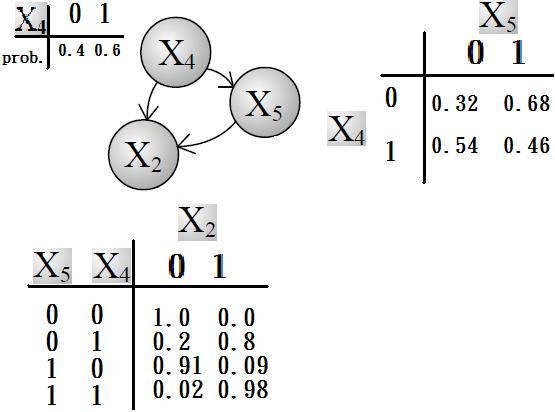
一般而言，貝氏網路的有向無環圖中的節點表示隨機變數，它們可以是可觀察到的變量，抑或是潛在變量、未知參數等。連接兩個節點的箭頭代表此兩個隨機變數是具有因果關係或是非條件獨立的；而兩個節點間若沒有箭頭相互連接一起的情況就稱其隨機變數彼此間為條件獨立。若兩個節點間以一個單箭頭連接在一起，表示其中一個節點是「因（parents）」，另一個是「果（descendants or children）」，兩節點就會產生一個條件機率值。比方說，我們以${\displaystyle X_{i}}$表示第i個節點，而${\displaystyle X_{i}}$的「因」以${\displaystyle P_{i}}$表示，${\displaystyle X_{i}}$的「果」以${\displaystyle C_{i}}$表示；圖一就是一種典型的貝氏網路結構圖，依照先前的定義，我們就可以輕易的從圖一可以得知：

${\displaystyle P_{2}=\left\{X_{4},X_{5}\right\},C_{2}=\emptyset ,P_{4}=\emptyset ,C_{4}=\left\{X_{2},X_{5}\right\},P_{5}=\left\{X_{4}\right\}}$，以及${\displaystyle C_{5}=\left\{X_{2}\right\}}$

大部分的情況下，貝氏網路適用在節點的性質是屬於離散型的情況下，且依照${\displaystyle P(X_{i}|P_{i})}$此條件機率寫出條件機率表（英語：conditional probability table），此條件機率表的每一列（row）列出所有可能發生的${\displaystyle P_{i}}$，每一行（column）列出所有可能發生的${\displaystyle X_{i}}$，且任一列的機率總和必為1。寫出條件機率表後就很容易將事情給條理化，且輕易地得知此貝氏網路結構圖中各節點間之因果關係；但是條件機率表也有其缺點：若是節點${\displaystyle X_{i}}$是由很多的「因」所造成的「果」，如此條件機率表就會變得在計算上既複雜又使用不便。下圖為圖一貝氏網路中某部分結構圖之條件機率表。

圖一：部分結構圖之條件機率表

數學定義

令 G = (I,E) 表示一個有向無環圖（DAG），其中 I 代表圖中所有的節點的集合，而 E 代表有向連接線段的集合，且令 X = (X_i)_i∈I 為其有向無環圖中的某一節點 i 所代表之隨機變數，若節點 X 的聯合機率分配可以表示成：

${\displaystyle p(x)=\prod _{i\in I}p{\big (}x_{i}\,{\big |}\,x_{\operatorname {pa} (i)}{\big )}}$

則稱 X 為相對於一有向無環圖 G 的貝氏網路，其中${\displaystyle pa(i)}$表示節點 i 之「因」。

對任意的隨機變數，其聯合分配可由各自的局部條件機率分配相乘而得出：

${\displaystyle \mathrm {P} (X_{1}=x_{1},\ldots ,X_{n}=x_{n})=\prod _{i=1}^{n}\mathrm {P} (X_{i}=x_{i}\mid X_{i+1}=x_{i+1},\ldots ,X_{n}=x_{n})}$

依照上式，我們可以將一貝氏網路的聯合機率分配寫成：

${\displaystyle \mathrm {P} (X_{1}=x_{1},\ldots ,X_{n}=x_{n})=\prod _{i=1}^{n}\mathrm {P} (X_{i}=x_{i}\mid X_{j}=x_{j})}$（對每個相對於X_i的「因」變數 X_j 而言)

上面兩個表示式之差別在於條件機率的部分，在貝氏網路中，若已知其「因」變數下，某些節點會與其「因」變數條件獨立，只有與「因」變數有關的節點才會有條件機率的存在。

如果聯合分配的相依數目很稀少時，使用貝氏函數的方法可以節省相當大的記憶體容量。舉例而言，若想將10個變數其值皆為0或1儲存成一條件機率表型式，一個直觀的想法可知我們總共必須要計算${\displaystyle 2^{10}=1024}$個值；但若這10個變數中無任何變數之相關「因」變數是超過三個以上的話，則貝氏網路的條件機率表最多只需計算${\displaystyle 10*2^{3}=80}$個值即可。另一個貝式網路優點在於：對人類而言，它更能輕易地得知各變數間是否條件獨立或相依與其局部分配（local distribution）的型態來求得所有隨機變數之聯合分配。

馬可夫毯（Markov blanket）

定義一個節點之馬可夫毯為此節點的因節點、果節點與果節點的因節點所成之集合。一旦給定其馬可夫毯的值後，若網路內之任一節點X皆會與其他的節點條件獨立的話，就稱X為相對於一有向無環圖G的貝氏網路。

舉例說明

假設有兩個伺服器${\displaystyle (S_{1},S_{2})}$，會傳送封包到使用者端（以U表示之），但是第二個伺服器的封包傳送成功率會與第一個伺服器傳送成功與否有關，因此此貝氏網路的結構圖可以表示成如圖二的型式。就每個封包傳送而言，只有兩種可能值：T（成功）或 F（失敗）。則此貝氏網路之聯合機率分配可以表示成：

${\displaystyle P(U,S_{1},S_{2})=P(U|S_{1},S_{2})\times P(S_{2}|S_{1})\times P(S_{1})}$

圖二：簡單的貝氏網路例子

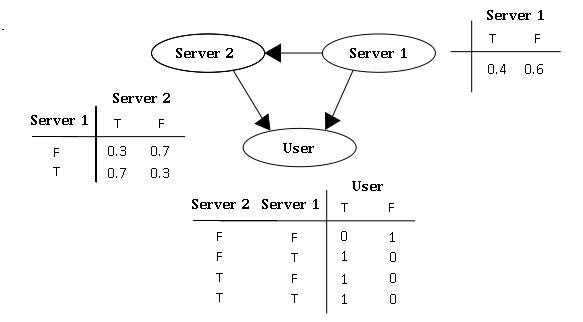
此模型亦可回答如：「假設已知使用者端成功接受到封包，求第一伺服器成功發送封包的機率?」諸如此類的問題，而此類型問題皆可用條件機率的方法來算出其所求之發生機率：

${\displaystyle \mathrm {P} ({\mathit {S_{1}}}=T\mid {\mathit {U}}=T)={\frac {\mathrm {P} ({\mathit {S_{1}}}=T,{\mathit {U}}=T)}{\mathrm {P} ({\mathit {U}}=T)}}}$

${\displaystyle ={\frac {\sum _{{\mathit {S_{2}}}\in \{T,F\}}\mathrm {P} ({\mathit {S_{1}}}=T,{\mathit {S_{2}}},{\mathit {U}}=T)}{\sum _{{\mathit {S_{1}}},{\mathit {S_{2}}}\in \{T,F\}}\mathrm {P} ({\mathit {U}}=T,{\mathit {S_{1}}},{\mathit {S_{2}}})}}}$

${\displaystyle ={\frac {(0.4\times 0.3\times 1)_{U=T,S_{1}=T,S_{2}=F}+(0.4\times 0.7\times 1)_{U=T,S_{1}=T,S_{2}=T}}{(0.4\times 0.3\times 1)_{TTF}+(0.4\times 0.7\times 1)_{TTT}+(0.6\times 0.3\times 1)_{FTT}+0_{TFF}}}}$

${\displaystyle \approx 68.96\%}$。

求解方法

以上例子是一個很簡單的貝氏網路模型，但是如果當模型很複雜時，這時使用列舉式的方法來求解機率就會變得非常複雜且難以計算，因此必須使用其他的替代方法。一般來說，貝氏機率有以下幾種求法：

精確推論

• 列舉推理法（如上述例子）
• 變數消元演算法（variable elimination）

隨機推論（蒙地卡羅方法）

• 直接取樣演算法
• 拒絕取樣演算法
• 概似加權演算法
• 馬可夫鏈蒙地卡羅演算法（Markov chain Monte Carlo algorithm）

在此，以馬可夫鏈蒙地卡羅演算法為例，又馬可夫鏈蒙地卡羅演算法的類型很多，故在這裡只說明其中一種吉布斯採樣的操作步驟： 首先將已給定數值的變數固定，然後將未給定數值的其他變數隨意給定一個初始值，接著進入以下迭代步驟：

（1）隨意挑選其中一個未給定數值的變數

（2）從條件分配${\displaystyle P(X_{i}|{\text{Markovblanket}}(X_{i}))}$抽樣出新的${\displaystyle X_{i}}$的值，接著重新計算${\displaystyle P(X_{i}|{\text{Markovblanket}}(X_{i}))=\alpha P(X_{i}|{\text{parents}}(X_{i}))\times \prod _{Y_{i}\in {\text{children}}(X_{i})}{\text{parent}}(Y_{i})}$

當迭代結束後，刪除前面若干筆尚未穩定的數值，就可以求出的近似條件機率分配。馬可夫鏈蒙地卡羅演算法的優點是在計算很大的網路時效率很好，但缺點是所抽取出的樣本並不具獨立性。

當貝氏網路上的結構跟參數皆已知時，我們可以透過以上方法來求得特定情況的機率，不過，如果當網路的結構或參數未知時，我們必須藉由所觀測到的資料去推估網路的結構或參數，一般而言，推估網路的結構會比推估節點上的參數來的困難。依照對貝氏網路結構的了解和觀測值的完整與否，我們可以分成下列四種情形：

結構	觀測值	方法
已知	完整	最大概似估計法（MLE）
已知	部份	EM演算法 Greedy Hill-climbing method
未知	完整	搜尋整個模型空間
未知	部份	結構演算法 EM演算法 Bound contraction

以下就結構已知的部分，作進一步的說明。

1.結構已知，觀測值完整：

此時我們可以用最大概似估計法（MLE）來求得參數。其對數概似函數為

${\displaystyle L={\frac {1}{N}}\sum _{i=1}^{n}\sum _{i=1}^{s}\log(P(X_{i}|pa(X_{i}),D_{i}))}$

其中${\displaystyle pa(X_{i})}$代表${\displaystyle X_{i}}$的因變數，${\displaystyle D_{i}}$代表第${\displaystyle {\mathit {1}}}$個觀測值，N代表觀測值資料的總數。

以圖二當例子，我們可以求出節點U的最大概似估計式為

${\displaystyle P(U=u|S_{1}=s_{1},S_{2}=s_{2})={\frac {n(U=u,S_{1}=s_{1},S_{2}=s_{2})}{n(S_{1}=s_{1},S_{2}=s_{2})}}}$

由上式就可以藉由觀測值來估計出節點U的條件分配。如果當模型很複雜時，這時可能就要利用數值分析或其它最佳化技巧來求出參數。

2.結構已知，觀測值不完整（有遺漏資料）：

如果有些節點觀測不到的話，可以使用EM演算法（Expectation-Maximization algorithm）來決定出參數的區域最佳概似估計式。而EM演算法的主要精神在於如果所有節點的值都已知下，在M階段就會很簡單，如同最大概似估計法。而EM演算法的步驟如下：

（1）首先給定欲估計的參數一個起始值，然後利用此起始值和其他的觀測值，求出其他未觀測到節點的條件期望值，接著將所估計出的值視為觀測值，將此完整的觀測值帶入此模型的最大概似估計式中，如下所示（以圖二為例）：

${\displaystyle P(U=u|S_{1}=s_{1},S_{2}=s_{2})={\frac {EN(U=u,S_{1}=s_{1},S_{2}=s_{2})}{EN(S_{1}=s_{1},S_{2}=s_{2})}}}$

其中${\displaystyle EN(x)}$代表在目前的估計參數下，事件x的條件機率期望值為

${\displaystyle EN(x)=E\sum _{k}I(x|D(k))=\sum _{k}P(x|D(k))}$

（2）最大化此最大概似估計式，求出此參數之最有可能值，如此重複步驟（1）與（2），直到參數收斂為止，即可得到最佳的參數估計值。

補充例子（列舉推理法）

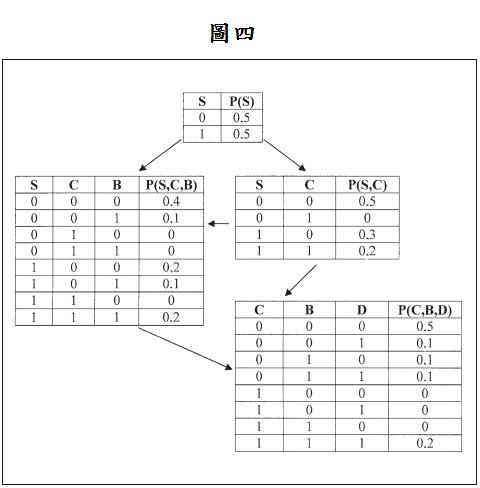
讓我們考慮一個應用在醫藥上的機率推論例子，在此病人會被診斷出是否有呼吸困難的症狀。表一代表一個我們所觀測到的資料集合，包含10筆觀測值，S代表的是吸菸與否（Smoker），C代表是否為罹癌者（Cancer），B代表是否罹患支氣管炎（bronchitis），D代表是否有呼吸困難及咳嗽（dyspnea and asthma）的症狀。『1』和『0』分別代表『是』和『否』。此醫藥網路結構顯示於圖三。

表一

表二代表的是整個網路的經驗聯合機率分配，是由所收集到的資料所建構而成，利用此表可建構出節點的聯合機率分配。見圖四。此貝氏公式${\displaystyle P(A|B)={\frac {P(A,B)}{P(B)}}}$可利用節點的邊際機率和聯合機率去計算節點的條件機率，待會會應用在建立條件機率表格（Conditional probability Table; CPT）上。見圖五。貝氏網路的聯合機率可由下列式子計算：

${\displaystyle P(S,C,B,D)=P(S)\times P(C|S)\times P(B|S,C)\times P(D|B,C)}$

其值見表三。

使用整個網路經驗聯合機率分配所計算出來的值會與使用CPT所計算出來的值不同，其差異可由表二和表三得知。其中差異不只是值的不同，也出現了新事件的機率（原本所沒觀察到的事件）。

表二

圖四

圖五

表三

建立在觀測資料上的機率推論演算法：

1.資料集合${\displaystyle D=\left\{d_{1},\ldots ,d_{n}\right\}}$，其中${\displaystyle d_{i}={x_{i}^{(1)},\ldots ,x_{i}^{(N)}}}$（下標代表第幾個觀測值，上標代表第幾個變數），且一共有n個觀測值。每一個觀測值包含${\displaystyle N(N\geq 2)}$個變數${\displaystyle {X_{i}^{(1)},\ldots ,X_{i}^{(N)}}}$，第j個變數有${\displaystyle A^{(j)}={0,1,\ldots ,\alpha ^{(j)}-1}(\alpha ^{(j)}\geq 2)}$狀態。

2.此貝氏網路的結構G代表N個前代（predecessors）節點集合${\displaystyle \left\{\Pi ^{(1)},\ldots ,\Pi ^{(N)}\right\}}$，也就是對第j個節點，${\displaystyle \Pi ^{(j)}}$為其親代節點的集合, j=1,2,…,N

3.範例點（instantiated node）${\displaystyle \left\{X^{P_{1}}=x^{P_{1}},\ldots ,X^{P_{v}}=x^{P_{v}}\right\}}$為節點在已知狀態，即在此狀態的機率為1。如果範例點為空集合，將使用古典機率推論

使用表一的觀測值和圖一的貝氏網路結構，並且已知範例點（instantiated node）為${\displaystyle \left\{S=0,C=0\right\}}$，也就是病人為非吸菸者和罹癌者：${\displaystyle P\left(S=0\right)=1,P\left(C=0\right)=1}$

問題：
1.病人患有支氣管炎的機率${\displaystyle P\left(B\right)=?}$
2.病人會有呼吸困難的機率${\displaystyle P\left(D\right)=?}$

解答：
1. ${\displaystyle P\left(B=0|S=0,C=0\right)=0.8}$

${\displaystyle P\left(B=1|S=0,C=0\right)=0.2}$
故為0.2

2. ${\displaystyle P\left(D=0|S=0,C=0\right)}$

${\displaystyle =P\left(D=0,B=0|S=0,C=0\right)+P\left(D=0,B=1|S=0,C=0\right)}$

${\displaystyle =P\left(D=0|B=0,S=0,C=0\right)\times P\left(B=0|S=0,C=0\right)}$

${\displaystyle +P\left(D=0|B=1,S=0,C=0\right)\times P\left(B=1|S=0,C=0\right)}$

${\displaystyle P\left(D=1|S=0,C=0\right)}$

${\displaystyle =P\left(D=1,B=1|S=0,C=0\right)+P\left(D=1,B=0|S=0,C=0\right)}$

${\displaystyle =P\left(D=1|B=0,S=0,C=0\right)\times P\left(B=0|S=0,C=0\right)}$

${\displaystyle +P\left(D=1|B=1,S=0,C=0\right)\times P\left(B=1|S=0,C=0\right)}$

應用

貝氏網路目前應用在類比計算生物學與生物資訊學基因調控網路（英語：gene regulatory networks）、蛋白質結構、基因表達分析、醫學、文檔分類、資訊檢索、決策支援系統、工程學、資料結合（英語：data fusion）、圖像處理等。

參考文獻

• A. N. Terent' yev and P. I. Bidyuk. METHOD OF PROBABILISTIC INFERENCE FROM LEARNING DATA IN BAYESIAN NETWORKS. Cybernetics and Systems Analysis, 391-396, Vol. 43, No. 3, 2007
• Emilia Mendes and Nile Mosley. Bayesian Network Models for Web Effort Prediction: A Comparative Study. IEEE TRANSACTIONS ON SOFTWARE ENGINEERING, 723-737, VOL. 34, NO. 6, NOVEMBER/DECEMBER 2008
• Yu. V. Kapitonova, N. M. Mishchenko, O. D. Felizhanko, and N. N. Shchegoleva. USING BAYESIAN NETWORKS FOR MONITORING COMPUTER USERS. Cybernetics and Systems Analysis, 789-799, Vol. 40, No. 6, 2004
• Ben-Gal I., Bayesian Networks, in Ruggeri F., Faltin F. & Kenett R. ,Encyclopedia of Statistics in Quality & Reliability, Wiley & Sons (2007).
• Radu Stefan Niculescu, Tom M. Mitchell and R. Bharat Rao, Journal of Machine Learning Research 7 (2006) 1357–1383
• N. Terent' yev and P. I. Bidyuk. METHOD OF PROBABILISTIC INFERENCE FROM LEARNING DATA IN BAYESIAN NETWORKS. Cybernetics and Systems Analysis, 391-396, Vol. 43, No. 3, 2007
• P. I. Bidyuk, A. N. Terent』ev, and A. S. Gasanov. CONSTRUCTION AND METHODS OF LEARNING OF BAYESIAN NETWORKS. Cybernetics and Systems Analysis, 587-598, Vol. 41, No. 4, 2005

外部連結

• A tutorial on learning with Bayesian Networks
• An Introduction to Bayesian Networks and their Contemporary Applications （頁面存檔備份，存於網際網路檔案館）
• On-line Tutorial on Bayesian nets and probability （頁面存檔備份，存於網際網路檔案館）
• Web-App to create Bayesian nets and run it with a Monte Carlo method
• Continuous Time Bayesian Networks （頁面存檔備份，存於網際網路檔案館）
• Bayesian Networks: Explanation and Analogy
• A live tutorial on learning Bayesian networks （頁面存檔備份，存於網際網路檔案館）
• A hierarchical Bayes Model for handling sample heterogeneity in classification problems （頁面存檔備份，存於網際網路檔案館）, provides a classification model taking into consideration the uncertainty associated with measuring replicate samples.
• Hierarchical Naive Bayes Model for handling sample uncertainty （頁面存檔備份，存於網際網路檔案館）, shows how to perform classification and learning with continuous and discrete variables with replicated measurements.