幾何變換

幾何變換（geometric transformation）是指從具有幾何結構之集合至其自身或其他此類集合的一種對射。具體來說，「幾何變換是一個函數，其定義域與值域為點集合。幾何變換最常見的定義域與值域為同時為R²，或同時為R³。其他的幾何變換則要求須為一對一函數，使之有反函數^[1]。」可透過研究這些變換的方法來研究幾何^[2]。

幾何變換可以其操作集合的維度來分類（因此可分類出平面變換與空間變換等）。幾何變換亦可依據其保留其性質來分類：

• 位移保留距離與方向角度；
• 等距同構保留距離與角度^[3]；
• 相似保留距離間的比例；
• 仿射變換保留平行^[3]；
• 投影變換保留共線性^[4]；

以上每種變換均包含前一種變換^[4]。

• 反演在平面上保留所有線及圓所組成的集合（但可能替換線與圓），而莫比烏斯變換則保留三維空間內的所有平面與球。

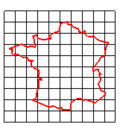
以法國地圖為例：

• 
  原圖案
• 
  等距同構
• 
  相似
• 
  仿射變換
• 
  投影變換
• 
  反演

• 微分同胚為一階仿射的變換；前面所有變換都是微分同胚的特例^[5]。

• 共形變換保留角度在一階的相似。

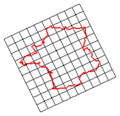
• 保積變換保留在平面上的面積，或在三維空間上的容量^[6]。該變換為行列式為1的一階仿射變換。

• 同胚保留點的鄰域。

• 
  共形變換
• 
  保積變換
• 
  微分同胚
• 
  同胚

相同類型的群變換可能是其他變換群的子群。

另見

• 愛爾蘭根綱領
• 拓撲學
• 剛性變換