三側錐三角柱

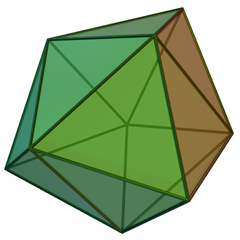
三側錐三角柱（Triaugmented triangular prism）又稱四角化三角柱（Tetrakis triangular prism）^[1]:41，由14個正三角形組成，由於這種多面體的面都是三角形，因此是一種十四面的三角面多面體^[2]，其亦屬於詹森多面體之一，索引為J₅₁^[2]。形如其名地，它可由三個正四角錐（J₁）以底面黏合在一個正三角柱的側面上組合而成，這與側錐三角柱（J₄₉）和二側錐三角柱（J₅₀）有著極為相似的構造。詹森多面體是凸多面體，面皆由正多邊形組成但不屬於均勻多面體，共有92種。這些立體最早在1966年由諾曼·詹森（英語：Norman Johnson (mathematician)）（Norman Johnson）命名並給予描述^[3]。

三側錐三角柱

類別	詹森多面體 J50 - J51 - J52
對偶多面體	結合多面體（英語：Associahedron） K5
識別
名稱	三側錐三角柱
參考索引	J51
鮑爾斯縮寫 （verse-and-dimensions的wikia：Bowers acronym）	tautip
數學表示法
康威表示法	k4P3
性質
面	14
邊	21
頂點	9
歐拉特徵數	F=14, E=21, V=9 （χ=2）
組成與佈局
面的種類	14個三角形
頂點圖	3個(34) 6個(35)
對稱性
對稱群	D3h群
特性
凸多面體、 三角形多面體
圖像
結合多面體（英語：Associahedron） K5 （對偶多面體） （展開圖）
閱 論 編

性質

三側錐三角柱共由14個面、21條邊和9個頂點組成^[4][5][6]。組成三側錐三角柱的14個面都是正三角形。在其9個頂點中，有3個頂點是4個三角形的公共頂點^[6]，在頂點圖中可以用[3⁴]來表示^[7]、另外6個頂點是5個三角形的公共頂點^[6]，在頂點圖中可以用[3⁵]來表示^[7]。

體積與表面積

若一個三側錐三角柱邊長為${\displaystyle a}$，則其體積${\displaystyle V}$與表面積${\displaystyle A}$為：^[8][2]

${\displaystyle V={\frac {2{\sqrt {2}}+{\sqrt {3}}}{4}}a^{3}\approx 1.14012a^{3}}$

${\displaystyle A={\frac {7{\sqrt {3}}}{2}}a^{2}\approx 6.06218a^{2}}$

二面角

三側錐三角柱有3種二面角，這三種二面角皆為三角形和三角形的二面角，但位置不同，其角度分別為：

位於兩個相異側錐側面的交角角度為：^[7]

${\displaystyle \arccos \left(-{\frac {1+2{\sqrt {6}}}{6}}\right)\approx 2.957830\approx 169.471221^{\circ }}$

位於底面和側錐側面的交角角度為負根號三分之二的反餘弦值，約為144.7356度：^[7]

${\displaystyle \arccos \left(-{\sqrt {\frac {2}{3}}}\right)\approx 2.52611294\approx 144.735610^{\circ }}$

位於同個側錐側面的交角角度為負三分之一的反餘弦值，約為109.471度：^[7]

${\displaystyle \arccos \left(-{\frac {1}{3}}\right)\approx 1.9106332\approx 109.471221^{\circ }}$

頂點座標

三側錐三角柱的頂點座標為：^[2]

${\displaystyle \left(\pm {\frac {1}{2}},\,\pm {\frac {1}{2}},\,0\right)}$

${\displaystyle \left(0,\,0,\,{\frac {\sqrt {2}}{2}}\right)}$

${\displaystyle \left(0,\,\pm {\frac {1}{2}},\,-{\frac {\sqrt {3}}{2}}\right)}$

${\displaystyle \left(\pm {\frac {1+{\sqrt {6}}}{4}},\,0,\,-{\frac {{\sqrt {2}}+{\sqrt {3}}}{4}}\right)}$

最後一個座標的x和z值可透過解下列方程式獲得：^[2]

${\displaystyle x^{2}+\left({\frac {1}{2}}\right)^{2}+\left(z+{\frac {\sqrt {3}}{2}}\right)^{2}=1^{2}}$

${\displaystyle \left(x-{\frac {1}{2}}\right)^{2}+\left({\frac {1}{2}}\right)^{2}+z^{2}=1^{2}}$

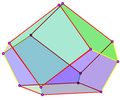
對偶多面體

三側錐三角柱的對偶多面體為截四階角雙三角錐（order-4 truncated triangular bipyramid），又稱底面截角雙三角錐（base-truncated triangular bipyramid）^[9]或5階結合多面體（英語：Associahedron）。

參見

• 詹森多面體
• 正四角錐
• 側錐三角柱
• 二側錐三角柱
• 多面體

參考文獻

1. Montroll, J. A Constellation of Origami Polyhedra. Dover Origami Papercraft Series. Dover Publications. 2004. ISBN 9780486439587. LCCN 2004056139.
2. Weisstein, Eric W. (編). Triaugmented Triangular Prism. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英語）.
3. Johnson, Norman W., Convex polyhedra with regular faces, Canadian Journal of Mathematics（英語：Canadian Journal of Mathematics）, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8
4. David I. McCooey. Johnson Solids: Triaugmented Triangular Prism. [2022-09-07]. （原始內容存檔於2021-05-07）.
5. The Triaugmented Triangular Prism. qfbox.info. [2022-09-08]. （原始內容存檔於2022-09-07）.
6. Triaugmented Triangular Prism. polyhedra.tessera.li.
7. Richard Klitzing. Triaugmented Triangular Prism, tautip. bendwavy.org. [2022-09-08]. （原始內容存檔於2021-09-24）.
8. Wolfram, Stephen. "Triaugmented Triangular Prism". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英語）.
9. Melker, Alexander I and Lonch, Vadim. Atomic and electronic structure of mini-fullerenes: from four to twenty (PDF). materials Physics and mechanics (Федеральное государственное бюджетное учреждение науки Институт проблем~…). 2012, 13 (1): 22–36 [2022-09-08]. （原始內容存檔 (PDF)於2022-03-15）.

外部連結

• 埃里克·韋斯坦因. Johnson Solid. MathWorld.
• 埃里克·韋斯坦因. Triaugmented triangular prism. MathWorld.