法拉第弔詭

法拉第弔詭，或法拉第悖論（Faraday paradox）是一個關於法拉第感應定律的物理實驗。1831年，物理學家麥可·法拉第推斷出法拉第感應定律（簡稱「法拉第定律」），但是，在應用這定律來解釋法拉第弔詭的過程中，他遇到了很多困難。這在本文會有詳細相關敘述。

麥可·法拉第

實驗組態

參見：發電機

圖1，法拉第的圓盤形發電機。圓盤形導體（淺藍色）以角速率 ${\displaystyle \omega }$ 旋轉於由一塊圓柱形永久磁鐵（未繪出）產生的磁場 ${\displaystyle \mathbf {B} }$ （以棕褐色箭矢表示）。勞侖茲力的磁部分 ${\displaystyle \mathbf {v} \times \mathbf {B} }$ 趨動徑向電流，從圓盤中心，流過圓盤，抵達邊緣（天藍色），然後通過底端金屬刷（五角形）、支撐架（深藍色）、轉軸，返回圓盤中心，形成完整迴路。只要轉動圓盤，就可以從機械運動產生電流（金黃色）。

如右圖所示，法拉第弔詭實驗只需要一些簡單器件：圓柱形永久磁鐵、圓盤形導體、金屬刷、轉軸導體、支撐架導體，檢流計。圓柱形永久磁鐵與圓盤形導體分別安裝於各自的轉軸，可以各自自由旋轉。將安裝於支撐架一端的金屬刷與圓盤邊緣相接觸，又將與圓盤相連接的轉軸安裝於支撐架另一端，就可以形成完整閉合電路。在這閉合電路中，串聯一個檢流計來測量電流。

實驗程序

這實驗的進行有三個步驟：

1. 假設磁鐵為固定不動，不能旋轉，只讓圓盤旋轉，則檢流計會測量到直流。這實驗設備的功能類似發電機，因此稱為「法拉第發電機」、法拉第圓盤、或單極發電機（英語：homopolar generator）。
2. 假設圓盤為固定不動，不能旋轉，只讓磁鐵旋轉，則檢流計不會測量到直流。
3. 假設讓圓盤與磁鐵以同角速度旋轉，則檢流計會測量到直流，如同第一步驟得到的結果。

為什麼弔詭？

有些物理學者稱這實驗為弔詭，因為，猛然一看，這實驗似乎違背了法拉第定律，不論是甚麼部分在旋轉，穿過圓盤的磁通量好像都一樣，所以，從磁通量觀點來看，對於這三個案例，電動勢都應該預測為零。這觀點錯誤地選擇了用來計算磁通量的曲面，對於這論點，稍後會有更詳細解釋。

透過鐵粉顯示出的磁場線。將條狀磁鐵放在白紙下面，鋪灑一堆鐵粉在白紙上面，這些鐵粉會依著磁場線的方向排列，形成一條條的曲線，在曲線的每一點顯示出磁場線的方向。

從磁場線觀點來看，這弔詭又有不同的理論結果。在法拉第的電磁感應模型裏，磁場是由想像的磁場線組成。若將條狀磁鐵放在白紙下面，鋪灑一堆鐵粉在白紙上面，這些鐵粉會依著磁場線的方向排列，形成一條條的曲線，在曲線的每一點顯示出磁場線的方向。假若電動勢與磁場線被電路切割的速率呈正比，則從磁鐵的參考系觀測，磁場線為固定不動。所以，相對於磁鐵，將圓盤旋轉，或相對於圓盤，將磁鐵旋轉，這兩種動作應該都會生成電動勢，但是若將磁鐵與圓盤一同旋轉，則電動勢為零。

法拉第的解釋

在法拉第的「電磁感應模型」裏，當閉合電路切割過磁場線時，會有感應電流生成於這閉合電路。按照這模型，當圓盤旋轉或磁鐵旋轉時，應該會有感應電流流動於法拉第圓盤，而當磁鐵與圓盤一同旋轉時，應該不會出現感應電流。然而，這結果與實驗結果迥然不同。法拉第試圖解釋這差異，他假定當磁鐵旋轉時，磁鐵的整個磁場於其伴隨的磁場線固定不動（注意到這是一個完全正確的繪景，雖然也許不太容易從電磁感應模型推理出來）。換句話說，磁場線的參考系與磁鐵的參考系不同。在下一個段落，會有詳細論述，現代物理學（自從發現電子之後）不需要電磁感應模型，就能夠完全解釋這弔詭。

現代解釋

電子與勞侖茲力

參見：勞侖茲力定律

自從約瑟夫·湯姆森於1897年發現電子之後，物理學者獲得了微觀解析這弔詭的能力。注意到移動於磁場 ${\displaystyle \mathbf {B} }$ 的電子會感受到勞侖茲力 ${\displaystyle \mathbf {F} _{Lorentz}=q\mathbf {v} \times \mathbf {B} }$ ；其中，${\displaystyle q}$ 是電子所帶電荷量，${\displaystyle \mathbf {v} }$ 是電子移動速度。如圖1所示，呈旋轉運動中的圓盤導體，其內部自由電子會感受到勞侖茲力。這勞侖茲力垂直於電子的速度 ${\displaystyle \mathbf {v} }$ ，也垂直於磁場 ${\displaystyle \mathbf {B} }$ ，而磁場 ${\displaystyle \mathbf {B} }$ 又垂直於圓盤。所以，按照右手定則，這勞侖茲力的方向（對於電子）是反徑向，即朝著轉軸的方向；對於正價粒子，勞侖茲力的方向是徑向，即朝著圓盤邊緣的方向。

當然，這徑向力會生成動生電動勢，造成電流流動於整個電路，因為它造成了電子的反徑向移動。這電子的反徑向運動又會生成另一股勞侖茲力，反抗隨著圓盤旋轉的電子圓周運動，這趨向於使圓盤旋轉變慢。因此，只有倚賴不斷地施加外力，圓盤才能持續旋轉。由於圓盤持續旋轉，電流也持續地流動於整個電路。這機制與實驗觀測相符合：每當圓盤旋轉，就會生成電流，不論磁場的屬性為何。

應用勞侖茲力定律可以解釋法拉第弔詭，但這也在學術界引起極大的爭論──到底磁場是否隨著磁鐵旋轉？按照勞侖茲力定律，磁場與導體之間的相對運動，直接地與作用於電荷的勞侖茲力有關，物理學者猜測，對於磁鐵與圓盤共同旋轉而電動勢不為零的案例，磁場應該不會與磁鐵共同旋轉，否則，磁場就無法與圓盤呈相對運動。

數學分析

參見：法拉第感應定律

對於從金屬刷，經過支撐架與轉軸，到圓盤中心這一段路徑，由於磁場與這路徑的包含平面之間互相平行，而不是互相正交，不論是甚麼器件在旋轉，路徑積分獲得的電動勢永遠為零。因此，只需要專注於從圓盤中心到金屬刷這一段路徑。

法拉第定律表明，^[1]

任何閉合電路中感應電動勢的大小，等於穿過這電路的磁通量的變化率。

以方程式表示，

${\displaystyle {\mathcal {E}}=-{\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} t}}=-{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{\Sigma (t)}\mathbf {B} (\mathbf {r} ,\ t)\cdot \mathrm {d} \mathbf {a} }$ ；

其中，${\displaystyle {\mathcal {E}}}$ 是電動勢，${\displaystyle \Phi _{B}}$ 是磁通量，${\displaystyle \mathbf {B} }$ 是磁場，${\displaystyle \Sigma (t)}$ 是以閉合電路為邊緣的任意積分曲面，${\displaystyle \mathrm {d} \mathbf {a} }$ 是微小面元素。

圖2，用來計算電動勢的兩條可行迴路。在圓盤區域，金色的幾何簡單迴路比較容易使用，但另外一條黃色迴路會給出同樣結果。在選擇這兩條迴路時，並不存在想要模仿任何實際電流路徑的意圖。

怎樣才能應用這定律於法拉第圓盤發電機？一種方法是定義「磁通切割率」，首先繪一條假想線於圓盤，從金屬刷到轉動軸，然後，計算這條假想線切割過多少磁通量每單位時間。如圖2所示，假定圓盤半徑為 ${\displaystyle R}$ ，則其圓心角為 ${\displaystyle \theta }$ 的扇形部分的面積 ${\displaystyle a}$ 為

${\displaystyle a={\frac {\theta }{2\pi }}\pi R^{2}}$ ，

這假想線的磁通切割率為

${\displaystyle B\ {\frac {\mathrm {d} a}{\mathrm {d} t}}=-{\frac {BR^{2}}{2}}\ {\frac {\mathrm {d} \theta }{\mathrm {d} t}}=-{\frac {BR^{2}\omega }{2}}}$ ；

其中，${\displaystyle \omega }$ 為圓盤旋轉的角速率。

將法拉第定律內的磁通量變化率更改為磁通切割率，其它內容不變。根據這更改的法拉第定律，電動勢為

${\displaystyle {\mathcal {E}}=-{\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} t}}=-B\ {\frac {\mathrm {d} a}{\mathrm {d} t}}={\frac {BR^{2}\omega }{2}}}$ 。

注意到在思考電動勢（或電流）的方向時，需要基於冷次定律，運動所生成的電動勢必會抗拒由於運動而產生的磁通量。例如，在圖2中的金色迴路，其處於圓盤的徑向線段（假想線），所切割過的扇面，假設這扇面向量與磁場相向，則磁通量為正值，並且隨著時間演進而增加。根據冷次定律，感應的電動勢（因此電流）趨向於削減磁通量。按照右手定則，假想線內的電動勢（或電流）的方向為徑向。

這從計算切割磁通量所得到的電動勢結果，可以與從假想線移動於磁場所感應出的動生電動勢相比較：

${\displaystyle {\mathcal {E}}={\frac {F_{Lorentz}}{q}}=\int _{0}^{R}Br\omega \mathrm {d} r={\frac {BR^{2}\omega }{2}}}$ ；

其中，${\displaystyle F_{Lorentz}}$ 是勞侖茲力。

兩個答案相同。處於假想線的正電荷，所感受到的勞侖茲力的方向為${\displaystyle \mathbf {v} \times \mathbf {B} }$ 的方向，即徑向。

對於這計算電路所切割的磁通量的方法，若要嚴格地以法拉第定律做形式化處理，必需正確地計算被閉合電路圍入的曲面 ${\displaystyle \Sigma (t)}$ 。當然，假若積分的區域與時間有關，則取這積分的時間微分並不能簡單地只取其被積函數的時間微分，這一點時常會被忽略。詳細計算方法，請參閱萊布尼茨積分定則（Leibniz integral rule）與勞侖茲力定律。

在選擇曲面 ${\displaystyle \Sigma (t)}$ 時，有兩個限制：

1. 這曲面必需被閉合迴路圍入，而這閉合迴路是想要計算電動勢之處。
2. 這曲面必需捕獲到電路的所有移動部分的相對運動。

再度強調一次，閉合迴路不需要對應於實際電流的流動路徑。電磁感應倚賴的是相對運動，閉合迴路必需捕獲所有相對運動。對於圖1所示案例，因為電流流動迴路的一部分分佈於空間的某區域，有很多條可能迴路可以選來計算趨動電流的電動勢。圖2展示出兩條可能迴路。所有的可能迴路必需包括回程路徑，但是在圓盤區域，展示出兩條可能路徑：一條是幾何簡單路徑，另一條是迂迴曲折路徑。選擇哪一條路徑乃見仁見智之舉。但是，一旦做出選擇，就不能在計算中更改路徑，必需使用固定於圓盤的同樣路徑，跟著圓盤一同旋轉，計算切割過的磁通量。

圖3，法拉第圓盤被映射為滑動的長方形導體。圓盤被視為圓環，沿著半徑切開，然後彎開為長方塊。

對於這案例，所有這些迴路獲得的磁通切割率都相同，因而電動勢也相同。為了幫助理解這路徑獨立的點子，如圖3所示，法拉第圓盤被展開為長方塊，使得這問題看起來好似滑動的長方塊問題。對於滑動的長方塊案例，很明顯地，在長方塊內部，電流流動的圖樣與時間無關，因此也與電路的磁通切割率無關。所以，不需要思考電流怎樣流過長方塊（或圓盤）。任意連結長方形頂部軌道與底部軌道（從轉軸經過圓盤到金屬刷）的路徑選擇，其隨著長方塊的移動（隨著圓盤的旋轉）會掃出同樣的磁通切割率，也會計算出同樣的電動勢。

更多觀察

磁鐵到底是否在旋轉，這事實對於本分析無關緊要，因為相關資料並沒有出現於法拉第感應定律。實際而言，假設磁鐵具有圓柱對稱性，則旋轉磁鐵絕不會改變電磁場。同樣地，將磁鐵與圓盤一起旋轉，或將圓盤旋轉而固定磁鐵不動，兩種方式得到的結果相同。關鍵是在於圓盤與回程導體之間的相對運動，而不是圓盤與磁鐵之間的相對運動。

為了清楚解釋這論點，將法拉第圓盤修改，將回程導體改為另外一個圓盤，也就是說，將兩個圓盤導體安裝於同一個轉軸，讓這兩個圓盤在轉軸與週邊都擁有電接觸點。則電流會與兩個圓盤的相對旋轉運動成正比，與磁鐵的任意旋轉無關。

法拉第感應定律不適用案例

圖4，根據費曼教科書的例子給出的案例。對於這案例，法拉第定律不適用。光電導體長方塊（淡藍色）沿著兩條平行導線滑行。在某狹窄固定區域（深藍色），照射強烈光波，施加強烈磁場。當長方塊行經這狹窄固定區域時，被照射到的材料會出現導電性質。由於勞侖茲力定律，整個電路會出現電動勢與電流（金黃色）。

如圖4所示，光電導體長方塊平移於兩條平行導線。在某狹窄固定區域，照射強烈光波，施加強烈磁場。當長方塊行經這狹窄固定區域時，被照射到的光電導體會出現導電性質。由於勞侖茲力定律，會有電流從頂方導線，經過這狹窄固定區域的光電導體，流動到底方導線，然後經過連接電路，回到頂方導線。對於這案例，電路固定不動，穿過電路的磁通量不變，所以，應用法拉第定律計算出來的電流為零。但是，勞侖茲力定律建議，電流實際存在。

這案例是根據物理大師理查·費曼想出來的點子，凸顯法拉第定律（即連結電動勢與磁通量之間的關係的版本，費曼稱為「通量定則」）不適用於某些狀況的事實。費曼這樣說：^[2]

對於這案例，通量定則不適用。通量定則只能應用於一類電路，其路徑的實體物質不能改變。假若電路路徑的實體物質有所改變，則必須回到基本定律。以下兩個基本定律永遠會給出正確的物理

${\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} )}$ 、

${\displaystyle \nabla \times \mathbf {E} =-{\begin{matrix}{\frac {\partial }{\partial t}}\end{matrix}}\mathbf {B} }$ 。
— 理查·費曼 《費曼物理學講義》

費曼應用勞侖茲定律來解釋為何會出現這種現象。重點是通量定則只適用於某些狀況，雖然這些是非常實用的狀況。

狹義相對論的解釋

假若應用狹義相對論，就不會遭遇任何弔詭或困擾。思考狹窄固定區域的參考系 ${\displaystyle S}$ ，對於處於這參考系 ${\displaystyle S}$ 的觀測者而言，光電導長方塊以速度 ${\displaystyle v}$ 移動。恰巧處於狹窄固定區域的光電導物質，由於被強烈光波照射，會變得具有導電性質，其載有電量 ${\displaystyle q}$ 的載電粒子會感受到勞侖茲力 ${\displaystyle F_{Lorentz}=qvB}$ 。

換到光電導長方塊的參考系 ${\displaystyle S'}$ 。對於處於參考系 ${\displaystyle S'}$ 的觀測者而言，光電導長方塊是固定不動，狹窄光波照射區域是以速度 ${\displaystyle -v}$ 移動，磁場為 ${\displaystyle B'=\gamma B}$ ，電場為 ${\displaystyle E'=\gamma vB}$ ；其中，${\displaystyle \gamma =1/{\sqrt {1-v^{2}/c^{2}}}}$ 是勞侖茲因子。所以，其載有電量 ${\displaystyle q}$ 的載電粒子會感受到勞侖茲力 ${\displaystyle F_{Lorentz}'=qE'=q\gamma vB}$ 。

注意到從參考系 ${\displaystyle S}$ 變換到參考系 ${\displaystyle S'}$ ，勞侖茲的變換為

${\displaystyle F'={\frac {F}{(1-v^{2}/c^{2})\gamma }}=\gamma F}$ 。

這與分別在參考系 ${\displaystyle S}$ 與 ${\displaystyle S'}$ 推導出來的勞侖茲力表達式相符合。^[3][4]

倜立實驗

倜立實驗電路圖

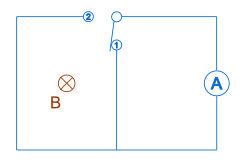
通量定則不適用於倜立實驗。圖5展示「倜立實驗」。^[5]在這由物理學者唐納德·倜立（Donald Tilley）設計出的實驗裏，整個電路是由兩個迴路或網目組成。在右手邊迴路串聯了一具檢流計。在左手邊迴路中心置放了一塊磁鐵，其產生的磁場為 ${\displaystyle \mathbf {B} }$ 。兩個迴路共同享有一個轉閘開關。首先設定轉閘開關與端點1相接觸，左手邊迴路為開路，右手邊迴路為閉路。然後旋轉轉閘開關，改與端點2相接觸，使得右手邊迴路成為開路，左手邊迴路仍舊為開路，但整個電路成為閉路。注意到磁場並沒有改變，但是穿過的面積變大，因此，磁通量也會改變。可是，檢流計的量針並沒有偏動（假定可以忽略轉閘開關旋轉時的效應），這意味著檢流計並沒有檢測到任何感應電動勢。所以，法拉第定律不適用於這案例。

有些物理學者認為，在法拉第實驗裏，感應電壓的出現，是因為電路切割了磁場線，而不是因為實際磁通量有所變化。這可以從倜立實驗觀察得知，因為，雖然穿過電路的磁通量有所變化，並沒有任何磁場線移動經過電路，所以不會有任何感應電流。

物理學者艾倫·納斯邦（Allen Nussbaum）建議，只有在磁通量改變的時候，同時也給出機械功，法拉第定律才適用。^[6]思考處於磁場 ${\displaystyle \mathbf {B} }$ 、載有電流 ${\displaystyle I}$ 的載流導線，其所感受到的作用力可以表達為

${\displaystyle \mathrm {d} \mathbf {F} =I\mathrm {d} {\boldsymbol {\ell }}\mathbf {\times } \mathbf {B} }$ ；

其中，${\displaystyle \mathrm {d} \mathbf {F} }$ 是載流導線所感受到的微小作用力，${\displaystyle \mathrm {d} {\boldsymbol {\ell }}}$ 是載流導線的微小線元素。

假設微小線元素 ${\displaystyle \mathrm {d} {\boldsymbol {\ell }}}$ 的位移為 ${\displaystyle \mathrm {d} \mathbf {r} }$ ，則所做的機械功 ${\displaystyle \mathrm {d} W}$ 為

${\displaystyle \mathrm {d} W=\mathrm {d} \mathbf {F} \cdot \mathrm {d} \mathbf {r} =(I\mathrm {d} {\boldsymbol {\ell }}\mathbf {\times } \mathbf {B} )\cdot \mathrm {d} \mathbf {r} }$ 。

微小線元素 ${\displaystyle \mathrm {d} {\boldsymbol {\ell }}}$ 因為位移而遮蓋的面積 ${\displaystyle \mathrm {d} \mathbf {S} }$ 為

${\displaystyle \mathrm {d} \mathbf {S} =\mathrm {d} \mathbf {r} \mathbf {\times } \mathrm {d} {\boldsymbol {\ell }}}$ ，

所做的機械功為

${\displaystyle \mathrm {d} W=I\mathbf {B} \cdot \mathrm {d} \mathbf {s} =I\mathrm {d} \Phi }$ ；

其中，${\displaystyle \Phi }$ 是磁通量。

這機械功等於電勢為 ${\displaystyle V}$ 的電荷 ${\displaystyle \mathrm {d} q}$ 的電勢能：

${\displaystyle \mathrm {d} W=V\mathrm {d} q=VI\mathrm {d} t}$ 。

這樣，可以得到法拉第定律的方程式：

${\displaystyle \mathrm {d} \mathbf {\Phi } =V\mathrm {d} t}$ 。

注意到，法拉第定律的方程式為正確無誤，若且唯若，機械功 ${\displaystyle \mathrm {d} W}$ 不等於零。換句話說，只有倚賴做機械功來改變磁通量，法拉第定律才正確無誤。

回到倜立實驗。由於磁通量的改變並沒有做出機械功（假定扭轉轉閘開關所做的機械功為零），所以，法拉第定律不適用，不會出現任何電動勢或電流。

參考文獻

1. M N O Sadiku. Elements of Electromagnetics Fourth. NY/Oxford UK: Oxford University Press. 2007: §9.2 pp. 386 ff. ISBN 0-19-530048-3.
2. 費曼, 理查; 雷頓, 羅伯; 山德士, 馬修, 費曼物理學講義 II 電磁與物質(2)介電質、磁與感應定律, 台灣: 天下文化書: pp. 206–211, 2006, ISBN 978-986-216-231-6 引文格式1維護：冗餘文本 (link)
3. Griffiths, David J., Introduction to Electrodynamics (3rd ed.), Prentice Hall: pp. 516–532, 1998, ISBN 0-13-805326-X 引文格式1維護：冗餘文本 (link)
4. Hughes, William; Young, Frederick, The electromagnetodynamics of fluids, Wiley: pp. 31, 1966 引文格式1維護：冗餘文本 (link)
5. Tilley, Donald, Exceptions to the Flux Rule for Electromagnetic Induction, American Journal of Physics, 1968, 36 (5): 458
6. Nussbaum, Allen, Faraday's Law Paradoxes (PDF), Physics Education, 1972, 7 (4): 231, doi:10.1088/0031-9120/7/4/006

參閱

• 移動中的磁鐵與導體問題
• 經典電磁學與狹義相對論

進階閱讀

• Michael Faraday,Experimental Researches in Electricity, Vol I, First Series, 1831 in Great Books of the Western World, Vol 45, R. M. Hutchins, ed., Encyclopædia Britannica, Inc., The University of Chicago, 1952. [1] （頁面存檔備份，存於網際網路檔案館）
• "Electromagnetic induction: physics and flashbacks" (PDF) （頁面存檔備份，存於網際網路檔案館） by Giuseppe Giuliani －講述在法拉第圓盤裏，勞侖茲力的物理行為。
• P. J. Scanlon, R. N. Henriksen, and J. R. Allen, "Approaches to electromagnetic induction," Am. J. Phys. 37, 698–708 (1969). －描述怎樣應用法拉第定律於法拉第圓盤。
• Jorge Guala-Valverde, Pedro Mazzoni, Ricardo Achilles "The homopolar motor: A true relativistic engine," Am. J. Phys. 70 (10), 1052–1055 (Oct. 2002). －建議只有勞侖茲力定律可以解釋法拉第圓盤，描述一些關於這論點的實驗證據。
• Frank Munley, Challenges to Faraday's flux rule, Am. J. Phys. 72, 1478 (2004). －更近期的關於法拉第通量定則的論述。
• Richard Feynman, Robert Leighton, Matthew Sands, "The Feynman Lectures on Physics Volume II", Chapter 17 －解釋法拉第弔詭（磁通量不變，但有電動勢）與「搖擺導板弔詭」（磁通量改變，但沒有感應出電動勢）。
• W. F. Hughes and F. J. Young, The Electromagnetodynamics of Fluids, John Wiley & Sons (1965) LCCC #66-17631. Chapters 1. Principles of Special Relativity and 2. The Electrodynamics of Moving Media. －只要熟讀精通這兩章內容，就可以解析所有感應電動勢問題，並且解釋文獻裏找到的所有相關弔詭。