林-錢方程(Lin-Tsien equation)是林家翹-錢學森和創立的描述可壓縮流體中物體跨音速運動的非線性偏微分方程[1][2]

利用Maple中的軟件包TWS_solution可得林-錢方程的多種行波解[3]
u(x,y,t)=TWS_sol := {u(x, y, t) = _C1+(-(1/2)*ln(tanh(_C3+_C4*x+_C5*y+_C6*t)+1)+(1/2)*ln(tanh(_C3+_C4*x+_C5*y+_C6*t)-1))*_C2}
g[2] := {u(x, y, t) = _C1+arctan(1/\sqrt(csc(_C3+_C4*x+_C5*y+_C6*t)^2-1))*_C2}
g[2] := {u(x, y, t) = _C1+(-(1/2)*ln(coth(_C3+_C4*x+_C5*y+_C6*t)+1)+(1/2)*ln(coth(_C3+_C4*x+_C5*y+_C6*t)-1))*_C2}
g[2] := {u(x, y, t) = _C1+arctanh(1/\sqrt(1+csch(_C3+_C4*x+_C5*y+_C6*t)^2))*_C2}
找到了一個新的可積(3 + 1)維泛化; 見論文 [4]的系統(40)
 Lin-Tsien equation traveling wave plot Lin-Tsien equation traveling wave plot
|
 Lin Tsien eq TWS extended coth Lin Tsien eq TWS extended coth
|
 Lin Tsien eq TWS extended csch Lin Tsien eq TWS extended csch
|
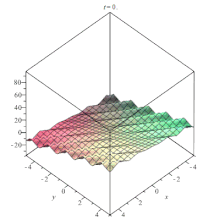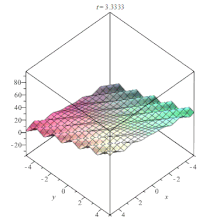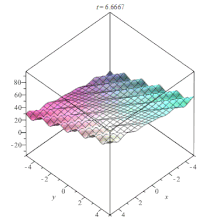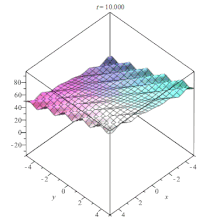
 Lin-Tsien nlpde animation Lin-Tsien nlpde animation
|
 Lin-Tsien nlpde 3d plot Lin-Tsien nlpde 3d plot
|
 Lin Tsien eq extended csc arctan Lin Tsien eq extended csc arctan
|
|

|
C.C. Lin, E.Reissner,and H.S.Tsien, On Two Dimensional Non-steady Motion of a Slender Body in a Compressible Fluid, 錢學森文集 p513 上海交通大學出版社
Graham W. Griffiths Willian Schiesser, Traveling wave analysis of Partial Differential Equations p436
- *谷超豪 《孤立子理論中的達布變換及其幾何應用》 上海科學技術出版社
- *閻振亞著 《複雜非線性波的構造性理論及其應用》 科學出版社 2007年
- 李志斌編著 《非線性數學物理方程的行波解》 科學出版社
- 王東明著 《消去法及其應用》 科學出版社 2002
- *何青 王麗芬編著 《Maple 教程》 科學出版社 2010 ISBN 9787030177445
- Graham W. Griffiths William E.Shiesser Traveling Wave Analysis of Partial Differential p135 Equations Academy Press
- Richard H. Enns George C. McCGuire, Nonlinear Physics Birkhauser,1997
- Inna Shingareva, Carlos Lizárraga-Celaya,Solving Nonlinear Partial Differential Equations with Maple Springer.
- Eryk Infeld and George Rowlands,Nonlinear Waves,Solitons and Chaos,Cambridge 2000
- Saber Elaydi,An Introduction to Difference Equationns, Springer 2000
- Dongming Wang, Elimination Practice,Imperial College Press 2004
- David Betounes, Partial Differential Equations for Computational Science: With Maple and Vector Analysis Springer, 1998 ISBN 9780387983004
- George Articolo Partial Differential Equations & Boundary Value Problems with Maple V Academic Press 1998 ISBN 9780120644759
- A. Sergyeyev, New integrable (3+1)-dimensional systems and contact geometry, Lett. Math. Phys. 108 (2018), no. 2, 359-376, https://arxiv.org/abs/1401.2122 (頁面存檔備份,存於網際網路檔案館)








