Loading AI tools
来自维基百科,自由的百科全书
在数学的数值分析领域中,贝兹曲线(英语:Bézier curve)是计算机图形学中相当重要的参数曲线。更高维度的广泛化贝兹曲线就称作贝兹曲面,其中贝兹三角是一种特殊的实例。

贝兹曲线于1962年,由法国工程师皮埃尔·贝兹(Pierre Bézier)所广泛发表,他运用贝兹曲线来为汽车的主体进行设计。贝兹曲线最初由保尔·德·卡斯特里奥于1959年运用德卡斯特里奥演算法开发,以稳定数值的方法求出贝兹曲线。
给定点P0、P1,线性贝兹曲线只是一条两点之间的直线。这条线由下式给出:
且其等同于线性插值。
二次方贝兹曲线的路径由给定点P0、P1、P2的函数B(t)追踪:
P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝兹曲线。曲线起始于P0走向P1,并从P2的方向来到P3。一般不会经过P1或P2;这两个点只是在那里提供方向资讯。P0和P1之间的间距,决定了曲线在转而趋进P2之前,走向P1方向的“长度有多长”。
曲线的参数形式为:
现代的成象系统,如PostScript、Asymptote和Metafont,运用了以贝兹样条组成的三次贝兹曲线,用来描绘曲线轮廓。
阶贝兹曲线可如下推断。给定点P0、P1、…、Pn,其贝兹曲线即
例如:
如上公式可如下递归表达: 用表示由点P0、P1、…、Pn所决定的贝兹曲线。则
用平常话来说,阶的贝兹曲线,即双阶贝兹曲线之间的插值。
一些关于参数曲线的术语,有
即多项式
又称作n阶的伯恩斯坦基底多项式,定义00 = 1。
点Pi称作贝兹曲线的控制点。多边形以带有线的贝兹点连接而成,起始于P0并以Pn终止,称作贝兹多边形(或控制多边形)。贝兹多边形的凸包(convex hull)包含有贝兹曲线。

|
| 线性贝兹曲线演示动画,t在[0,1]区间 |
线性贝兹曲线函数中的t会经过由P0至P1的B(t)所描述的曲线。例如当t=0.25时,B(t)即一条由点P0至P1路径的四分之一处。就像由0至1的连续t,B(t)描述一条由P0至P1的直线。
为建构二次贝兹曲线,可以中介点Q0和Q1作为由0至1的t:
 |
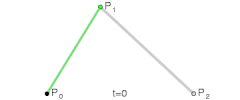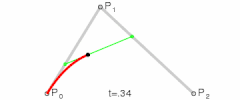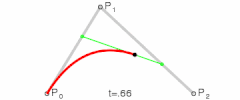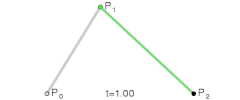
| |
| 二次贝兹曲线的结构 | 二次贝兹曲线演示动画,t在[0,1]区间 |
为建构高阶曲线,便需要相应更多的中介点。对于三次曲线,可由线性贝兹曲线描述的中介点Q0、Q1、Q2,和由二次曲线描述的点R0、R1所建构:
 |
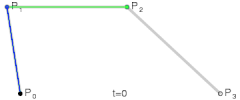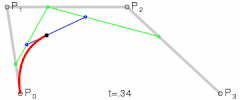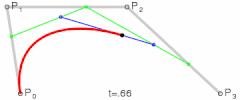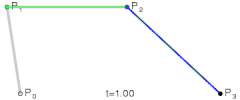
| |
| 三次贝兹曲线的结构 | 三次贝兹曲线演示动画,t在[0,1]区间 |
对于四次曲线,可由线性贝兹曲线描述的中介点Q0、Q1、Q2、Q3,由二次贝兹曲线描述的点R0、R1、R2,和由三次贝兹曲线描述的点S0、S1所建构:
 |
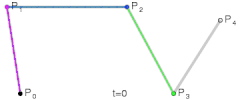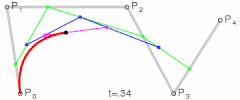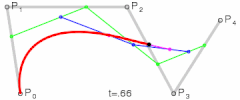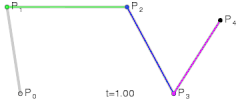
| |
| 四次贝兹曲线的结构 | 四次贝兹曲线演示动画,t在[0,1]区间 |
还可参阅五阶贝兹曲线的构成:

|
| 五次贝兹曲线演示动画,t在[0,1]区间 |
n次贝兹曲线可以转换为一个形状完全相同的n+1次贝兹曲线。 这在软体只支援特定阶次的贝兹曲线时很有用。 例如,Cairo只支援三次贝兹曲线,你就可以用升阶的方法在Cairo画出二次贝兹曲线。
我们利用这个特性来做升阶。我们把曲线方程式中每一项都乘上 (1 − t) 或 t,让每一项都往上升一阶。以下是将二阶升为三阶的范例
对任何的n值,我们都可以使用以下等式
式中 和 可以任意挑选。
因此,新的控制点为[2]
由于需要点阵化更精细的解析度时,重新插值(补点)的计算量较小,贝兹曲线被广泛地在计算机图形中用来为平滑曲线建立模型。贝兹曲线是矢量图形文件和相应软件(如PostScript、PDF等)能够处理的唯一曲线,用于光滑地近似其他曲线。
二次和三次贝兹曲线最为常用。
下列程式码为一简单的实际运用范例,展示如何使用C语言标出三次方贝兹曲线。注意,此处仅简单的计算多项式系数,并读尽一系列由0至1的t值;实践中一般不会这么做,递归求解通常会更快速——以更多的记忆体为代价,花费较少的处理器时间。不过直接的方法较易于理解并产生相同结果。以下程式码已使运算更为清晰。实践中的最佳化会先计算系数一次,并在实际计算曲线点的回圈中反复使用。此处每次都会重新计算,损失了效率,但程式码更清楚易读。
曲线的计算可在曲线阵列上将相连点画上直线——点越多,曲线越平滑。
在部分架构中,下以程式码也可由动态规划进行最佳化。举例来说,dt是一个常数,cx * t则等同于每次反复就修改一次常数。经反复应用这种最佳化后,回圈可被重写为没有任何乘法(虽然这个过程不是稳定数值的)。
/*
產生三次方貝茲曲線的程式碼
*/
typedef struct
{
float x;
float y;
}
Point2D;
/*
cp在此是四個元素的陣列:
cp[0]為起始點,或上圖中的P0
cp[1]為第一個控制點,或上圖中的P1
cp[2]為第二個控制點,或上圖中的P2
cp[3]為結束點,或上圖中的P3
t為參數值,0 <= t <= 1
*/
Point2D PointOnCubicBezier( Point2D* cp, float t )
{
float ax, bx, cx;
float ay, by, cy;
float tSquared, tCubed;
Point2D result;
/*計算多項式係數*/
cx = 3.0 * (cp[1].x - cp[0].x);
bx = 3.0 * (cp[2].x - cp[1].x) - cx;
ax = cp[3].x - cp[0].x - cx - bx;
cy = 3.0 * (cp[1].y - cp[0].y);
by = 3.0 * (cp[2].y - cp[1].y) - cy;
ay = cp[3].y - cp[0].y - cy - by;
/*計算位於參數值t的曲線點*/
tSquared = t * t;
tCubed = tSquared * t;
result.x = (ax * tCubed) + (bx * tSquared) + (cx * t) + cp[0].x;
result.y = (ay * tCubed) + (by * tSquared) + (cy * t) + cp[0].y;
return result;
}
/*
ComputeBezier以控制點cp所產生的曲線點,填入Point2D結構的陣列。
呼叫者必須分配足夠的記憶體以供輸出結果,其為<sizeof(Point2D) numberOfPoints>
*/
void ComputeBezier( Point2D* cp, int numberOfPoints, Point2D* curve )
{
float dt;
int i;
dt = 1.0 / ( numberOfPoints - 1 );
for( i = 0; i < numberOfPoints; i++)
curve[i] = PointOnCubicBezier( cp, i*dt );
}
另一种贝兹曲线的应用是在动画中,描述物件的运动路径等等。此处,曲线的x、y位置不用来标示曲线,但用来表示图形位置。当用在这种形式时,连续点之间的距离会变的更为重要,且大多不是平均比例。点将会串的更紧密,控制点更接近每一个点,而更为稀疏的控制点会散的更开。如果需要线性运动速度,进一步处理时就需要循所需路径将点平均分散。
有时我们可能想要把贝兹曲线表示为多项式,而非比较不直接的伯恩斯坦多项式。使用二项式定理和贝兹曲线的定义,重新整理后可以得到:
此处
计算曲线上的点时需要多次计算,因此事先计算好会比较实际;然而要小心高阶曲线可能会缺乏数值稳定性(需使用德卡斯特里奥算法来处理)。注意其空积为1。

有理贝兹增加可调节的权重,以提供更近似于随意的形状。分子是加权的伯恩斯坦形式贝兹曲线,而分母是加权的伯恩斯坦多项式的总和。
给定n + 1控制点Pi,有理贝兹曲线可如下描述:
或简单的
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.