安培环路定律

安培环路定律^[1]（英语：Ampère's circuital law）常直接简称为“安培定律”，是由安德烈-马里·安培于1826年提出的一条静磁学基本定律。

此条目页的主题是载流导线与其产生的磁场之间的关系。关于描述两条载流导线相互作用的力的定律，请见“安培力定律”。

本条目中，向量与标量分别用粗体与斜体显示。例如，位置向量通常用 ${\displaystyle \mathbf {r} \,\!}$ 表示；而其大小则用 ${\displaystyle r\,\!}$ 来表示。

安德烈-马里·安培。

安培环路定律表明了：在真空中载流导线所载有的稳恒电流，与磁感应强度沿著环绕导线的任意闭合回路（环路，closed loop）^{[注 1]}的路径积分（环场积），两者之间的关系为

${\displaystyle \oint _{\mathbb {C} }\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\mu _{0}I_{\text{enc}}}$；

其中，${\displaystyle \mathbb {C} }$是环绕著导线的闭合回路，${\displaystyle \mathbf {B} }$是磁感应强度（又称为B场），${\displaystyle \mathrm {d} {\boldsymbol {\ell }}}$是微小线元素向量，${\displaystyle \mu _{0}}$是磁常数，${\displaystyle I_{\text{enc}}}$是闭合回路${\displaystyle \mathbb {C} }$所围住的电流。

亦即，在真空中的稳恒电流会产生稳恒磁场，而磁感应强度B沿任意环绕载流导线的闭合路径的线积分值（环场积），等于该选取的环路（安培环路）所包围的总电流值（各个电流的代数和）乘以真空磁导率。

1861年，詹姆斯·马克士威又将这方程式重新推导一遍，使得符合电动力学条件，并且发表结果于论文《论物理力线》内。马克士威认为，含时电场会生成磁场，假若电场含时间，则前述安培定律方程式不成立，必须加以修正。经过修正后，新的方程式称为马克士威-安培方程式，是马克士威方程组中的一个方程式，以积分形式表示为

${\displaystyle \oint _{\mathbb {C} }\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\mu _{0}\int _{\mathbb {S} }\left(\mathbf {J} +{\frac {\partial \mathbf {D} }{\partial t}}\right)\cdot \mathrm {d} \mathbf {a} }$；

其中，${\displaystyle \mathbb {S} }$是边缘为${\displaystyle \mathbb {C} }$的任意曲面，${\displaystyle \mathbf {J} }$是穿过曲面${\displaystyle \mathbb {S} }$的电流的电流密度，${\displaystyle \mathbf {D} }$是电位移，${\displaystyle \mathrm {d} \mathbf {a} }$是微小面元素向量。

右手定则

载流回圈所产生的磁场方向可以使用右手定则来判断。其方法为将拇指外的四根手指向手掌弯的方向视为磁场方向，则拇指所指的方向即为电流的方向。

安培右手定则：将右手的大拇指指向电流${\displaystyle I}$方向，再将四根手指握紧电线，则弯曲的方向决定磁场${\displaystyle \mathbf {B} }$的方向

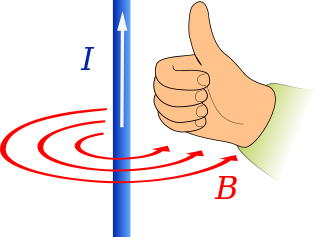
右手定则也可以用来辨明一条电线四周磁场的方向。对于这用法，右手定则称为“安培右手定则”，或“安培定则”。如右图，安培右手定则表明，假若将右手的大拇指朝著电线的电流方向指去，再将四根手指握紧电线，则四根手指弯曲的方向为磁场的方向。

原版安培环路定律

一条载流导线所载有的电流会产生磁场。

安培环路定律的历史原版形式，连结了磁场与源电流。这定律可以写成两种形式，积分形式和微分形式。根据克耳文－斯托克斯定理（即ℝ³上的斯托克斯公式），对于任意向量${\displaystyle \mathbf {F} }$，

${\displaystyle \int _{\mathbb {S} }\nabla \times \mathbf {F} \cdot \mathrm {d} \mathbf {a} =\oint _{\mathbb {C} }\mathbf {F} \cdot \mathrm {d} {\boldsymbol {\ell }}}$。

所以，这两种形式是等价的。

积分形式

电流${\displaystyle I}$在一个曲面${\displaystyle \mathbb {S} }$上的通量，等于磁场${\displaystyle \mathbf {B} }$沿著${\displaystyle \mathbb {S} }$的边缘闭合回路${\displaystyle \mathbb {C} }$的路径积分。采用国际单位制（后面会讲述CGS单位制版本），原版安培环路定律的积分形式可以写为^[2]：

${\displaystyle \oint _{\mathbb {C} }\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\mu _{0}I}$。

请注意到这方程式有些模糊之处，需要特别澄清：

• 第一，边界曲线${\displaystyle \mathbb {C} }$的正向与曲面${\displaystyle \mathbb {S} }$的侧符合右手规则。^{[注 1]}

• 第二，（固定${\displaystyle \mathbb {C} }$，）定理之成立与以${\displaystyle \mathbb {C} }$为边界的${\displaystyle \mathbb {S} }$的选择无关。^{[注 2]}

安培环路定律可由必欧-沙伐定律和磁场的叠加性证明（请参阅必欧-沙伐定律）。在静磁学中，安培环路定律的角色与高斯定律在静电学的角色类似。当系统组态具有适当的对称性时，我们可以利用这对称性，使用安培环路定律来便利地计算磁场。例如，当计算一条直线的载流导线或一个无限长螺线管的磁场时，可以采用圆柱坐标系来匹配系统的圆柱对称性。

微分形式

根据克耳文－斯托克斯定理，这方程式也可以写为微分形式。只有当电场不含时间的时候，也就是说，当电场对于时间的偏微分等于零的时候，这方程式才成立。采用国际单位制，这方程式表示为

${\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {J} }$。

磁场${\displaystyle \mathbf {B} }$的旋度等于（产生该磁场的）传导电流密度${\displaystyle \mathbf {J} }$。

电流分类

电流可以细分为自由电流和束缚电流，而束缚电流又可分类为磁化电流和电极化电流。以方程式表示，总电流密度${\displaystyle \mathbf {J} }$是

${\displaystyle \mathbf {J} =\mathbf {J_{f}+J_{M}+J_{P}} }$；

其中，${\displaystyle \mathbf {J} _{f}}$是自由电流密度或传导电流密度，${\displaystyle \mathbf {J} _{M}}$是磁化电流密度，${\displaystyle \mathbf {J} _{P}}$是电极化电流密度。

从微观而言，所有的电流基本上是一样的。但是，由于实用原因，物理学家会将电流分类为自由电流和束缚电流，对于每一类电流有不同的处理方式。例如，束缚电流通常发生于原子尺寸。物理学家或许想要使用较简单但适用于较大尺寸状况的理论。因此，较微观的安培定律，以B场${\displaystyle \mathbf {B} }$和微观电流（包括自由电流和束缚电流）来表达的定律，有时候会被替代为等价的形式，以附属磁场（又称为H场）${\displaystyle \mathbf {H} }$和自由电流来表达的形式。后面证明段落，会有详细的关于自由电流和束缚电流的定义，与两种表述等价的证明。

自由电流

通常在教科书内所提及的单独的“电流”二字，都是指的自由电流，即自由载流子（电子及阴阳离子）的定向移动。例如，通过一条导线或一个电池的电流。自由电流与后面提到的束缚电流明显不同，后者出现于可以被磁化或电极化的宏观物质里（每一种物质都会或多或少地被电极化或磁化）。

磁化电流

当一个物质被磁化的时候（例如，将此物质置入外磁场），电子仍旧会束缚于它们所属的原子。但是，它们的物理行为会有所改变（会与感受到的磁场耦合），产生微观电流。将这些电流总合在一起，会有如同宏观电流一般的效应，环绕于磁化物体内部或表面。称这电流为磁化电流，是束缚电流的一部分。称磁化电流的密度为“体磁化电流密度”${\displaystyle \mathbf {J} _{M}}$，用方程式定义为

${\displaystyle \mathbf {J} _{M}\ {\stackrel {def}{=}}\ \nabla \times \mathbf {M} }$；

其中，${\displaystyle \mathbf {M} }$是磁化强度（单位体积的磁偶极矩）。

电极化电流

束缚电流的另外一种来源是电极化电流。感受到电场的作用，可电极化物质内的正束缚电荷和负束缚电荷会以原子距离相互分离。假设电场随著时间而变化，束缚电荷也会随著时间而移动，因而产生“电极化电流”，称其密度为“电极化电流密度”${\displaystyle \mathbf {J} _{P}}$，用方程式定义为

${\displaystyle \mathbf {J} _{P}\ {\stackrel {def}{=}}\ {\frac {\partial \mathbf {P} }{\partial t}}}$；

其中，${\displaystyle \mathbf {P} }$是电极化强度。

注意到电极化强度的定义式

${\displaystyle \nabla \cdot \mathbf {P} \ {\stackrel {def}{=}}\ -\rho _{b}}$；

其中，${\displaystyle \rho _{b}}$是“体束缚电荷密度”。

取电极化电流密度的散度：

${\displaystyle \nabla \cdot \mathbf {J} _{P}={\frac {\partial }{\partial t}}(\nabla \cdot \mathbf {P} )}$。

所以，电极化电流密度与体束缚电荷密度的关系为

${\displaystyle \nabla \cdot \mathbf {J} _{P}=-{\frac {\partial \rho _{b}}{\partial t}}}$。

原版安培环路定律的不足处

原版安培环路定律只适用于静磁学。在电动力学里，当物理量含时间，有些细节必须仔细检查。思考安培方程式，

${\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {J} }$；

其中，${\displaystyle \mathbf {B} }$是B场，${\displaystyle \mu _{0}}$是磁常数，${\displaystyle \mathbf {J} }$是总电流。

取散度于这方程式，则会得到

${\displaystyle \nabla \cdot (\nabla \times \mathbf {B} )=\mu _{0}\nabla \cdot \mathbf {J} }$。

应用一个向量恒等式，旋度的散度必定等于零。所以，

${\displaystyle \nabla \cdot (\nabla \times \mathbf {B} )=0}$。

这意味著电流密度的散度等于零：

${\displaystyle \nabla \cdot \mathbf {J} =0}$。

在静磁学内，这是正确的。但是，出了静磁学范围，当电流不稳定的时候，这就不一定正确了。

一个正在充电的电容器，左边的圆形金属板，被一个假想的封闭圆柱表面${\displaystyle \mathbb {S} }$包围。这圆柱表面的右边表面${\displaystyle \mathbb {R} }$处于电容器的两块圆形金属板之间，左边表面${\displaystyle \mathbb {L} }$处于最左边。没有任何传导电流通过表面${\displaystyle \mathbb {R} }$，而有电流${\displaystyle I}$通过表面${\displaystyle \mathbb {L} }$。

举个经典例子，如图右，一个正在充电的电容器，其两片金属板会随著时间分别累积异性电荷。设定表面${\displaystyle \mathbb {L} }$的边缘为闭合回路${\displaystyle \mathbb {C} }$。应用安培定律，

${\displaystyle \oint _{\mathbb {C} }\mathbf {B} \cdot d{\boldsymbol {\ell }}=\mu _{0}I_{\text{enc}}}$。

在这里，${\displaystyle I_{\text{enc}}}$是通过任意曲面的电流，只要这曲面符合一个条件：边缘为闭合回路${\displaystyle \mathbb {C} }$。所以，这任意曲面可以是表面${\displaystyle \mathbb {L} }$，而${\displaystyle I_{\text{enc}}}$是${\displaystyle I}$；或者这任意曲面可以是封闭圆柱表面减去左边表面${\displaystyle \mathbb {S} -\mathbb {L} }$，而由于通过这任意曲面的电流是${\displaystyle 0}$，${\displaystyle I_{\text{enc}}}$是${\displaystyle 0}$。选择不同的曲面会得到不同的答案，这在物理学里，是绝对不允许发生的事。

为了解决上述难题，安培环路定律必须加以修改延伸。应用流体力学的方法，马克士威摹想磁场为电介质涡旋（vortex）大海，而位移电流即为大海内的电极化电流^[3]。在他于1861年发表的论文《论物理力线》里面，马克士威将位移电流项目加入了安培定律^[4]。

位移电流

主条目：位移电流

在自由空间内，位移电流跟电场随著时间的变化率有关；而在电介质内，上述贡献仍旧存在，但另外一个重要贡献则与电介质的电极化有关。虽然电荷不能自由地运动于电介质，感受到外电场的作用，分子的束缚电荷可以做微小的运动。因此，正值和负值的束缚电荷会产生小距离的分离，造成电极化的增加，这可以用变量电极化强度${\displaystyle P}$来表达。电极化强度随著时间的变化所产生的效应就是电极化电流。

位移电流密度${\displaystyle \mathbf {J} _{D}}$定义为^[2]

${\displaystyle \mathbf {J} _{D}\ {\stackrel {def}{=}}\ {\frac {\partial \mathbf {D} }{\partial t}}}$；

其中，${\displaystyle \mathbf {D} }$是电位移，定义为

${\displaystyle \mathbf {D} \ {\stackrel {def}{=}}\ \varepsilon _{0}\mathbf {E} +\mathbf {P} }$；

其中，${\displaystyle \varepsilon _{0}}$是电常数，${\displaystyle \mathbf {P} }$是电极化强度。

所以，位移电流密度分为两个部分：

${\displaystyle \mathbf {J} _{D}=\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}+{\frac {\partial \mathbf {P} }{\partial t}}}$。

这方程式右手边的第一个项目是马克士威修正项目，在任何地方都可存在，甚至在真空也可以存在。马克士威修正项目并不涉及任何真实的电荷运动，但是，它描述一个含时电场的物理行为，就好像是真实的电流。第二个项目是电极化电流密度，与电介质内单独分子的极化性有关。

原本定律的延伸：马克士威-安培方程式

将马克士威修正项目加入安培方程式：

${\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {J} +\mu _{0}\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}}$  ;

或者，使用H场${\displaystyle \mathbf {H} }$和位移电流${\displaystyle \mathbf {D} }$来表达，

${\displaystyle \nabla \times \mathbf {H} =\mathbf {J} _{f}+{\frac {\partial \mathbf {D} }{\partial t}}}$。

这就是马克士威-安培方程式，可以补救原本安培环路定律的限制。

假若使用B场${\displaystyle \mathbf {B} }$的马克士威-安培方程式，由于习惯，时常会称${\displaystyle \varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}}$项目为位移电流密度。由于增添了位移电流，马克士威能够推论（正确地）光波是一种电磁波（请参阅电磁波条目）。

等价证明

马克士威-安培方程式的等价证明

这里证明方程式 ${\displaystyle \mathbf {\nabla } \times \mathbf {B} =\mu _{0}\mathbf {J} +\mu _{0}\epsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}}$。 等价于方程式 ${\displaystyle \nabla \times \mathbf {H} =\mathbf {J} _{f}+{\frac {\partial \mathbf {D} }{\partial t}}}$， 注意到只处理微分形式，而不处理积分形式。但这已足够了。因为，根据克耳文-斯托克斯定理，微分形式等价于积分形式。 回想电位移的定义式为 ${\displaystyle \mathbf {D} \ {\stackrel {def}{=}}\ \epsilon _{0}\mathbf {E} +\mathbf {P} }$。 还有，${\displaystyle \mathbf {H} }$的定义式为 ${\displaystyle \mathbf {H} \ {\stackrel {def}{=}}\ {\frac {1}{\mu _{0}}}\mathbf {B} -\mathbf {M} }$。 将这两个定义式代入H场${\displaystyle \mathbf {H} }$的马克士威-安培方程式， ${\displaystyle \nabla \times \left({\frac {1}{\mu _{0}}}\mathbf {B} -\mathbf {M} \right)=\mathbf {J} _{f}+\epsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}+{\frac {\partial \mathbf {P} }{\partial t}}}$。 经过一番运算，可以得到 ${\displaystyle \nabla \times \left({\frac {1}{\mu _{0}}}\mathbf {B} \right)=\mathbf {J} _{f}+\nabla \times \mathbf {M} +{\frac {\partial \mathbf {P} }{\partial t}}+\epsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}=\mathbf {J} _{f}+\mathbf {J} _{M}+\mathbf {J} _{P}+\epsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}}$。 稍加整理，即可得到磁场${\displaystyle \mathbf {B} }$的马克士威-安培方程式 ${\displaystyle \mathbf {\nabla } \times \mathbf {B} =\mu _{0}\mathbf {J} +\mu _{0}\epsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}}$。

CGS单位制的安培方程式

采用CGS单位制，安培方程式的积分形式，包括马克士威修正项目，可以写为

${\displaystyle \oint _{\mathbb {C} }\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}={\frac {1}{c}}\int _{S}\left(4\pi \mathbf {J} +{\frac {\partial \mathbf {E} }{\partial t}}\right)\cdot \mathrm {d} \mathbf {a} }$；

其中，${\displaystyle c}$是光速。

其微分形式可以写为

${\displaystyle \mathbf {\nabla } \times \mathbf {B} ={\frac {1}{c}}\left(4\pi \mathbf {J} +{\frac {\partial \mathbf {E} }{\partial t}}\right)}$。

备注

1. 在物理学上，英语 loop 和 circuit 在特殊语境下同义；在以下内文中，汉语对此术语 closed loop 的同义用词另有：环路、回路、回圈、环线、回线，或是闭环、闭路。

参见

• 电荷守恒定律

注释

1. 沿著闭合回路${\displaystyle \mathbb {C} }$线积分的方向有两种（顺时针方向及逆时针方向）。还有，${\displaystyle I\!\ }$是通过边缘为闭合回路${\displaystyle \mathbb {C} }$的曲面${\displaystyle \mathbb {S} }$的净自由电流，包括以某方向通过的电流，减去以相反方向通过的电流。但是，两种方向中，任何一种都可以选为正值。为了澄清这些模糊之处，必须使用右手定则：当右手食指朝著线积分方向指去时，伸直的大拇指会指向微小面元素向量，设定朝著这方向流动的电流为正值。
2. 通过边缘为闭合回路${\displaystyle \mathbb {C} }$的曲面有无限多选择（设想在一个闭合铁环上悬跨着一个肥皂泡，假若轻轻地往这个肥皂泡吹一口气，则泡沫的形状会变形）。不过选择哪一曲面都无所谓，因为任何边缘为${\displaystyle \mathbb {C} }$的曲面皆可被证明为正确的选择。

参考文献

1. 存档副本. [2022-04-21]. （原始内容存档于2022-04-21）.
2. David J Griffiths. Introduction to Electrodynamics 3rd Edition. Pearson/Addison-Wesley. 1999: 225, 321-325. ISBN 013805326X. 引文格式1维护：冗余文本 (link)
3. Daniel M. Siegel. Innovation in Maxwell's Electromagnetic Theory: Molecular Vortices, Displacement Current, and Light. Cambridge University Press. 2003: 96-98. ISBN 0521533295.
4. James C. Maxweel. On Physical Lines of Force (PDF). Philosophical Magazine and Journal of Science. 1961 [2009-08-08]. （原始内容存档 (PDF)于2009-06-12）.

外部链接

• Morgan, Kirby. 安培定律 (PDF). Project PHYSNET. [2009-08-08]. （原始内容 (PDF)存档于2006-02-21）. 外部链接存在于|publisher= (帮助)
• Smith, Walter Fox. 安培定律之歌 (PDF). PhysicsSongs.org. [2009-08-08]. （原始内容存档 (PDF)于2010-10-11）. 外部链接存在于|publisher= (帮助)