十七面体

在几何学中，十七面体是指有17个面的多面体，在十七面体当中没有任何一个形状是正多面体，换言之即正十七面体并不存在，但仍然有接近球形的十七面体，例如一些十七面体型的化学结构^[1][2]，但时其面并非由正多边形组成，虽然仍有许多由正多边形组成的十七面体，例如正五角罩帐和侧锥球状屋顶^[3]，但其对称性较低。此外，也存在非常多拓朴结构有明显差异的十七面体，例如十六角锥和十五角柱。

十七面体

部分的十七面体
	三侧锥六角柱
正五角罩帐	侧锥球状屋顶

工业上十七面体有许多用途，例如特殊设计的十七面体可以减少空隙方便堆放^[4][5]。

凸十七面体

在所有凸十七面体当中，拓朴结构有明显差异的凸十七面体，包含其镜射像共有6,415,851,530,241种凸十七面体有著至少11个顶点^[6]。两者具有不同的拓扑结构是代表他们面和顶点有不同的安排方式，使得其无法单靠扭曲或简单地通过改变边或面之间的长度或角度转换成另一种多面体的多面体。

此外由于无穷拉夫斯图的对称性是从三维空间的二十面体堆砌而来，因此具有凸十七面体的沃罗诺伊胞^[7]。

一些凸十七面体的例子比如八角锥柱^[8]、正五角罩帐、凸三侧锥六角柱、侧锥球状屋顶。

非凸十七面体

在几何学上也有许多非凸十七面体，像是星形柱体、锥体或台体，如五角锥五角星台^[9]。

常见的十七面体

十五角柱

十五角柱

十五角柱是一种底面为十五边形的柱体，是十七面体的一种，由17个面45条边和30个顶点组成。正十五角柱代表每个面都是正多边形的十五角柱，其每个顶点都是2个正方形和1个十五边形的公共顶点，顶点图以${\displaystyle 4{.}4{.}15}$表示，因此具有每个角等角的性质（点可递），可以归类为半正十七面体，不过他跟其他较接近球形的半正多面体相比之下变得比较扁一些。

正十五角柱在施莱夫利符号中可以用{15}×{}或t{2,15}来表示，在考克斯特符号（英语：Coxeter-Dynkin diagram）中可以用来表示，在威佐夫符号（英语：Wythoff symbol）中可以利用2 15 | 2来表示，在康威多面体表示法中可以利用P15来表示。底边长为${\displaystyle s}$、高为${\displaystyle h}$的正十五角柱体积${\displaystyle V}$和表面积${\displaystyle S}$为^[10]：

${\displaystyle V={\frac {15hs^{2}\cot {\frac {\pi }{15}}}{4}}\approx 17.6424hs^{2}}$

${\displaystyle S=15s\left(h+{\frac {s\cot {\frac {\pi }{15}}}{2}}\right)\approx 15s\left(h+2.35232s\right)}$

十六角锥

十六角锥

十六角锥是一种底面为十六边形的锥体，是十七面体的一种，具有17个面、32条边和17个顶点，其对偶多面体是自己本身。^[11]正十六角锥是指底面为正十六边形的十六角锥，在施莱夫利符号中可以用{}∨{16}来表示。底边长为${\displaystyle s}$、高为${\displaystyle h}$的正十六角锥体积${\displaystyle V}$和表面积${\displaystyle S}$为^[11]：

${\displaystyle V={\frac {4hs^{2}\cot {\frac {\pi }{16}}}{3}}\approx 6.70312hs^{2}}$

${\displaystyle S=4s\left({\sqrt {4h^{2}+s^{2}\cot ^{2}{\frac {\pi }{16}}}}+s\cot {\frac {\pi }{16}}\right)\approx 4s\left({\sqrt {4h^{2}+25.2741s^{2}}}+5.02734s\right)}$

八角锥柱

八角锥柱是指底面为八边形的角锥柱，由17个面、32条边和17个顶点组成，是一种十七面体。

五角罩帐

正五角罩帐

五角罩帐是以五边形为底的罩帐，是一种十七面体，由1个五边形顶面、1个十边形底面、6个五边形侧面和10个三角形侧面组成，共有15个面、35条边和20个顶点，其中五边形顶面与十边形底面互相平行，三角形侧面与五边形侧面交错地围绕轴分布在周围。

以正五边形为底的五角罩帐称为正五角罩帐。正五角罩帐可以顶面和侧面的五边形都为正五边形，此时的正五角罩帐所有面都是正多边形，是一种詹森多面体，也是唯一一个属于詹森多面体的罩帐^[12]。

正五角罩帐的对称群为C_5v（英语：Dihedral symmetry in three dimensions）群，阶数为10阶。

三角帐塔罩帐

三角帐塔罩帐是指底面为三角形的帐塔罩帐，由三角帐塔和三角罩帐以边数较多的底面互相贴合叠合而成，是一种十七面体。三角帐塔罩帐共有17个面、30条边和15个顶点所组成。在其17个面中，有2个三角形底面、9个三角形侧面、3个矩形侧面和3个五边形侧面。

三角帐塔罩帐依照三角帐塔和三角罩帐的贴合方式可以分成同相三角帐塔罩帐和异相三角帐塔罩帐。

同相三角帐塔罩帐

异相三角帐塔罩帐

十七面体列表

名称	种类	图像	符号	顶点	边	面	χ	面的种类	对称性	展开图
十五角柱	棱柱体		t{2,15} {15}x{}	30	45	17	2	2个十五边形 15个矩形	D15h, [15,2], (*15 2 2), order 60
十六角锥	棱锥体		( )∨{16}	17	32	17	2	1个十六边形 16个三角形	C16v, [16], (*16 16)
八角锥柱	角锥柱		P8+Y8	17	32	17	2	8个三角形 8个正方形 1个八边形	C8v, [8], (*88)
八角锥台锥	截角双锥			17	32	17	2	1个八边形 8个梯形 8个三角形	C8v, [8], (*88)
十五角锥台	锥台			30	45	17	2	2个十五边形 15个梯形	D15h, [15,2], (*15 2 2), order 60
五角罩帐	罩帐		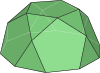	20	35	17	2	1个五边形顶面 1个十边形底面 5个五边形侧面 10个三角形侧面	C5v（英语：Dihedral symmetry in three dimensions）, [5], (*55), order 10
同相三角帐塔罩帐	帐塔罩帐			15	30	17	2	2个三角形底面 9个三角形侧面 3个矩形侧面 3个五边形侧面	C3v（英语：Dihedral symmetry in three dimensions）
异相三角帐塔罩帐

参考文献

1. V. Gold. Advances in Physical Organic Chemistry APL 第 14 卷. Academic Press. 1977: 227. ISBN 9780080581538.
2. Commonwealth Scientific and Industrial Research Organization (Australia), Institute of Physics (Great Britain). Australian Branch, Australian National Research Council, Australian Academy of Science. Australian Journal of Chemistry, 第 52 卷. Commonwealth Scientific and Industrial Research Organization. 1999: 343-822, 497.
3. Johnson, Norman W., Convex polyhedra with regular faces, Canadian Journal of Mathematics, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8
4. Pedrita, alongside Água de Luso. The bottle’s 17 faces. [2016-08-20]. （原始内容存档于2016-08-20）.
5. 以節省空間與堆疊的17面體瓶身設計. poloves. [2016-08-20]. （原始内容存档于2014-08-04）.
6. Counting polyhedra （页面存档备份，存于互联网档案馆） numericana.com [2016-1-10]
7. Schoen, Alan H., On the graph (10,3)-a (PDF), Notices of the American Mathematical Society, June–July 2008, 55 (6): 663 [2016-08-05], （原始内容存档 (PDF)于2016-09-28）.
8. Heptakaidecahedra (polyhedra with 17 faces). korthalsaltes.com. [2016-08-05]. （原始内容存档于2016-10-13）.
9. Paper Pentagonal-pentagrammic Shape. korthalsaltes.com. [2016-08-05]. （原始内容存档于2016-10-13）.
10. Wolfram, Stephen. "pentadecagonal prism". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英语）.
11. Wolfram, Stephen. "hexadecagonal pyramid". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英语）.
12. Johnson, Norman W.（英语：Norman Johnson (mathematician)）, Convex polyhedra with regular faces, Canadian Journal of Mathematics（英语：Canadian Journal of Mathematics）, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8.