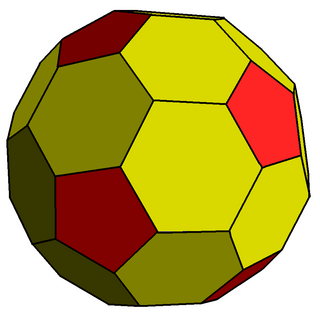
在几何学中，倒角十二面体是一种凸多面体，由12个五边形和30个六边形组成，那30个六边形是全等的，惟非正六边形。倒角十二面体共有42个面、120个边和80个顶点，是五角化截半二十面体的对偶多面体。
是由正十二面体经由倒角变换产生的多面体，即是将正十二面体中的30条边以六边形取代所形成的凸多面体，因此倒角二十面体共有30个六边形，而原本的五边形被保留，但倒角变换产生的六边形非正边形。
等价的多面体
交错截角菱形三十面体与倒角十二面体是相同的多面体，但是构成方式不太相同。交错截角菱形三十面体是经过交错截角变换构成的，即将其顶点不全部截掉，而是交错截去，康威符号计为h，对于菱形三十面体会造成两种结果：仅切去有五个相邻面的顶点以及仅切去有三个相邻面的顶点，而仅有切去相邻五个面的顶点的多面体与倒角二十面体等价，因此若称为交错截角菱形三十面体存在歧意：可能为倒角二十面体或倒角十二面体。
交错截角菱形三十面体就是切去顶点的菱形三十面体，但是只能切去五个相邻面的顶点。这12个五阶顶点（有五个相邻面的顶点）可以被截成等长的，这使得原来的菱形面变成非正六边形，截去的顶点成为正五边形。它在顶点配置为6.6.6的两面角是arccos(-1/sqrt(5)) = 116.565度，另一个在5.6.6的两面角近似值为121.717 度。
相关多面体
参考文献
- Deza, A.; Deza, M.; Grishukhin, V., Fullerenes and coordination polyhedra versus half-cube embeddings, Discrete Mathematics, 1998, 192 (1): 41–80 [2013-03-19], doi:10.1016/S0012-365X(98)00065-X, （原始内容存档于2007-02-06）.
- VTML polyhedral generator（页面存档备份，存于互联网档案馆） Try "t5daD" (康威多面体表示法)
- Zometool model
- Fullerene C80
Wikiwand - on
Seamless Wikipedia browsing. On steroids.