数值分析里的中点法(midpoint method)是求解常微分方程的一种数值方法,属于单步法。

 中点法的图示说明,假设
中点法的图示说明,假设 等于
等于 的实际值。中点法计算
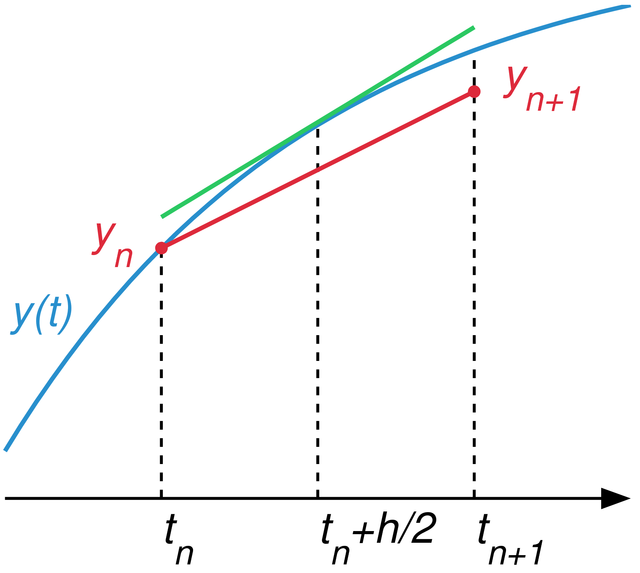
的实际值。中点法计算 让红色的弦近似平行于中点处的切线(绿色)
让红色的弦近似平行于中点处的切线(绿色)
上式的显式中点法为
 | | 1e |
隐式中点法为
 | | 1i |
 。此处
。此处 是步阶长度,是一个小的正数,
是步阶长度,是一个小的正数, ,而
,而 是计算
是计算 的近似值。显式中点法也称为是改良的欧拉方法(modified Euler method)[1],隐式中点式是最简单的配置法(Collocation method),可用在哈密顿力学,也就是辛积分器。
的近似值。显式中点法也称为是改良的欧拉方法(modified Euler method)[1],隐式中点式是最简单的配置法(Collocation method),可用在哈密顿力学,也就是辛积分器。
此方法的名称是因为上述公式会用到函数在 位置的值,也就是在
位置的值,也就是在 以及
以及 中点时的值,前者的值已知,后者的值未知,在计算中点的值时,也需要有一些假设,才能进行计算。
中点时的值,前者的值已知,后者的值未知,在计算中点的值时,也需要有一些假设,才能进行计算。
配合图示(见右图)会比较容易理解此一方法。在原始的欧拉方法里,会用 ,计算曲线在
,计算曲线在 处的切线。此切线和垂直线
处的切线。此切线和垂直线 的交点即为下一个点
的交点即为下一个点 的值。不过,若此函数的二阶导数在时间
的值。不过,若此函数的二阶导数在时间 和
和 的区间均为正, 或是均为负(如图中的例子),随著
的区间均为正, 或是均为负(如图中的例子),随著 加大,曲线和切线的距离会越来越远,导致大误差。图中所画的中点的切线(上方,绿线)比较可以近似这段曲线。不过因为要求解的就是此一曲线,时间
加大,曲线和切线的距离会越来越远,导致大误差。图中所画的中点的切线(上方,绿线)比较可以近似这段曲线。不过因为要求解的就是此一曲线,时间 的资讯已知,其他资讯不足,可能无法精准的画出中点处的切线。
的资讯已知,其他资讯不足,可能无法精准的画出中点处的切线。
因此,会先用原始的欧拉方法估计在中点的 值,再用
值,再用 以及估计的中点资讯,计算切线斜率。用改善后的切线从
以及估计的中点资讯,计算切线斜率。用改善后的切线从 计算
计算 的值。最后一步即为图的红色弦线。因为红色弦线是估计值,用的是
的值。最后一步即为图的红色弦线。因为红色弦线是估计值,用的是 在中点处的估计值,不一定真的会和绿线(真正的中点切线)平行,仍会有误差。
在中点处的估计值,不一定真的会和绿线(真正的中点切线)平行,仍会有误差。
中点法每一步的局部误差是 ,全域误差是
,全域误差是 。其运算比欧拉方法要大,但在
。其运算比欧拉方法要大,但在 的过程中,中点法的误差会比欧拉方法降低的更快。
的过程中,中点法的误差会比欧拉方法降低的更快。
此法也是高阶方法(如龙格-库塔法)的范例之一。










































