ΛCDM模型

ΛCDM模型（英语：ΛCDM Model）是所谓Λ-冷暗物质（Lambda Cold Dark Matter）模型的简称。它在大爆炸宇宙学中经常被称作索引模型，这是因为它尝试解释了对宇宙微波背景辐射、宇宙大尺度结构以及宇宙加速膨胀的超新星观测。它是当前能够对这些现象提供融洽合理解释的最简单模型。

• Λ意为宇宙学常数，是解释当前宇宙观测到的加速膨胀的暗能量项。宇宙学常数经常用${\displaystyle \Omega _{\Lambda }\,}$表示，含义是当前宇宙中暗能量相对于一个平直时空的宇宙的能量所占的比例。最近对${\displaystyle \Omega _{\Lambda }\,}$的观测结果包括暗能量巡天测得的66.9%^[1]，以及2018年普朗克卫星通过微波背景辐射测得比例约为68.3%。^[2]
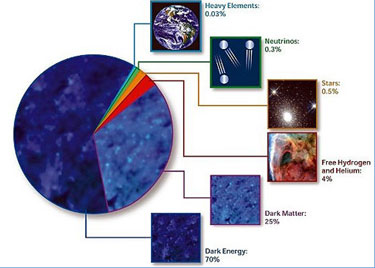
• 冷暗物质是一种暗物质模型，即它认为在宇宙早期辐射与物质的能量分布相当时暗物质的速度是非相对论性的（远小于光速），因此暗物质是冷的；同时它们是非重子构成的；不会发生碰撞（指暗物质的粒子不会与其他物质粒子发生引力以外的基本相互作用）或能量损耗（指暗物质不会以光子的形式辐射能量）的。冷暗物质占了当前宇宙能量密度的26.5%。^[3]剩余的4.9%的包括宇宙中所有的由重子（以及光子等规范玻色子）构成的物质：行星、恒星以及气体星云等。^[4]
• 模型假设了具有接近尺度不变的能量谱的太初微扰，以及一个空间曲率为零的宇宙。它同时假设了宇宙没有可观测的拓扑，从而宇宙实际要比可观测的粒子视界要大很多。这些都是宇宙暴胀理论的预言。
• 模型采用了弗里德曼-勒梅特-罗伯逊-沃尔克度规、弗里德曼方程和宇宙的状态方程来描述从暴胀时期之后至今以及未来的宇宙。

一张表示宇宙间不同物质能量成分的饼图，大约有96%的能量来自奇异的暗物质和暗能量。

ΛCDM模型，加速扩张的宇宙。

在宇宙学中，这些是能够构建一个自洽的物理宇宙模型的最简单的假设。而ΛCDM模型终归只是一个模型，宇宙学家们预计在对相关的基础物理了解更多之后，这些简单的假设都有可能被证明并不完全准确。具体而言，暴胀理论预言宇宙的空间曲率在10^-5到10^-4的量级。另外也很难相信暗物质的温度是绝对零度。ΛCDM模型也并没有在基础物理层面上解释暗物质、暗能量以及具有接近尺度不变的能量谱的太初微扰的起源：从这个意义上说，它仅仅是一个有用的参数化形式。

参数

模型含有六个基本参数。

• 哈勃常数——决定宇宙的膨胀速率，以及宇宙闭合所需的临界密度${\displaystyle \rho _{0}\,}$。
• 重子的密度、暗物质的密度和暗能量的密度，它们都归一到临界密度，即如${\displaystyle \Omega _{b}=\rho _{b}/\rho _{0}\,}$。由于模型假设空间是平直的，三者的密度之和等于临界密度，从而暗能量的密度并不是一个独立参数。
• 光深度——决定宇宙再电离的红移。
• 密度涨落的信息由太初微扰的涨落振幅（源自宇宙暴胀）和能谱指数共同决定，其中能谱指数${\displaystyle n_{s}\,}$表征涨落如何随尺度变化（${\displaystyle n_{s}=1\,}$表示尺度不变的能谱）。

模型中包含的误差分析显示，实际的真实值有68%的置信概率落到测量结果的上下限之间。误差并不是非高斯分布的，它们是通过对威尔金森微波各向异性探测器的数据以蒙特卡罗马尔可夫链方法进行误差分析得出的，其中也使用了斯隆数字巡天和Ia型超新星的观测数据。

参数	数值	描述
基本参数
Ωb	${\displaystyle 0.0486_{-0.0010}^{+0.0010}}$	重子密度
Ωc	${\displaystyle 0.2589_{-0.0057}^{+0.0057}}$	暗物质密度
t0	${\displaystyle 13.799_{-0.021}^{+0.021}\times 10^{9}}$y	宇宙的年龄
ns	${\displaystyle 0.9667_{-0.0040}^{+0.0040}}$	尺度能谱指数
${\displaystyle \Delta _{R}^{2}}$	${\displaystyle 2.441_{-0.092}^{+0.088}\times 10^{-9}}$	尺度涨落振幅， k0 = 0.002 Mpc-1
τ	${\displaystyle 0.066_{-0.012}^{+0.012}}$	宇宙再电离所需的光深度
固定参数
Ωtot	${\displaystyle 1}$	空间曲率
w	${\displaystyle -1}$	状态方程
r	${\displaystyle 0}$	张量标量比
d ns / d ln k	${\displaystyle 0}$	能谱指数的变化
Σmν	${\displaystyle 0.06}$ eV/c2	中微子质量总和
Neff	${\displaystyle 3.046}$	有效的自由相对论度数
导出参数
H0	${\displaystyle 67.74_{-0.46}^{+0.46}}$ km s-1 Mpc-1	哈勃常数
Ωm	${\displaystyle 0.3089_{-0.0062}^{+0.0062}}$	总物质密度（重子+暗物质）
ΩΛ	${\displaystyle 0.6911_{-0.0062}^{+0.0062}}$	暗能量密度
ρcrit	${\displaystyle 8.62_{-0.12}^{+0.12}\times 10^{-27}}$ kg/m3	临界密度
σ8	${\displaystyle 0.8159_{-0.0086}^{+0.0086}}$	星系涨落指数 在平均8h-1 Mpc半径的球形上
zre	${\displaystyle 8.5_{-1.1}^{+1.0}}$	再电离红移

ΛCDM模型的优势

在所有宇宙学模型中，ΛCDM模型取得了最显著的成功；它以卓越的精确度描述了涵盖几乎所有领域的天文观测结果。^[5]​其主要成功之处包括：

• 精确拟合普朗克卫星和阿塔卡马宇宙学望远镜观测到的宇宙微波背景辐射角功率谱。^[2][6]
• 准确描述由于最后散射面波动引起的CMB辐射的线性E模偏振。^[7]
• 准确预测由原初引力波引起的CMB辐射的B模式偏振。^[8]
• 观测到来自128亿光年外星系的H₂O发射谱，与由比我们当前观测到的3K CMB更高能量（16-20K）的宇宙背景辐射激发的分子相一致。^[9]
• 准确预测了由大爆炸核合成产生的氘的原初丰度。^[10]

除了成功解释2000年前的多项观测外，该模型还做出了多项成功预测：​

• 成功预测了重子声学振荡特征，并于2005年由SDSS和2dFGRS研究组发现；^[11]
• 成功预测了2000年首次观测到的弱引力透镜统计特性；
• 成功预测了2002年由DASI发现的CMB偏振特性。

在2015年普朗克数据发布中，温度（TT）功率谱中观测到七个峰值，温度-偏振（TE）交叉谱中六个峰值，以及偏振（EE）谱中五个峰值。​仅通过TT谱就能很好地约束六个自由参数，然后TE和EE谱可以在没有进一步调整的情况下，由ΛCDM模型以百分之几的精度进行理论预测。

扩展模型

由最简单的ΛCDM模型可以进一步扩展为其他模型，例如可以用第五元素替代宇宙常数项，在这种情况下暗能量的状态方程可以为-1以外的其他值。宇宙暴胀预言了时空度规张量的涨落（即引力波），它们的振幅可由张量标量比（tensor-to-scalar ratio）参数化，而后者由暴胀的能量尺度决定。其他对模型的修正包括允许空间曲率的存在或随时间变化的能谱指数，这些在一般观点看来都是和暴胀理论相违背的。

允许引入这些参数通常都会增加上述基本参数的测量误差，并在某种程度上使测量值产生偏移。

参数	数值	描述
${\displaystyle \Omega _{tot}}$	${\displaystyle 1.0023_{-0.0054}^{+0.0056}}$	空间曲率
${\displaystyle w}$	${\displaystyle -0.980_{-0.053}^{+0.053}}$	状态方程
${\displaystyle r}$	${\displaystyle <0.11}$, k0 = 0.002 Mpc-1 (2σ)	张量标量比
${\displaystyle d\ n_{s}/d\ \ln k}$	${\displaystyle -0.022_{-0.020}^{+0.020}}$, k0 = 0.002 Mpc-1	能谱指数的变化
${\displaystyle \Sigma m_{\nu }}$	${\displaystyle <0.58}$ eV/c2 (2σ)	中微子质量总和
${\displaystyle \Omega _{v}h^{2}}$	${\displaystyle <0.0062}$	物理中微子密度参数

这些参数与一个具有参数${\displaystyle \omega =-1\,}$的宇宙的状态方程、以及一个空间曲率为零的情形相洽。