“
品质因数 ”重定向至此。关于Figure of merit的中文条目,请见“
品质因数 (性能) ”。
品质因子 或Q因子 是物理 及工程 中的无因次 参数,是表示振子 阻尼 性质的物理量[ 1] 共振频率 相对于频宽 的大小[ 2] 单摆 在空气中运动,其Q因子较高,而在油中运动的单摆Q因子较低。高Q因子的振子一般其阻尼也较小。
一阻尼谐振子的频宽 ,
Δ
f
{\displaystyle \Delta f}
f
0
/
Δ
f
{\displaystyle f_{0}/\Delta f}
Q因子较高的振子在共振 时,在共振频率附近的振幅较大,但会产生的共振的频率范围比较小,此频率范围可以称为频宽 。例如一台无线电接收器内的调谐电路 Q因子较高,要调整接收器对准一特定频率会比较困难,但其选择性
系统的Q因子可能会随著应用场合及需求的不同而有大幅的差异。强调阻尼特性的系统(例如防止门突然关闭的阻尼器)其Q因子为1 ⁄2 音叉 的Q因子大约为1000,原子钟 、加速器中的超导射频 光学共振腔 的Q因子可以到1011 [ 3] [ 4]
Q因子的概念是来自电子工程中,评量一调谐电路或其他振子的“品质”。
Q因子可定义为在一系统的共振频率 下,当信号振幅 不随时间变化时,系统储存能量和每个周期外界所提供能量的比例(此时系统储存能量也不随时间变化):
Q
=
2
π
×
Energy Stored
Energy dissipated per cycle
=
2
π
f
r
×
Energy Stored
Power Loss
.
{\displaystyle Q=2\pi \times {\frac {\mbox{Energy Stored}}{\mbox{Energy dissipated per cycle}}}=2\pi f_{r}\times {\frac {\mbox{Energy Stored}}{\mbox{Power Loss}}}.\,}
大部份的共振系统都可以用二阶的微分方程表示,Q因子中2π 的系数,使Q因子可以表示成只和二阶微分方程系数有关的较简单型式。在电机系统中,能量会储存在理想无损失的电感 及电容 中,损失的能量则是每个周期由电阻损失能量的总和。力学系统储存的能量是该时间动能 及位能 的和,损失的能量则是因为摩擦力或阻力所消耗的能量。
针对高Q因子的系统,也可以用下式计算的Q因子,在数学上也是准确的:
Q
=
f
r
Δ
f
=
ω
r
Δ
ω
,
{\displaystyle Q={\frac {f_{r}}{\Delta f}}={\frac {\omega _{r}}{\Delta \omega }},\,}
其中fr 为共振频率,Δf 为频宽,ωr = 2πfr 是以角频率 表示的共振频率,Δω 是以角频率 表示的频宽
在像电感等储能元件的规格中,会用到和频率有关的Q因子,其定义如下[ 5]
Q
(
ω
)
=
ω
×
Maximum Energy Stored
Power Loss
,
{\displaystyle Q(\omega )=\omega \times {\frac {\mbox{Maximum Energy Stored}}{\mbox{Power Loss}}},\,}
其中ω 是计算储存能量和功率损失时的角频率。若电路中只有一个储能元件(电感或是电容),也可用上式来定义Q因子,此时Q因子会等于无功功率 相对有功功率 的比例。
Q因子可决定一个简单阻尼谐振子 的量化特性(有关数学的细节及不同系统的行为,请参考谐振子 及线性时不变系统理论 等条目)。
低Q因子的系统(Q < ½)是过阻尼系统。过阻尼系统不会振荡,当偏离稳态输出平衡点时,会以指数衰减 的方式,渐近式的回到稳态输出。其冲激响应 是二个不同速度的指数衰减函数的和。当Q因子减少时,衰减较慢的响应函数其影响会变明显,因此整个系统会变慢。一个Q因子很低的二阶系统其步阶响应 类似一阶系统。 高Q因子的系统(Q > ½)是欠阻尼系统。欠阻尼系统在特定频率的输入下,其输出会振荡,其振幅也会指数衰减。Q因子略高于½的系统可能会振荡一或二次。若Q因子提高,阻尼的效果也会降低。高品质的钟在敲击后可以长时间发出单一音调的声音,没有阻尼的谐振系统其Q因子是无限大,类似一个敲击后可永远发出声音的钟。若二阶低通滤波器 有很高的Q因子,其步阶响应一开始会快速上升,在平衡点附近震荡,最后才收敛到稳态的值。 Q因子为½的系统是临界阻尼系统。临界阻尼系统和过阻尼系统一様不会震荡,也不会有过冲 的情形。临界阻尼系统和欠阻尼系统一様,会对阶跃 有快速的响应,临界阻尼可以使系统在不过冲的条件下有最快的反应,实际的系统若要求更快的反应,一般会允许一定程度的过冲,若系统不允许过冲,可能会使反应时间放慢,以提供一定的安全系数 。 在负回授 系统中,闭回路系统的响应常常用二阶系统来表示。设定开回路系统的相位裕度 可以决定闭回路系统的Q因子,当相位裕度减少时,对应的二阶闭回路系统振荡会变大,也就是Q因子提高。
单位增益的Sallen–Key拓扑结构
1
/
2
{\displaystyle 1/2}
[来源请求]
巴特沃斯滤波器 (有最平坦通带频率响应的的连续时间滤波器)为欠阻尼系统,Q因子为
1
/
2
{\displaystyle 1/{\sqrt {2}}}
[ 6] 贝塞尔滤波器 (有最平坦群延迟 的连续时间滤波器)为欠阻尼系统,Q因子为
1
/
3
{\displaystyle 1/{\sqrt {3}}}
[来源请求]
根据物理学,Q因子等于
2
π
{\displaystyle 2\pi }
[ 7]
Q因子是无因次的参数,是比较系统振幅衰减的时间常数 和振荡周期后的结果。当Q因子数值较大时,Q因子可近似为系统从开始振荡起,一直到其能量剩下原来的
1
/
e
2
π
{\displaystyle 1/e^{2\pi }}
[ 8]
共振的频宽可以用下式表示
Δ
f
=
f
0
Q
{\displaystyle \Delta f={\frac {f_{0}}{Q}}\,}
其中
f
0
{\displaystyle f_{0}}
共振频率 ,
Δ
f
{\displaystyle \Delta f}
频宽 ,也就是能量超过峰值能量一半以上的频率范围。
Q因子、阻尼比 ζ及衰减率 α之间有以下的关系[ 9]
ζ
=
1
2
Q
=
α
ω
0
.
{\displaystyle \zeta ={\frac {1}{2Q}}={\alpha \over \omega _{0}}.}
因此Q因子可表示为
Q
=
1
2
ζ
=
ω
0
2
α
,
{\displaystyle Q={\frac {1}{2\zeta }}={\omega _{0} \over 2\alpha },}
而指数衰减率可表示为
α
=
ζ
ω
0
=
ω
0
2
Q
.
{\displaystyle \alpha =\zeta \omega _{0}={\omega _{0} \over 2Q}.}
二阶低通滤波器的响应函数可以用下式来表示[ 9]
H
(
s
)
=
ω
0
2
s
2
+
ω
0
Q
⏟
2
ζ
ω
0
=
2
α
s
+
ω
0
2
{\displaystyle H(s)={\frac {\omega _{0}^{2}}{s^{2}+\underbrace {\frac {\omega _{0}}{Q}} _{2\zeta \omega _{0}=2\alpha }s+\omega _{0}^{2}}}\,}
若此系统的
Q
>
0.5
{\displaystyle Q>0.5}
共轭复数 极点,其实部 为
α
{\displaystyle \alpha }
α
{\displaystyle \alpha }
冲激响应 指数衰减 的速率。Q因子大表示其衰减率较慢,因此Q因子很大的系统可以持续振荡较长的时间。例如高Q因子的钟,用锤子敲击后,其输出近似纯音 ,且可以维持很长的时间。
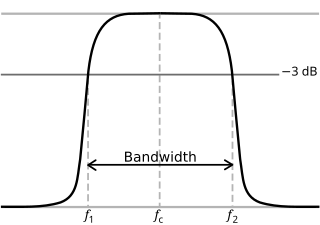
滤波器振幅增益的图,其中标示频宽为增益值为-3 dB的宽度,增益约为0.707倍,能量是峰值的一半。图中的频率轴可以是线性尺度或是对数尺度。 对电子共振系统而言,Q因子表示电阻 的影响,若针对机电共振系统(例如石英晶体谐振器 ),也包括摩擦力 的影响。
理想串联RLC电路 的Q因子为:[ 10]
Q
=
1
R
L
C
=
ω
0
L
R
=
1
ω
0
R
C
{\displaystyle Q={\frac {1}{R}}{\sqrt {\frac {L}{C}}}={\frac {\omega _{0}L}{R}}={\frac {1}{\omega _{0}RC}}}
其中
R
{\displaystyle R}
L
{\displaystyle L}
C
{\displaystyle C}
电阻 、电感 和电容 ,若电阻值越大,Q因子越小。
并联RLC电路的Q因子恰为对应串联电路Q因子的倒数:[ 11]
Q
=
R
C
L
=
R
ω
0
L
=
ω
0
R
C
{\displaystyle Q=R{\sqrt {\frac {C}{L}}}={\frac {R}{\omega _{0}L}}=\omega _{0}RC}
若将电阻、电感和电容并联形成一电路,并联电阻值越小,其阻尼的效果越大,因此Q因子越小。
若是电感和电容并联的电路,而主要损失是电感内,和电感串联的电阻R,其Q因子和串联RLC电路相同,此时降低寄生电阻R可以提升Q因子,也使频宽缩小到需要的范围内。
对于一个有阻尼的质量-弹簧系统,可以用Q因子表示简化的黏滞 阻尼或阻力对系统的影响,其中的阻尼力(或阻力)和速度成正比。此系统的Q因子可以用下式表示:
Q
=
M
k
D
,
{\displaystyle Q={\frac {\sqrt {Mk}}{D}},\,}
其中M是质量,k是弹簧常数 ,而D是阻力系数,可用下式来定义:
F
damping
=
−
D
v
{\displaystyle F_{\text{damping}}=-Dv}
其中
F
damping
{\displaystyle F_{\text{damping}}}
v
{\displaystyle v}
[ 13]
存档副本 (PDF) . [2012-03-31 ] . (原始内容存档 (PDF) 于2013-07-31).Jackson, R. Novel Sensors and Sensing. Bristol: Institute of Physics Pub. 2004: 28. ISBN 0-7503-0989-X Benjamin Crowell. Vibrations and Waves . Light and Matter online text series. 2006 [2012-04-03 ] . (原始内容存档 于2011-04-08). , Ch.2William McC. Siebert. Circuits, Signals, and Systems. MIT Press.
存档副本 . [2012-04-02 ] . (原始内容存档 于2012-01-10).存档副本 (PDF) . [2012-04-03 ] . (原始内容存档 (PDF) 于2020-11-25).