四角锥柱

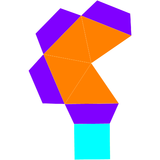
在几何学中，四角锥柱是底面为四边形的角锥柱，其可以视为将底面全等的四角锥与四角柱叠合所形成的立体，又称为方尖碑（Obelisk）^[1]。若底面为正方形则称为正四角锥柱，等边的正四角锥柱是一种詹森多面体^[1]。四角锥柱具有9个面、16个边、和9个顶点，每个四角锥柱皆为一个九面体。

正四角锥柱

类别	棱锥柱 詹森多面体 J7 - J8 - J9
对偶多面体	四角锥柱（自身对偶）
识别
鲍尔斯缩写 （verse-and-dimensions的wikia：Bowers acronym）	esquipy
数学表示法
康威表示法	P4+Y4
性质
面	9
边	16
顶点	9
欧拉特征数	F=9, E=16, V=9 （χ=2）
组成与布局
面的种类	4个三角形 5个正方形
顶点布局 （英语：Vertex_configuration）	4个(43) 1个(34) 4个(32.42)
对称性
对称群	C4v（英语：cyclic symmetries）, [4], (*44)
旋转对称群 （英语：Rotation_groups）	C4, [4]+, (44)
特性
凸、demi-regular
图像
四角锥柱（自身对偶） （对偶多面体） （展开图）
查 论 编

詹森多面体

考虑一个正四角锥柱，若每一个面皆为正多边形，则为92种Johnson多面体（J₈）中的其中一个，也是角锥柱的一种，可由詹森多面体中的正四角锥与柏拉图立体中的立方体于相等大小的正方形面接合而组成，这种立体又称为侧锥立方体（augmented cube）^[2]。詹森多面体是凸多面体，面皆由正多边形组成但不属于均匀多面体，共有92种。这些立体最早在1966年由诺曼·詹森（英语：Norman Johnson (mathematician)）（Norman Johnson）命名并给予描述^[3]。

性质

正四角锥柱共由9个面、16条边、和9个顶点组成^[4][5][2][6]。在其9个面中，有4个正三角形面和5个正方形面^[4]。在其9个顶点中，有3种顶点，分别是4个三角形的公共顶点，在顶点图中可以用[3⁴]来表示^[7]，这种顶点有1个^[2]、另一种顶点为2个三角形和2个正方形的公共顶点，在顶点图中可以用[3²,4²]来表示^[7]，这种顶点有4个^[2]、还有一种顶点是3个正方形的公共顶点，在顶点图中可以用[4³]来表示^[7]，这种顶点有4个^[2]。

体积与表面积

若一个正四角锥柱边长为${\displaystyle L}$，则其体积${\displaystyle V}$与表面积${\displaystyle A}$为：^[8]

${\displaystyle V=L^{3}\left(1+{\frac {\sqrt {2}}{6}}\right)\approx L^{3}\cdot 1.23570226}$

${\displaystyle A=L^{2}\cdot \left(5+{\sqrt {3}}\right)\approx L^{2}\cdot 6.732050808}$

这样的正四角锥柱整体的高${\displaystyle H}$为：

${\displaystyle H=L\cdot \left(1+{\frac {\sqrt {2}}{2}}\right)\approx L\cdot 1.707106781}$

二面角

正四角锥柱共有3种二面角，分别为三角形和正方形的二面角、三角形和三方形的二面角以及正方形和正方形的二面角^[7]。其中正方形和正方形的二面角为直角，即90度角。^[7]

${\displaystyle \angle }$正方形${\displaystyle ,}$正方形${\displaystyle \,=90^{\circ }}$

而三角形和正方形的二面角为负根号三分之二的反馀弦值，约为144.7356度：^[7]

${\displaystyle \angle }$三角形${\displaystyle ,}$正方形${\displaystyle \,=\arccos \left(-{\sqrt {\frac {2}{3}}}\right)\approx 2.52611294\approx 144.735610^{\circ }}$

三角形和三方形的二面角为负三分之一的反馀弦值，约为109.471度：^[7]

${\displaystyle \angle }$三角形${\displaystyle ,}$三方形${\displaystyle \,=\arccos \left(-{\frac {1}{3}}\right)\approx 1.9106332\approx 109.471221^{\circ }}$

顶点座标

若一个正四角锥柱边长为单位长，则其顶点座标为：^[9]

${\displaystyle \left(\pm {\frac {1}{2}},\,\pm {\frac {1}{2}},\,\pm {\frac {1}{2}}\right)}$

${\displaystyle \left(0,\,0,\,{\frac {1+{\sqrt {2}}}{2}}\right)}$

对偶多面体

四角锥柱的对偶多面体为四角锥台锥，由4个三角形、1个正方形和4个梯形组成。

四角锥柱的对偶多面体	对偶多面体的展开图

相关多面体

四角锥柱是以四边形为底的角锥柱。^[1]以其他多边形为底的角锥柱有：

棱锥柱体

二角锥柱	三角锥柱	四角锥柱	五角锥柱	六角锥柱	七角锥柱	...	圆锥柱

四角锥柱可以视为侧锥四角柱，其为底面为四边形之柱体对应的侧锥柱体，其他的侧锥柱体有：

侧锥柱体

3	4	5	6	7
侧锥三角柱	侧锥四角柱	侧锥五角柱	侧锥六角柱	侧锥七角柱

此外，正四角锥柱可以与正四面体共同填满空间^[10]。

参见

• 詹森多面体
• 正方体
• 正四角锥

参考文献

1. Weisstein, Eric W. (编). Elongated Square Pyramid. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
2. Elongated square pyramid. polyhedra.tessera.li. [2022-09-07]. （原始内容存档于2022-09-07）.
3. Johnson, Norman W., Convex polyhedra with regular faces, Canadian Journal of Mathematics（英语：Canadian Journal of Mathematics）, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8
4. David I. McCooey. Johnson Solids: Elongated Square Pyramid. [2022-09-07]. （原始内容存档于2022-09-07）.
5. The Elongated Square Pyramid. qfbox.info. [2022-09-07]. （原始内容存档于2022-10-05）.
6. V. Bulatov. elongated square pyramid. [2022-09-07]. （原始内容存档于2022-05-22）.
7. Richard Klitzing. elongated square pyramid, esquipy. bendwavy.org. [2022-09-07]. （原始内容存档于2022-11-14）.
8. Sapiña, R. Area and volume of the Johnson solid J₈. Problemas y Ecuaciones. [2020-08-28]. ISSN 2659-9899. （原始内容存档于2020-09-30） （西班牙语）.
9. David I. McCooey. Data of Elongated Square Pyramid. [2022-09-07]. （原始内容存档于2022-09-07）.
10. J8 honeycomb. woodenpolyhedra.web.fc2.com. [2022-09-07]. （原始内容存档于2022-08-07）.