双四角锥

在几何学中，双四角锥是指以四边形做为基底的双锥体，由于双锥体是由二个锥体叠起来的，因此不存在底面，因此只能讨论其基底之形状。当基底的形状为正方形时会成为双正四角锥又称为正四角双锥。若基底的形状为正方形且每个面皆为正三角形则为正八面体。所有四角柱都有8个面6个顶点和12个边。对偶多面体是四角柱。

只要基底是四边形皆称为双四角锥

双四角锥

类别	双锥体
对偶多面体	四角柱
数学表示法
考克斯特符号 （英语：Coxeter-Dynkin diagram）
施莱夫利符号	{ }+{4}
康威表示法	dP4
性质
面	8
边	12
顶点	6
欧拉特征数	F=8, E=12, V=6 （χ=2）
组成与布局
面的种类	8个三角形（侧面） 基底为四边形
面的布局 （英语：Face configuration）	V4.4.4
对称性
对称群	D4h, [4,2], (*224), order 16
旋转对称群 （英语：Rotation_groups）	D4, [4,2]+, (224), order 8
特性
凸
图像
四角柱 （对偶多面体）

正四角双锥

主条目：正八面体

基底为正方形和且每一个面皆为正三角形的双锥体称为正四角双锥，即是正八面体，是帕雷托立体之一。

正四角双锥

长方双锥

基底为长方形的双四角锥称为长方双锥。

长方双锥

梯形双锥

基底是梯形的双四角锥称为梯形双锥

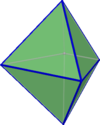梯形双锥

凹双四角锥

底面为凹筝形的双四角锥

凹双四角锥是指有一个角大于180度的双四角锥，通常凹双四角锥都是因为基底为凹四边形才会构成

相关多面体与镶嵌

半正方形二面体球面多面体

对称群（英语：List of spherical symmetry groups）：[4,2], (*422)							[4,2]+, (422)	[1+,4,2], (222)	[4,2+], (2*2)
{4,2}	t{4,2}	r{4,2}	2t{4,2}=t{2,4}	2r{4,2}={2,4}	rr{4,2}	tr{4,2}	sr{4,2}	h{4,2}	s{2,4}
半正对偶
V42	V82	V42	V4.4.4	V24	V4.4.4	V4.4.8	V3.3.3.4	V22	V3.3.2.3

半正对偶双棱锥

2	3	4	5	6	7	8	9	10	11	12	...	∞
作为球面镶嵌

参见