Loading AI tools
来自维基百科,自由的百科全书
罗宾森投影法(Robinson projection)是1960年代以来广泛使用的一种地图投影方法,这种投影方法可以同时在地图上展示整个世界。这种方法试图寻找一种在平面图上显示整个地球的方便的折衷方案。
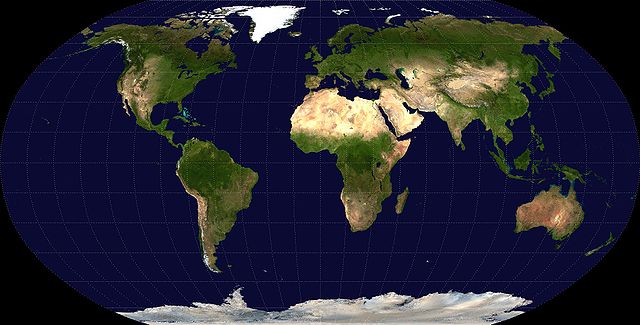
罗宾森投影1963年由亚瑟·H·罗宾森博士开发。使用了笔直的纬线,且每根经线之间的空间均匀分布,罗宾森投影被列为伪圆柱投影的一种。中间的经线也是直线,而其它经线则为曲线。罗宾森规定了这一投影方法在对经纬度进行特定插值后参考直角坐标系的数值表进行构建。中间的位置通过插值后得到,可以参见下方的表格。这一方法也反映了在研究这一投影方法的过程中,他做了一系列的试验和插值直至确定了最适合的经线形状和纬线的间距。相比之下,多数其它投影方法只是一些数学方程。罗宾森投影也出现了很多方程的表示法,以取代查找表格的方法。
罗宾森1946年起是威斯康星大学麦迪逊分校地理系的教授,并于1980年退休。由于兰德麦奈利出版社不满意现有对整个世界进行直观描述的现有投影方法,便委托罗宾森教授开发了这一投影方法。兰德麦奈利出版社从此在很多地图集和书中大量使用这一方法。这是第一个大型私有企业委托完成的重要地图投影方法。[1]这一投影方法最初被罗宾森命名为“矫形法(orthophanic)”(意为“正确的样子”),但这个名称从来没有被使用,并很快就变成了著名的罗宾森投影。它也被称为“极线伪圆柱投影(Robinson projection)”,因为南北两极变成两条直线而不是其它投影方法中的极点。国家地理学会1988年在他们的世界地图上采用了这一方法,但在10年后废弃了这一投影改用Winkel Tripel投影。许多教育机构和教科书跟着国家地理学会采用了这一投影,且大多数仍在采用。
和其它投影方法一样,罗宾森投影有优点也有缺点。这种投影方法不是等积方法,也没有做到共形映射。放弃这两点的同时,创造者希望能构建更好的整体视觉效果并可以尽量达到平衡。经度缓缓地弯曲,避免了巨大变化。因而将两极拉长到一条线而不是合成一点。因此两极的变形较厉害,但离两极不远的地方就很快回到了适当的水平。在地图外侧的高纬度区域有较严重的角度变形,这是在任何伪圆柱投影都存在的内在缺陷。但是,这种投影方法在研究出来时,有效地达到了兰德麦奈利出版社想要美观描述整个世界的目的。
这一投影方法由以下表格进行定义:
| 纬度 | PLEN | PDFE |
|---|---|---|
| 00 | 1.0000 | 0.0000 |
| 05 | 0.9986 | 0.0620 |
| 10 | 0.9954 | 0.1240 |
| 15 | 0.9900 | 0.1860 |
| 20 | 0.9822 | 0.2480 |
| 25 | 0.9730 | 0.3100 |
| 30 | 0.9600 | 0.3720 |
| 35 | 0.9427 | 0.4340 |
| 40 | 0.9216 | 0.4958 |
| 45 | 0.8962 | 0.5571 |
| 50 | 0.8679 | 0.6176 |
| 55 | 0.8350 | 0.6769 |
| 60 | 0.7986 | 0.7346 |
| 65 | 0.7597 | 0.7903 |
| 70 | 0.7186 | 0.8435 |
| 75 | 0.6732 | 0.8936 |
| 80 | 0.6213 | 0.9394 |
| 85 | 0.5722 | 0.9761 |
| 90 | 0.5322 | 1.0000 |
这一表格使用纬度进行索引,并使用了插值的方法。PLEN列是纬线的长度,而PDFE列乘于0.5072可以得到纬线到赤道的距离。同一纬度的经度之间距离相等。
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.