函数图形

在数学中，函数 f 的图形（或图像）指的是所有有序对(x, f(x))组成的集合。具体而言，如果x为实数，则函数图形在平面直角坐标系上呈现为一条曲线。如果函数自变量x为两个实数组成的有序对(x₁, x₂)，则图形就是所有三重序(x₁, x₂, f(x₁, x₂))组成的集合，呈现为曲面（参见三维计算机图形）。

函数 ${\displaystyle f(x)=x^{2}}$ 的图形

sin(x)等函数的图形

实函数的图形拥有其唯一的图像。而对于一般的函数，其图形形式无法应用，图形的正式定义取决于数学表述的需要，例如泛函分析中的闭图像定理。

函数图形的概念由二元关系图形推广而来。需要注意的是，尽管一个函数与其图像通常是一一对应的，但二者并不可混淆。两个函数可能拥有相同的图像，却有不同的上域。例如，对于下文提到的三次多项式，当其上域为实数时函数即为满射，而若其上域为复数则不然。

通过垂线测试可以判断一条曲线是否为一个函数，而通过水平线测试可以判断函数是否为单射且是否存在反函数。如果反函数存在，则其图像可以通过将原函数图像以直线y=x为轴进行对称得到。

样例

单变量函数

一次函数

三个线性函数的图形都是直线。红色与蓝色直线的斜率相同。 红色与绿色直线的 y-截距相同

参见：线性函数

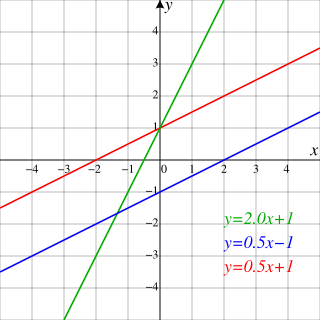
形如

${\displaystyle f(x)=kx+b\!\ }$

的图像为：

${\displaystyle \left\{(x,kx+b)|x\in \mathbb {R} \right\}}$

在平面直角坐标系中，该图像为一条直线。这是因为，该函数的导数为常数${\displaystyle k}$。

非线性函数

函数 ${\displaystyle f(x)=x^{3}-9x}$ 的图像

对于二次或更高次的多项式函数，或者其他的非线性函数，其图像则会呈现为一条曲线。这是因为其导函数不是常数函数。

例如，三次函数

${\displaystyle f(x)={{x^{3}}-9x}\!\ }$

的图像为

${\displaystyle \left\{(x,x^{3}-9x)|x\in \mathbb {R} \right\}}$

如果将这个图像绘制在平面直角坐标系中，则会得到一条三次曲线（见右图）。

双变量函数

函数 ${\displaystyle {\begin{smallmatrix}f(x,y)=\sin(x^{2})\times \cos(y^{2})\end{smallmatrix}}}$ 的图像

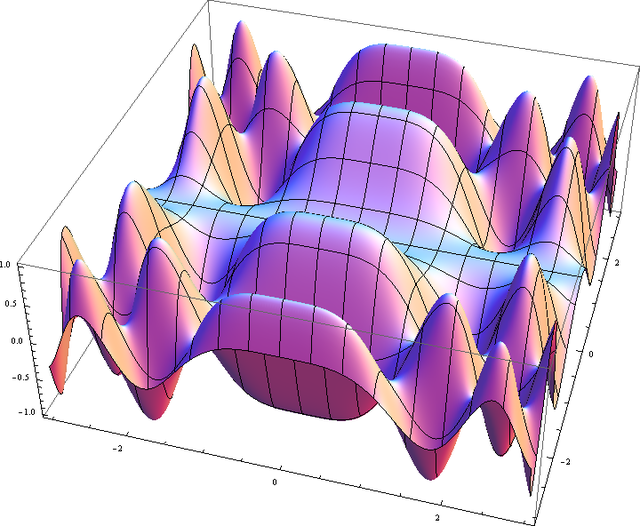
三角学中的函数

${\displaystyle f(x,y)=\sin x^{2}\cos y^{2}}$

的图像为

${\displaystyle \left\{(x,y,\sin x^{2}\cos y^{2})|x,y\in \mathbb {R} \right\}}$

如果这个图像绘制在了三维坐标系中，则会得到一个曲面（见图）。

函数图像绘制工具

硬件

TI-83绘图计算器

• 图形计算器
• 示波器

软件

更多信息：动态几何软件

参考文献

• Weisstein, Eric W. "Function Graph - MathWorld （页面存档备份，存于互联网档案馆）."

相关条目

• 函数
• 导数
• 驻点
• 斜率
• 截距
• 方程
• 坐标系