九点圆定理

九点圆定理指出：在平面中，对所有三角形，其三边的中点、三高的垂足、顶点到垂心的三条线段的中点，必然共圆，这个圆被称为九点圆，又称欧拉圆、费尔巴哈圆。

九点圆

九点圆具有以下性质：

• 九点圆的半径是外接圆的一半。
• 圆心在欧拉线上，且在垂心到外心的线段的中点。
• 九点圆和三角形的内切圆和旁切圆相切（费尔巴哈定理）。
• 圆周上四点任取三点做三角形，四个三角形的九点圆圆心共圆（柯立芝-大上定理）^{[来源请求]}。

历史

1765年，莱昂哈德·欧拉证明：“垂心三角形和垂足三角形有共同的外接圆（六点圆）。”许多人误以为九点圆是由欧拉发现所以又称乎此圆为欧拉圆。而第一个证明九点圆的人是彭赛列（1821年）。1822年，卡尔·威廉·费尔巴哈也发现了九点圆，并得出“九点圆和三角形的内切圆和旁切圆相切”，因此德国人称此圆为费尔巴哈圆，并称这四个切点为费尔巴哈点。柯立芝与大上茂乔（Shigetaka Ooue）^[1]分别于1910年与1916年发表“圆周上四点任取三点做三角形，四个三角形的九点圆圆心共圆。”这个圆还被称为四边形的九点圆，此结果还可推广到n边形。

九点圆证明

如图：${\displaystyle D}$、${\displaystyle E}$、${\displaystyle F}$为三边的中点，${\displaystyle G}$、${\displaystyle H}$、${\displaystyle I}$为垂足，${\displaystyle J}$、${\displaystyle K}$、${\displaystyle L}$为和顶点到垂心的三条线段的中点。

• 容易得出${\displaystyle \triangle ABS\sim \triangle AFJ}$、${\displaystyle \triangle CBS\sim \triangle CDL}$（${\displaystyle SAS}$相似）

• 因此${\displaystyle {\overline {FJ}}//{\overline {BH}}//{\overline {DL}}}$

• 同样可得出${\displaystyle \triangle ABC\sim \triangle FBD}$、${\displaystyle \triangle ASC\sim \triangle JSL}$（${\displaystyle SAS}$相似）

• 因此${\displaystyle {\overline {FD}}//{\overline {AC}}//{\overline {JL}}}$

• 又${\displaystyle {\overline {BH}}\perp {\overline {AC}}}$，可得出四边形${\displaystyle DFJL}$是矩形（四点共圆）

• 同理可证${\displaystyle FKLE}$也是矩形（${\displaystyle DKFJEL}$共圆）

• ${\displaystyle \angle JLD=\angle JGD=90^{\circ }}$，因此可知${\displaystyle G}$也在圆上（圆周角相等）

• 同理可证${\displaystyle H}$、${\displaystyle I}$两点也在圆上（九点共圆）

性质证明

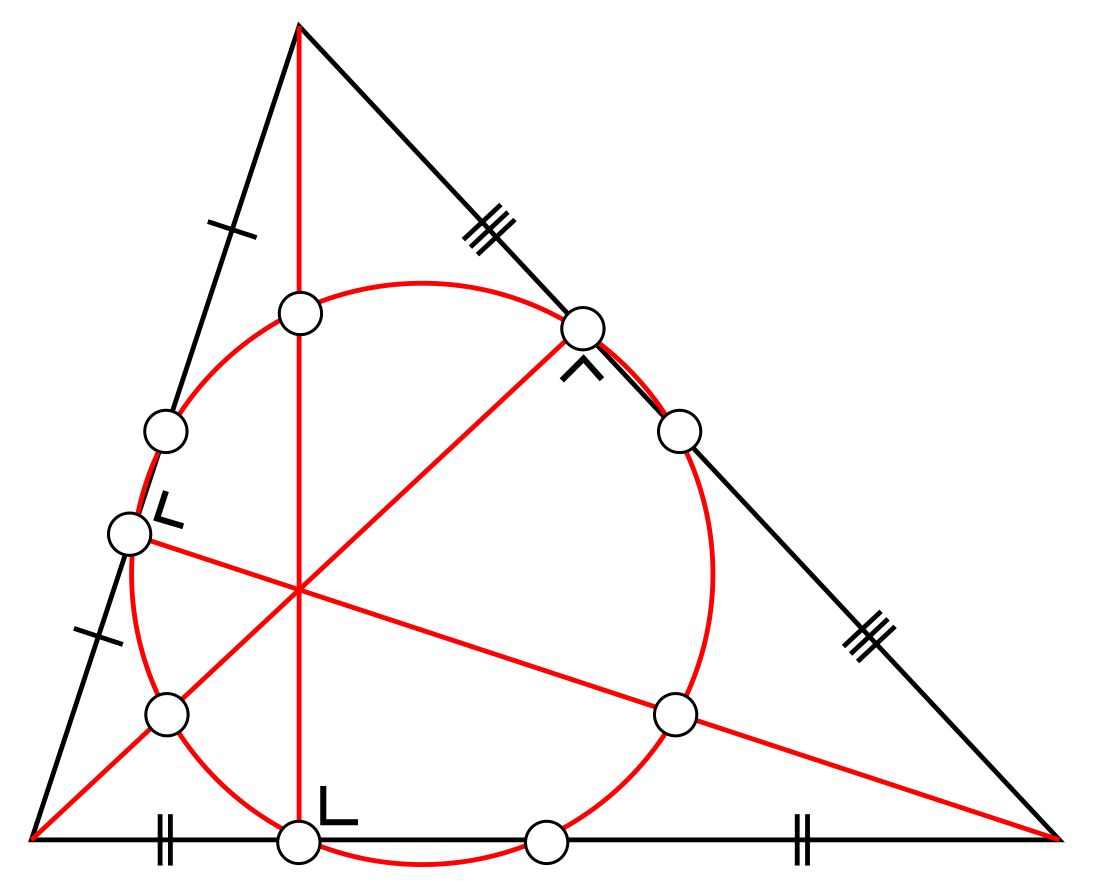
九点圆的半径是外接圆的一半，且九点圆平分垂心与外接圆上的任一点的连线。

• 在直角坐标系中，已知圆的方程为${\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}=r^{2}}$，其中${\displaystyle r}$为圆的半径，${\displaystyle (x_{0},y_{0})}$为圆的圆心坐标。若做圆上三点与点${\displaystyle (x_{S},y_{S})}$的中点的轨迹，则此轨迹的方程式为：

${\displaystyle \left(x-{\frac {x_{0}+x_{S}}{2}}\right)^{2}+\left(y-{\frac {y_{0}+y_{S}}{2}}\right)^{2}=\left({\frac {r}{2}}\right)^{2}}$

• 设${\displaystyle r}$为外接圆的半径、${\displaystyle (x_{0},y_{0})}$为外接圆的圆心坐标、点${\displaystyle (x_{S},y_{S})}$为垂心坐标。
• 已知九点圆通过顶点到垂心的三条线段的中点，故此轨迹圆就是九点圆，半径是外接圆的一半，且平分垂心与外接圆上的任一点的连线。
• 同时还可以得出下面的性质：

• 圆心在欧拉线上，且在垂心到外心的线段的中点。由此可知，给定三角形顶点坐标，九点圆圆心为

${\displaystyle \left({\frac {\begin{vmatrix}x_{1}^{2}+y_{1}^{2}-2\left(x_{2}x_{3}+y_{2}y_{3}\right)&y_{1}&1\\x_{2}^{2}+y_{2}^{2}-2\left(x_{3}x_{1}+y_{3}y_{1}\right)&y_{2}&1\\x_{3}^{2}+y_{3}^{2}-2\left(x_{1}x_{2}+y_{1}y_{2}\right)&y_{3}&1\\\end{vmatrix}}{4{\begin{vmatrix}x_{1}&y_{1}&1\\x_{2}&y_{2}&1\\x_{3}&y_{3}&1\end{vmatrix}}}},{\frac {\begin{vmatrix}x_{1}&x_{1}^{2}+y_{1}^{2}-2\left(x_{2}x_{3}+y_{2}y_{3}\right)&1\\x_{2}&x_{2}^{2}+y_{2}^{2}-2\left(x_{3}x_{1}+y_{3}y_{1}\right)&1\\x_{3}&x_{3}^{2}+y_{3}^{2}-2\left(x_{1}x_{2}+y_{1}y_{2}\right)&1\\\end{vmatrix}}{4{\begin{vmatrix}x_{1}&y_{1}&1\\x_{2}&y_{2}&1\\x_{3}&y_{3}&1\end{vmatrix}}}}\right)}$

• 九点圆和三角形的内切圆和旁切圆相切（费尔巴哈定理）。

主条目：费尔巴哈定理

• 圆周上四点任取三点做三角形，四个三角形的九点圆圆心共圆。

其他

• 垂心四面体的12点共球九点圆是垂心四面体各棱的中点和垂足（相对于对棱）共球的特例，两者是同构的
• 主旁心三角形的九点圆是三角形的外接圆
• 中点三角形的外接圆是三角形的九点圆
• 三线坐标中，九点圆的坐标为${\displaystyle \cos(B-C)\,:\,\cos(C-A)\,:\,\cos(A-B)}$
• 三线坐标中，费尔巴哈点的坐标为${\displaystyle 1-\cos(B-C)\,:\,1-\cos(C-A)\,:\,1-\cos(A-B)}$

参见条目

• 莱昂哈德·欧拉
• 卡尔·威廉·费尔巴哈