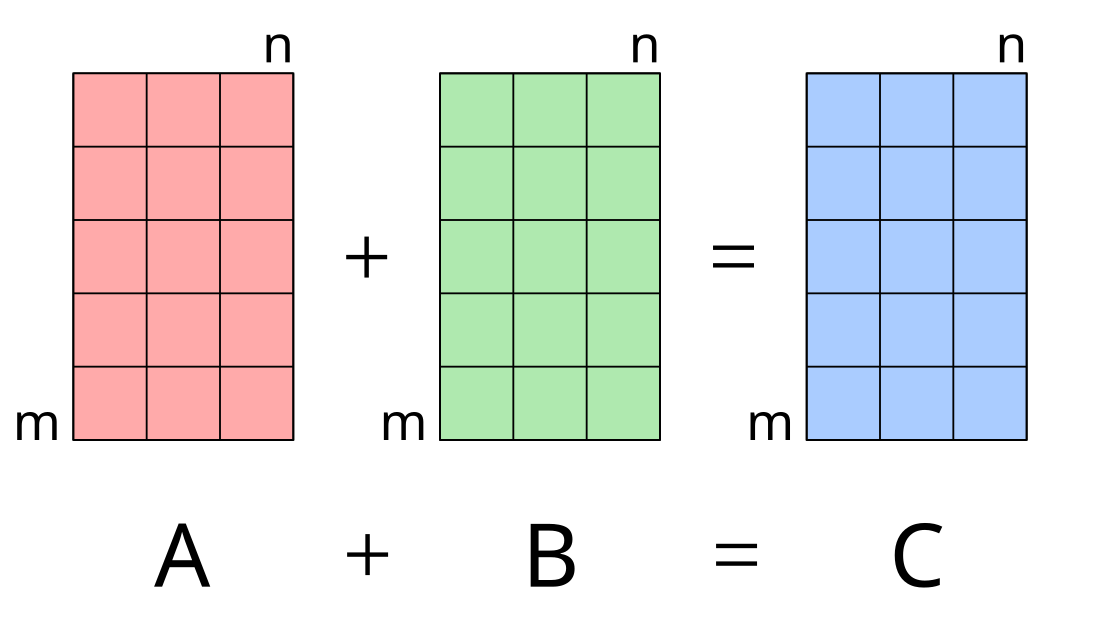
Phép cộng ma trận

Trong toán học, phép cộng ma trận là phép toán cộng hai ma trận bằng cách cộng các phần tư tương ứng với nhau. Tuy nhiên, có những phép toán khác cũng có thể được coi là cộng ma trận, chẳng hạn như tổng trực tiếp và tổng Kronecker.

Một ví dụ về phép cộng ma trận

Tổng phần tử

Hai ma trận phải có số hàng và số cột bằng nhau để thực hiện được phép tính.^[1] Trong trường hợp đó, tổng của hai ma trận A và B sẽ là ma trận có cùng số hàng và số cột như Avà B. Tổng của A và B, được biểu thị A + B,^[2] được tính bằng cách cộng các phần tử tương ứng của A và B:^[3][4]

${\displaystyle {\begin{aligned}\mathbf {A} +\mathbf {B} &={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{bmatrix}}+{\begin{bmatrix}b_{11}&b_{12}&\cdots &b_{1n}\\b_{21}&b_{22}&\cdots &b_{2n}\\\vdots &\vdots &\ddots &\vdots \\b_{m1}&b_{m2}&\cdots &b_{mn}\\\end{bmatrix}}\\&={\begin{bmatrix}a_{11}+b_{11}&a_{12}+b_{12}&\cdots &a_{1n}+b_{1n}\\a_{21}+b_{21}&a_{22}+b_{22}&\cdots &a_{2n}+b_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}+b_{m1}&a_{m2}+b_{m2}&\cdots &a_{mn}+b_{mn}\\\end{bmatrix}}\\\end{aligned}}\,\!}$

Hay ngắn gọn hơn (giả sử rằng A + B = C):^[5][6]

${\displaystyle c_{ij}=a_{ij}+b_{ij}}$

Ví dụ:

${\displaystyle {\begin{bmatrix}1&3\\1&0\\1&2\end{bmatrix}}+{\begin{bmatrix}0&0\\7&5\\2&1\end{bmatrix}}={\begin{bmatrix}1+0&3+0\\1+7&0+5\\1+2&2+1\end{bmatrix}}={\begin{bmatrix}1&3\\8&5\\3&3\end{bmatrix}}}$

Tương tự, cũng có thể trừ ma trận này với ma trận khác, miễn là chúng có cùng kích thước. Sự khác biệt của A và B, biểu thị là A − B,^[2] được tính bằng cách trừ đi các phần tử của B từ các phần tử tương ứng của A và có cùng kích thước với A và B. Ví dụ:

${\displaystyle {\begin{bmatrix}1&3\\1&0\\1&2\end{bmatrix}}-{\begin{bmatrix}0&0\\7&5\\2&1\end{bmatrix}}={\begin{bmatrix}1-0&3-0\\1-7&0-5\\1-2&2-1\end{bmatrix}}={\begin{bmatrix}1&3\\-6&-5\\-1&1\end{bmatrix}}}$

Tổng trực tiếp

Một phép toán khác, được sử dụng ít thường xuyên hơn, là tính tổng trực tiếp (ký hiệu ⊕). Lưu ý rằng tổng Kronecker cũng được có ký hiệu ⊕; tùy ngữ cảnh mà áp dụng. Tổng trực tiếp của bất kỳ cặp ma trận A nào có kích thước m × n và B có kích thước p × q là ma trận có kích thước (m + p) × (n + q) định nghĩa là:^[7][3]

${\displaystyle \mathbf {A} \oplus \mathbf {B} ={\begin{bmatrix}\mathbf {A} &{\boldsymbol {0}}\\{\boldsymbol {0}}&\mathbf {B} \end{bmatrix}}={\begin{bmatrix}a_{11}&\cdots &a_{1n}&0&\cdots &0\\\vdots &\ddots &\vdots &\vdots &\ddots &\vdots \\a_{m1}&\cdots &a_{mn}&0&\cdots &0\\0&\cdots &0&b_{11}&\cdots &b_{1q}\\\vdots &\ddots &\vdots &\vdots &\ddots &\vdots \\0&\cdots &0&b_{p1}&\cdots &b_{pq}\end{bmatrix}}}$

Ví dụ,

${\displaystyle {\begin{bmatrix}1&3&2\\2&3&1\end{bmatrix}}\oplus {\begin{bmatrix}1&6\\0&1\end{bmatrix}}={\begin{bmatrix}1&3&2&0&0\\2&3&1&0&0\\0&0&0&1&6\\0&0&0&0&1\end{bmatrix}}}$

Tổng trực tiếp của ma trận là một dạng đặc biệt của ma trận khối. Đặc biệt, tổng trực tiếp của các ma trận vuông là một ma trận khối chéo.

Ma trận kề của liên hợp các đồ thị (hoặc đa đồ thị s) rời nhau là tổng trực tiếp của các ma trận kề của chúng. Bất kỳ phần tử nào trong tổng trực tiếp của hai không gian vectơ của ma trận đều có thể được biểu diễn dưới dạng tổng trực tiếp của hai ma trận.

Nói chung, tổng trực tiếp của ma trận n là:^[3]

${\displaystyle \bigoplus _{i=1}^{n}\mathbf {A} _{i}=\operatorname {diag} (\mathbf {A} _{1},\mathbf {A} _{2},\mathbf {A} _{3},\ldots ,\mathbf {A} _{n})={\begin{bmatrix}\mathbf {A} _{1}&{\boldsymbol {0}}&\cdots &{\boldsymbol {0}}\\{\boldsymbol {0}}&\mathbf {A} _{2}&\cdots &{\boldsymbol {0}}\\\vdots &\vdots &\ddots &\vdots \\{\boldsymbol {0}}&{\boldsymbol {0}}&\cdots &\mathbf {A} _{n}\\\end{bmatrix}}\,\!}$

trong đó các số 0 là các khối số không (tức là các ma trận 0).

Tổng Kronecker

Bài chi tiết: Tổng Kronecker

Tổng Kronecker khác với tổng trực tiếp, nhưng cũng được biểu thị bằng ⊕. Nó được xác định bằng cách sử dụng tích Kronecker ⊗ và phép cộng ma trận thông thường. Nếu A là n × n, B là m × m và ${\displaystyle \mathbf {I} _{k}}$ biểu thị rằng ma trận đơn vị k × k thì tổng Kronecker được xác định bởi:

${\displaystyle \mathbf {A} \oplus \mathbf {B} =\mathbf {A} \otimes \mathbf {I} _{m}+\mathbf {I} _{n}\otimes \mathbf {B} .}$

Xem thêm

• Phép nhân ma trận
• Cộng vectơ

Ghi chú

1. Elementary Linear Algebra by Rorres Anton 10e p53
2. “Comprehensive List of Algebra Symbols”. Math Vault (bằng tiếng Anh). ngày 25 tháng 3 năm 2020. Truy cập ngày 7 tháng 9 năm 2020.
3. Lipschutz & Lipson.Lỗi sfn: không có mục tiêu: CITEREFLipschutzLipson (trợ giúp)
4. Riley, K.F.; Hobson, M.P.; Bence, S.J. (2010). Mathematical methods for physics and engineering. Cambridge University Press. ISBN 978-0-521-86153-3.
5. Weisstein, Eric W. “Matrix Addition”. mathworld.wolfram.com (bằng tiếng Anh). Truy cập ngày 7 tháng 9 năm 2020.
6. “Finding the Sum and Difference of Two Matrices | College Algebra”. courses.lumenlearning.com. Truy cập ngày 7 tháng 9 năm 2020.
7. Weisstein, Eric W., "Matrix Direct Sum" từ MathWorld.

Tham khảo

• Lipschutz, S.; Lipson, M. (2009). Linear Algebra. Schaum's Outline Series. ISBN 978-0-07-154352-1.

Liên kết ngoài

• Direct sum of matrices tại trang PlanetMath.org.
• Abstract nonsense: Direct Sum of Linear Transformations and Direct Sum of Matrices
• Mathematics Source Library: Arithmetic Matrix Operations
• Matrix Algebra and R