Orbital phân tử

Trong hóa học orbital phân tử (tiếng Anh: molecular orbital, viết tắt: MO) là hàm số toán học mô tả dáng điệu tựa như sóng của một điện tử trong một phân tử. Hàm số này có thể được sử dụng để tính toán các tính chất hóa học và vật lý như xác suất tìm electron ở bất kỳ vùng cụ thể nào.

Tập hợp orbital phân tử của acetylen (H–C≡C–H). Bên trái là MO đang ở trạng thái cơ bản, với trên cùng là quỹ đạo năng lượng thấp nhất. Đường màu trắng và màu xám có thể nhìn thấy trong một số MO là trục phân tử đi qua hạt nhân. Các hàm sóng orbital là dương ở vùng màu đỏ và âm ở màu lam. Cột bên phải cho thấy các MO ảo bị trống rỗng trong trạng thái nền, nhưng có thể bị chiếm trong các trạng thái kích thích.

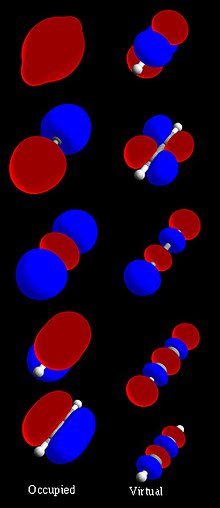
Thuật ngữ orbital được Robert S. Mulliken đề xuất năm 1932 như là viết tắt cho hàm số sóng orbital cho một electron ^[1]. Ở một mức cơ bản, nó được sử dụng để mô tả vùng không gian trong đó hàm số có biên độ đáng kể. Các orbital phân tử thường được xây dựng bằng cách kết hợp quỹ đạo nguyên tử hoặc orbital lai từ mỗi nguyên tử của phân tử, hoặc các orbital phân tử khác từ các nhóm nguyên tử. Chúng có thể được định lượng bằng cách sử dụng phương pháp Hartree-Fock hay phương pháp trường tự tương hợp (tạm dịch: SCF, self-consistent field).

Tổng quan

Một orbital phân tử (MO) có thể được sử dụng để biểu diễn các vùng trong một phân tử nơi một điện tử chiếm được orbital đó có thể sẽ được tìm thấy. Orbital phân tử thu được từ sự kết hợp của orbital nguyên tử, mà nó dự đoán vị trí của một điện tử trong nguyên tử. Một orbital phân tử có thể xác định cấu hình electron của một phân tử: sự phân bố không gian và năng lượng của một (hoặc một cặp) electron. Thông thường orbital phân tử được thể hiện như một tổ hợp tuyến tính các quỹ đạo nguyên tử (phương pháp LCAO-MO), đặc biệt là trong việc sử dụng định tính hoặc xấp xỉ gần. Chúng rất có giá trị trong việc cho ra một mô hình đơn giản của liên kết trong các phân tử, được hiểu qua lý thuyết orbital phân tử.

Hầu hết các phương pháp ngày nay trong Hóa học tính toán bắt đầu bằng cách tính các orbital phân tử của hệ thống. Một orbital phân tử mô tả hành vi của một điện tử trong trường điện tạo ra bởi các hạt nhân và một số phân bố trung bình của các electron khác. Trong trường hợp có hai điện tử chiếm cùng một orbital, nguyên lý Pauli đòi hỏi chúng phải có spin ngược nhau. Điều này là cần thiết, và các mô tả chính xác cao về hàm sóng điện tử phân tử không có orbital (xem tương tác cấu hình).

Tham khảo

1. Mulliken, Robert S. (tháng 7 năm 1932). “Electronic Structures of Polyatomic Molecules and Valence. II. General Considerations”. Physical Review. 41 (1): 49–71. Bibcode:1932PhRv...41...49M. doi:10.1103/PhysRev.41.49.

Xem thêm

• Quỹ đạo nguyên tử (AO, Atomic orbital)
• Lý thuyết quỹ đạo phân tử (MO, Molecular orbital theory)
• Tương tác cấu hình (Configuration Interaction)
• Tổ hợp tuyến tính các quỹ đạo nguyên tử (LCAO, Linear combination of atomic orbitals)

Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Orbital phân tử.

Liên kết ngoài

• Java molecular orbital viewer shows orbitals of hydrogen molecular ion.
• The orbitron, a visualization of all atomic, and some molecular and hybrid orbitals
• xeo Visualizations of some atomic and molecular atoms
• OrbiMol Molecular orbital database.