Hàm zeta Riemann

Hàm zeta Riemann hoặc hàm zeta Euler-Riemann, ζ(s), là một hàm số một biến phức, là kết quả thác triển giải tích của chuỗi Dirichlet

${\displaystyle \zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}}$

Tính chất cơ bản
Miền xác định	${\displaystyle \mathbb {C} \setminus \{1\}}$
Miền đích	${\displaystyle \mathbb {C} }$
Giá trị cụ thể
Tại số 0	${\displaystyle -{\frac {1}{2}}}$
Giá trị tại +∞	${\displaystyle 1}$
Giá trị tại ${\displaystyle 2}$	${\displaystyle {\frac {\pi ^{2}}{6}}}$
Giá trị tại ${\displaystyle -1}$	${\displaystyle -{1 \over 12}}$
Giá trị tại ${\displaystyle -2}$	${\displaystyle 0}$

Điểm kì dị tại ${\displaystyle z=1}$ và hai không điểm trên đường tới hạn.

Chuỗi này hội tụ khi phần thực của s lớn hơn 1. Thác triển giải tích tối đại của nó được xác định trên toàn bộ mặt phẳng phức trừ điểm 1. Hàm zeta Riemann đóng vai trò then chốt trong lý thuyết số giải tích và có các ứng dụng trong vật lý, lý thuyết xác suất và thống kê ứng dụng.

Định nghĩa

Bài báo của Bernhard Riemann Về số lượng các số nguyên tố dưới một độ lớn nhất định.

Hàm zeta Riemann ζ(s) là một hàm số một biến phức s = σ + i t.

Đối với trường hợp đặc biệt ${\displaystyle \,{\mathfrak {Re}}(s)\equiv \sigma >1\,}$, hàm zeta có thể được biểu thị bằng tích phân sau:

${\displaystyle \zeta (s)={\frac {1}{\Gamma (s)}}\int _{0}^{\infty }{\frac {x^{s-1}}{e^{x}-1}}\,\mathrm {d} \,x\quad {\text{ với }}\quad {\mathfrak {Re}}(s)\equiv \sigma >1}$

trong đó

${\displaystyle \Gamma (s)=\int _{0}^{\infty }x^{s-1}\,e^{-x}\,\mathrm {d} \,x}$

là hàm gamma.

Trong trường hợp σ > 1, tích phân trên luôn hội tụ, và có thể được đơn giản hóa bằng chuỗi vô hạn:

${\displaystyle \zeta (s)=\sum _{n=1}^{\infty }n^{-s}={\frac {1}{1^{s}}}+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+\cdots \quad {\text{ với }}\quad \sigma \equiv {\mathfrak {Re}}(s)>1\,.}$

Hàm zeta Riemann được định nghĩa là thác triển giải tích của hàm trên.

Với s = 1, chuỗi trên là chuỗi điều hòa phân kỳ và

${\displaystyle \lim _{s\to 1}~(s-1)\,\zeta (s)=1\,.}$

Như vậy hàm zeta Riemann là một hàm phân hình trên toàn bộ mặt phẳng phức với một cực đơn tại s = 1 có thặng dư bằng 1.

Giá trị cụ thể

Với mọi số nguyên dương chẵn 2n:

${\displaystyle \zeta (2n)={\frac {(-1)^{n+1}B_{2n}(2\pi )^{2n}}{2(2n)!}}}$

trong đó B_2n là số Bernoulli thứ 2n.

Thông qua thác triển giải tích, người ta có thể chỉ ra rằng:

• ${\displaystyle \zeta (-1)=-{\tfrac {1}{12}}}$
• ${\displaystyle \zeta (0)=-{\tfrac {1}{2}};}$
• ${\displaystyle \zeta (1)=1+{\tfrac {1}{2}}+{\tfrac {1}{3}}+\cdots =\infty$ ;}
• ${\displaystyle \zeta (2)=1+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots ={\frac {\pi ^{2}}{6}}\approx 1.64493406684822643647;\!}$ 
• ${\displaystyle \zeta (4)=1+{\frac {1}{2^{4}}}+{\frac {1}{3^{4}}}+\cdots ={\frac {\pi ^{4}}{90}}\approx 1.08232323371113819152;}$ 

Giá trị này xuất hiện khi tích phân định luật Planck để rút ra định luật Stefan-Boltzmann trong vật lý.

Công thức tích Euler

Liên hệ giữa hàm zeta và số nguyên tố được phát hiện bởi Euler, người đã chứng minh đồng nhất thức

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{s}}}=\prod _{p{\text{ nguyên tố}}}{\frac {1}{1-p^{-s}}},}$

Phương trình hàm Riemann

Hàm zeta thỏa mãn phương trình hàm sau đây:

${\displaystyle \zeta (s)=2^{s}\pi ^{s-1}\ \sin \left({\frac {\pi s}{2}}\right)\ \Gamma (1-s)\ \zeta (1-s),}$

trong đó Γ(s) là hàm gamma.

Không điểm, đường tới hạn và giả thuyết Riemann

Ngoài các không điểm tầm thường, hàm zeta Riemann không có không điểm ở bên phải của σ = 1 và bên trái của σ = 0.

Đồ thị của hàm zeta Riemann dọc theo đường tới hạn cho các giá trị thực của t chạy từ 0 đến 34. Năm không điểm đầu tiên trong dải tới hạn có thể nhìn thấy rõ là nơi mà các vòng xoắn đi qua gốc tọa độ.

Phần thực (màu đỏ) và phần ảo (màu xanh) của hàm zeta Riemann zeta dọc theo đường tới hạn Re (s) = 1/2. Các không điểm không tầm thường đầu tiên có thể được nhìn thấy tại Im (s) = ± 14.135, ± 21.022 và ± 25.011.

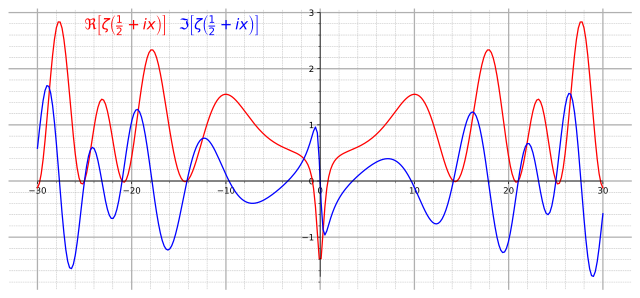
Phương trình hàm Riemann cho thấy hàm zeta Riemann có các không điểm tại −2, −4,…. Chúng được gọi là không điểm tầm thường. Chúng tầm thường theo nghĩa sự tồn tại của chúng tương đối dễ chứng minh, ví dụ, từ sin πs/2 bằng 0 trong phương trình hàm (lưu ý rằng các không điểm dương của hàm sin bị triệt tiêu bởi các cực điểm của hàm gamma).

Người ta biết rằng bất kỳ không điểm không tầm thường nào đều nằm trong dải mở {s ∈ ℂ: 0 < Re(s) < 1}, được gọi là dải tới hạn. Giả thuyết Riemann, được coi là một trong những vấn đề chưa được giải quyết lớn nhất trong toán học, khẳng định rằng bất kỳ không điểm không tầm thường s nào đều thỏa mãn Re(s) = 1/2. Trong lý thuyết về hàm zeta Riemann, tập {s ∈ ℂ: Re(s) = 1/2}   được gọi là đường tới hạn.

Ghi chú

Tham khảo

• Apostol, T. M. (2010), "Zeta and Related Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
• Borwein, Jonathan; Bradley, David M.; Crandall, Richard (2000). “Computational Strategies for the Riemann Zeta Function” (PDF). J. Comp. App. Math. 121 (1–2): 247–296. Bibcode:2000JCoAM.121..247B. doi:10.1016/S0377-0427(00)00336-8. Bản gốc (PDF) lưu trữ ngày 25 tháng 9 năm 2006. Truy cập ngày 26 tháng 7 năm 2020.
• Cvijović, Djurdje; Klinowski, Jacek (2002). “Integral Representations of the Riemann Zeta Function for Odd-Integer Arguments”. J. Comp. App. Math. 142 (2): 435–439. Bibcode:2002JCoAM.142..435C. doi:10.1016/S0377-0427(02)00358-8. MR 1906742.
• Cvijović, Djurdje; Klinowski, Jacek (1997). “Continued-fraction expansions for the Riemann zeta function and polylogarithms”. Proc. Amer. Math. Soc. 125 (9): 2543–2550. doi:10.1090/S0002-9939-97-04102-6.
• Edwards, H. M. (1974). Riemann's Zeta Function. Academic Press. ISBN 0-486-41740-9. Has an English translation of Riemann's paper.
• Hadamard, Jacques (1896). “Sur la distribution des zéros de la fonction ζ(s) et ses conséquences arithmétiques”. Bulletin de la Société Mathématique de France. 14: 199–220. doi:10.24033/bsmf.545.
• Hardy, G. H. (1949). Divergent Series. Clarendon Press, Oxford.
• Hasse, Helmut (1930). “Ein Summierungsverfahren für die Riemannsche ζ-Reihe”. Math. Z. 32: 458–464. doi:10.1007/BF01194645. MR 1545177. (Globally convergent series expression.)
• Ivic, A. (1985). The Riemann Zeta Function. John Wiley & Sons. ISBN 0-471-80634-X.
• Motohashi, Y. (1997). Spectral Theory of the Riemann Zeta-Function. Cambridge University Press. ISBN 0521445205.
• Karatsuba, A. A.; Voronin, S. M. (1992). The Riemann Zeta-Function. Berlin: W. de Gruyter.
• Mező, István; Dil, Ayhan (2010). “Hyperharmonic series involving Hurwitz zeta function”. Journal of Number Theory. 130 (2): 360–369. doi:10.1016/j.jnt.2009.08.005. MR 2564902.
• Montgomery, Hugh L.; Vaughan, Robert C. (2007). Multiplicative number theory. I. Classical theory. Cambridge tracts in advanced mathematics. 97. Cambridge University Press. Ch. 10. ISBN 978-0-521-84903-6.
• Newman, Donald J. (1998). Analytic number theory. Graduate Texts in Mathematics. 177. Springer-Verlag. Ch. 6. ISBN 0-387-98308-2.
• Raoh, Guo (1996). “The Distribution of the Logarithmic Derivative of the Riemann Zeta Function”. Proceedings of the London Mathematical Society. s3–72: 1–27. arXiv:1308.3597. doi:10.1112/plms/s3-72.1.1.
• Riemann, Bernhard (1859). “Über die Anzahl der Primzahlen unter einer gegebenen Grösse”. Monatsberichte der Berliner Akademie.. In Gesammelte Werke, Teubner, Leipzig (1892), Reprinted by Dover, New York (1953).
• Sondow, Jonathan (1994). “Analytic continuation of Riemann's zeta function and values at negative integers via Euler's transformation of series” (PDF). Proc. Amer. Math. Soc. 120 (2): 421–424. doi:10.1090/S0002-9939-1994-1172954-7.
• Titchmarsh, E. C. (1986). Heath-Brown (biên tập). The Theory of the Riemann Zeta Function (ấn bản thứ 2). Oxford University Press.
• Whittaker, E. T.; Watson, G. N. (1927). A Course in Modern Analysis (ấn bản thứ 4). Cambridge University Press. Ch. 13.
• Zhao, Jianqiang (1999). “Analytic continuation of multiple zeta functions”. Proc. Amer. Math. Soc. 128 (5): 1275–1283. doi:10.1090/S0002-9939-99-05398-8. MR 1670846.

Liên kết ngoài

• Hazewinkel, Michiel biên tập (2001), “Zeta-function”, Bách khoa toàn thư Toán học, Springer, ISBN 978-1-55608-010-4
• Riemann Zeta Function, in Wolfram Mathworld — an explanation with a more mathematical approach
• Tables of selected zeros Lưu trữ 2009-05-17 tại Wayback Machine
• Prime Numbers Get Hitched A general, non-technical description of the significance of the zeta function in relation to prime numbers.
• X-Ray of the Zeta Function Visually oriented investigation of where zeta is real or purely imaginary.
• Formulas and identities for the Riemann Zeta function functions.wolfram.com
• Riemann Zeta Function and Other Sums of Reciprocal Powers, section 23.2 of Abramowitz and Stegun
• Frenkel, Edward. “Million Dollar Math Problem” (video). Brady Haran. Truy cập ngày 11 tháng 3 năm 2014.
• Mellin transform and the functional equation of the Riemann Zeta function—Computational examples of Mellin transform methods involving the Riemann Zeta Function