Đồ thị (lý thuyết đồ thị)

Trong toán học và tin học, đồ thị là đối tượng nghiên cứu cơ bản của lý thuyết đồ thị. Một cách không chính thức, đồ thị là một tập các đối tượng gọi là đỉnh nối với nhau bởi các cạnh. Thông thường, đồ thị được vẽ dưới dạng một tập các điểm (đỉnh, nút) nối với nhau bởi các đoạn thẳng (cạnh). Tùy theo ứng dụng mà một số cạnh có thể có hướng.

Bài này chỉ viết về các định nghĩa cơ bản. Để hiểu rộng hơn, xin xem lý thuyết đồ thị. Về ý nghĩa biểu diễn hàm số trên hệ tọa độ, xem đồ thị hàm số.

Một đồ thị vô hướng với 6 đỉnh (nút) và 7 cạnh.

Các định nghĩa

Trong các tài liệu, các định nghĩa trong lý thuyết đồ thị được phát biểu theo nhiều kiểu. Dưới đây là kiểu truyền thống của cuốn từ điển bách khoa này.

Đồ thị vô hướng

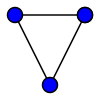
Đồ thị vô hướng hoặc đồ thị G là một cặp không có thứ tự (unordered pair) G:=(V, E), trong đó

• V, tập các đỉnh hoặc nút,
• E, tập các cặp không thứ tự chứa các đỉnh phân biệt, được gọi là cạnh. Hai đỉnh thuộc một cạnh được gọi là các đỉnh đầu cuối của cạnh đó.

Trong nhiều tài liệu, tập các cạnh bao gồm cả các cặp đỉnh không phân biệt, các cạnh này được gọi là các khuyên. V (và E) thường là các tập hữu hạn, phần lớn các kết quả nghiên cứu đã biết không đúng (hoặc khác) khi áp dụng cho đồ thị vô hạn (infinite graph) vì nhiều luận cứ không dùng được trong trường hợp vô hạn.

Đồ thị có hướng

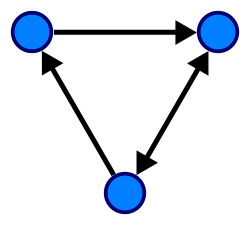
Đồ thị có hướng G là một cặp có thứ tự G:=(V, A), trong đó

• V, tập các đỉnh hoặc nút,
• A, tập các cặp có thứ tự chứa các đỉnh, được gọi là các cạnh có hướng hoặc cung. Một cạnh e = (x, y) được coi là có hướng từ x tới y; x được gọi là điểm đầu/gốc và y được gọi là điểm cuối/ngọn của cạnh.

Đơn đồ thị và Đa đồ thị

Đơn đồ thị là đồ thị mà không có khuyên và không có cạnh song song.

Đa đồ thị là đồ thị mà không thỏa mãn đơn đồ thị.

Đa đồ thị có hướng là một đồ thị có hướng, trong đó, nếu x và y là hai đỉnh thì đồ thị được phép có cả hai cung (x, y) và (y, x).

Đơn đồ thị có hướng (hoặc Đa đồ thị có hướng) là một đồ thị có hướng, trong đó, nếu x và y là hai đỉnh thì đồ thị chỉ được phép có tối đa một trong hai cung (x, y) hoặc (y, x).

Tham khảo