Напруження

Напрýження (механі́чне напру́ження) (англ. stress) — міра інтенсивності внутрішніх сил, що виникають у здеформованому тілі під впливом різноманітних факторів. Механічне напруження в точці тіла визначається як вектор внутрішніх сил, що діють на одиницю площі даної елементарної площадки^[1]. В Міжнародній системі одиниць напруження виражають у паскалях, Па (1 Па = 1 Н/м²), у системі МКГСС — в кгс/см² (1 кгс/см² = 0,98·10⁵ Па = 0,098066 МПа).

Фізична величина
Назва		Напруження
Вид величини		Механічна
Позначення величини		${\displaystyle \sigma }$, ${\displaystyle \tau }$
Позначення для розмірності		M L−1 T−2
Системи величин і одиниць	Одиниця		Розмірність
SI	паскаль, Па		кг⋅м−1⋅с−2
Англоамериканські	psi		фунт на квадратний дюйм (lbf/in2)

У Вікіпедії є статті про інші значення цього терміна: Напруження (значення).

Загальні положення

Залишкові напруження всередині пластикового транспортира, розподіл яких можна спостерігати у поляризованому світлі

При розгляді питання про міцність конструкції недостатньо знати лише систему сил, що діють на цю конструкцію. Необхідно знати ще її розміри та матеріал, з якого вона зроблена. На початку XIX століття Оґюстен-Луї Коші, відомий французький математик і механік, увів поняття напруження, яке одночасно характеризувало й силові фактори, що діяли в перерізі, й геометричні розміри цього перерізу. Напруження в загальному  — це вектор внутрішніх сил, що діють на одиницю площі даної елементарної площадки при стягуванні її у точку^[1].

Причинами виникнення напружень можуть бути: дія зовнішніх сил, вплив температурних полів (термічні напруження) чи перебіг у матеріалі тіла фізико-хімічних процесів. Напруження є результатом взаємодії частинок тіла під впливом зовнішніх факторів (навантажень, змін температури тощо), які прагнуть змінити взаємне розташування частинок, а напруження, що виникають при цьому, перешкоджають зміщенню частинок, обмежуючи його у більшості випадків деякою малою величиною.

Основні поняття

Рис. 1 Силові фактори, що виникають на елементарній площинці умовно розрізаного твердого тіла під дією зовнішніх навантажень ${\displaystyle F_{i}}$ за умов рівноваги

Рис. 2 Механічне напруження на елементарній площинці ${\displaystyle \Delta S}$ під впливом зовнішніх силових факторів ${\displaystyle F_{i}}$

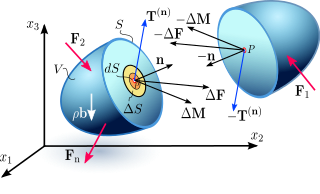
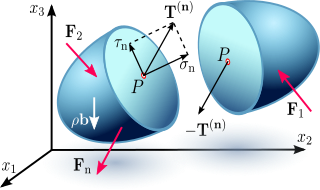
Для визначення напружень у довільному перерізі, проведеному через довільну точку тіла, застосовуємо метод перерізів. Через задану точку P (рис. 1), у якій треба визначити напруження, проведемо уявну січну площину, яка розділяє тіло на дві частини. Відкидаємо праву частину тіла і виділяємо навколо точки P елементарну площинку ΔS.

При деформуванні твердих тіл через наявність внутрішніх зв'язків у матеріалі виникають внутрішні силові фактори, котрі можна формально охарактеризувати величиною зусилля, що припадає на одиницю площі. Інтенсивність цих внутрішніх сил у певній точці називають механічним напруженням : ${\displaystyle \sigma }$, яке можна визначити як границю відношення зусилля ${\displaystyle \Delta F}$ до площі ${\displaystyle \Delta S}$, коли ця площа стягується до крапки (рис. 1).

${\displaystyle \sigma =\lim _{\Delta S\rightarrow 0}{\frac {\Delta F}{\Delta S}}.}$

Коли говорити про напруження в точці, слід вказувати його напрям, який у загальному випадку не збігається з напрямком зовнішньої нормалі до площинки. За напрям напруження приймається напрям рівнодійної ${\displaystyle \Delta F}$. Напруження в точці є величиною векторною (рис. 2).

Для випадку кінцевої площі, середнє напруження ${\displaystyle \sigma }$ на площі S можна знайти за формулою:

${\displaystyle \sigma ={\frac {F}{S}}}$

F — сила, що виникає в тілі при деформації;

S — площа перетину.

Стан елементарного об'єму тіла довкола даної точки, який характеризується сукупністю всіх векторів напружень називається напруженим станом у точці^[1].

Види напружень

Рис. 3 Нормальне напруження σ

Рис. 4 Дотичне напруження τ

Розрізняють два види компонент вектора механічного напруження^[1] (див. рис. 3 та 4):

• Нормальне напруження (напруження розтягу-стиску) — зусилля прикладене до одиниці площі перерізу зразка, спрямоване по нормалі до перерізу (позначається ${\displaystyle \sigma }$).
• Дотичне напруження (напруження зсуву) — зусилля прикладене до одиниці площі перерізу зразка, спрямоване у площині перерізу (позначається ${\displaystyle \tau }$). Поверхневе напруження - робота, необхідна для утворення одиниці площі нової поверхні при розтягуванні в рівноважних умовах. Вона чисельно рівна силі, що діє в j-тому напрямку на одиницю довжини краю, який є нормальним до і-того напрямку. Сила має бути прикладеною до кінцевої поверхні, щоб утримати її в рівновазі, при чому напрямки і-тий та j-тий повинні лежати в площині поверхні.

Поняття напруження у вигляді двох складових — нормальної та дотичної — допомагають зрозуміти види руйнування тіла. Нормальне напруження зумовлює відрив частинок однієї від іншої в умовах розтягу. Дотичне напруження відповідно зумовлює їх взаємний зсув.

Напруження, якими оперують за результатами механічних випробувань, можуть бути дійсними й умовними. Відомо, що в процесі деформації величина площини, на якій діють напруження (площа перерізу зразка), змінюється. Якщо ці зміни не враховують і напруження розглядають як відношення навантаження в даний момент до вихідної площі перерізу (S₀), то їх називають умовними напруженнями. Якщо ж відносять силу до величини фактичного перерізу в даний момент деформування, то одержують дійсне (істинне) напруження^[1]. Фізичний зміст мають лише дійсні напруження, проте на практиці часто буває зручніше користуватись умовними. Це особливо виправдано при малих деформаціях, коли зміна площі перерізу зразка є незначною.

Тензор механічних напружень

Докладніше: Тензор механічних напружень

Рис. 5 Повний тензор механічного напруження елементарного паралелепіпеда

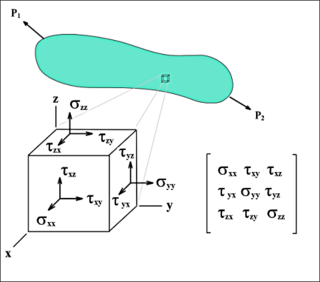
Якщо окіл точки P (рис.2) обмежити шістьма взаємно перпендикулярними площинами і отриманий елементарний паралелепіпед зорієнтувати ребрами паралельно осям декартових координат, то на кожній із граней паралелепіпеда будуть діяти відповідні напруження. Повні напруження у площинах xy, xz та yz можна розкласти по напрямах, паралельних до осей декартових координат (рис.5). Отримані дев'ять компонентів напружень повністю визначають напружений стан і утворюють тензор механічних напружень (тензор напружень Коші).

${\displaystyle {\boldsymbol {\sigma }}=\sigma _{ij}=\left[{\begin{matrix}\mathbf {T} ^{(\mathbf {e} _{1})}\\\mathbf {T} ^{(\mathbf {e} _{2})}\\\mathbf {T} ^{(\mathbf {e} _{3})}\\\end{matrix}}\right]=\left[{\begin{matrix}\sigma _{11}&\sigma _{12}&\sigma _{13}\\\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{xx}&\sigma _{xy}&\sigma _{xz}\\\sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\\sigma _{zx}&\sigma _{zy}&\sigma _{zz}\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{x}&\tau _{xy}&\tau _{xz}\\\tau _{yx}&\sigma _{y}&\tau _{yz}\\\tau _{zx}&\tau _{zy}&\sigma _{z}\\\end{matrix}}\right]\,\!}$

де

${\displaystyle \sigma _{11}\,\!}$, ${\displaystyle \sigma _{22}\,\!}$, і ${\displaystyle \sigma _{33}\,\!}$ —це нормальні напруження, а

${\displaystyle \sigma _{12}\,\!}$, ${\displaystyle \sigma _{13}\,\!}$, ${\displaystyle \sigma _{21}\,\!}$, ${\displaystyle \sigma _{23}\,\!}$, ${\displaystyle \sigma _{31}\,\!}$, і ${\displaystyle \sigma _{32}\,\!}$ є дотичними напруженнями.

У загальному випадку напружений стан характеризується тензором механічних напружень, а стан, відмінний від одновісного розтягування-стискання — складним напруженим станом.

Розкладення напруженого стану на дві базові складові

Будь-який напружений стан можна розкласти на дві базові складові:

кульову — гідростатичний тиск (кульовий тензор напружень) — обумовлює зміну об'єму (густини) тіла;

девіаторну — стан чистого зсуву (девіатор напружень) — викликає зміну форми тіла.

${\displaystyle {\begin{matrix}{\begin{bmatrix}\sigma _{11}&\sigma _{12}&\sigma _{13}\\\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\end{bmatrix}}\\\,\end{matrix}}{\begin{matrix}=\\\,\end{matrix}}\underbrace {\begin{matrix}{\begin{bmatrix}\sigma _{0}&0&0\\0&\sigma _{0}&0\\0&0&\sigma _{0}\end{bmatrix}}\\\,\end{matrix}} _{\text{кульовий тензор}}{\begin{matrix}+\\\,\end{matrix}}\underbrace {\begin{matrix}{\begin{bmatrix}\sigma _{11}-\sigma _{0}&\sigma _{12}&\sigma _{13}\\\sigma _{21}&\sigma _{22}-\sigma _{0}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}-\sigma _{0}\end{bmatrix}}\\\,\end{matrix}} _{\text{девіатор}},}$

де:

${\displaystyle \sigma _{0}={\frac {\sigma _{11}+\sigma _{22}+\sigma _{33}}{3}}.}$

Закон парності дотичних напружень

Рис. 6 Рівновага виділеного паралелепіпеда у площині xOy

Закон парності дотичних напружень: на двох довільних взаємно перпендикулярних площинах, дотичні напруження, які перпендикулярні до лінії перетину площин, рівні за величиною і протилежні за знаком ${\displaystyle (\tau _{xy}=\tau _{yx},\tau _{zy}=\tau _{yz},\tau _{xz}=\tau _{zx})}$.

Доведення

Розглянемо рівняння рівноваги виділеного елементарного паралелепіпеда у вигляді суми моментів сил відносно осей координат, що повинні дорівнювати нулю. Запишемо рівняння суми моментів сил відносно осі Oz (рис. 6):

${\displaystyle \sum M(z)=\tau _{yx}dydz{\frac {dx}{2}}-\tau _{xy}dxdz{\frac {dy}{2}}+\left(\tau _{yx}+{\frac {\partial \tau _{yx}}{\partial y}}dx\right)dydz{\frac {dx}{2}}-}$

${\displaystyle -\left(\tau _{xy}+{\frac {\partial \tau _{xy}}{\partial y}}dy\right)dxdz{\frac {dy}{2}}=0}$

Моменти відносно осі Oz від нормальних сил відсутні. Із записаного рівняння випливає

${\displaystyle \tau _{xy}=\tau _{yx}}$.

За аналогією для двох інших осей Ox та Oy:

${\displaystyle \sum M(x)=0\Rightarrow \tau _{zy}=\tau _{yz}}$

${\displaystyle \sum M(y)=0\Rightarrow \tau _{zx}=\tau _{xz}}$

Головні напруження

Докладніше: Головне напруження

Рис. 7 Залежність напружень на гранях паралелепіпеда від орієнтації координатних осей на прикладі плоского напруженого стану

При зміні напрямку координатних осей напруження на гранях елементарного паралелепіпеда змінюються. Теоретично доведено^[2], що можна завжди знайти таке положення паралелепіпеда, коли на його гранях ${\displaystyle \tau _{xy}=\tau _{zy}=\tau _{xz}=0}$.

Площини, на яких дотичні напруження дорівнюють нулю, називаються головними. Нормальні напруження, що діють на головних площинах, називаються головними напруженнями (див. рис. 7).

Головні напруження позначаються: ${\displaystyle \sigma _{1},\sigma _{2},\sigma _{3}}$ при цьому повинно виконуватись правило ${\displaystyle \sigma _{1}>\sigma _{2}>\sigma _{3}}$.

Деякі з головних напружень можуть дорівнювати нулю. В залежності від кількості відмінних від нуля головних напружень розрізняють такі види напруженого стану:

• лінійний (одновісний);
• плоский (двовісний);
• об'ємний (тривісний).

Інваріанти напруженого стану

Тензор напружень, як і кожен тензор другого порядку, має три інваріанти, тобто величини, незалежні від системи координат:

${\displaystyle I_{1}=\sigma _{1}+\sigma _{2}+\sigma _{3}=\operatorname {const} ,}$

${\displaystyle I_{2}=\sigma _{1}\cdot \sigma _{2}+\sigma _{2}\cdot \sigma _{3}+\sigma _{3}\cdot \sigma _{1}=\operatorname {const} ,}$

${\displaystyle I_{3}=\sigma _{1}\cdot \sigma _{2}\cdot \sigma _{3}=\operatorname {const} ,}$

де ${\displaystyle \sigma _{1},\;\sigma _{2},\;\sigma _{3}}$ головні напруження у точці тіла.

Концентрація напружень

Докладніше: Концентрація напружень

Концентрація напружень — збільшення напружень у твердому тілі у місцях зміни форми або порушень суцільності матеріалу^[3].

До факторів, що обумовлюють концентрацію напружень (концентраторів напружень), відносяться отвори, порожнини, тріщини, проточки, надрізи, кути, виступи, гострі краї, різь, а також нерівності та дефекти поверхні (риски, подряпини, мітки, зварні шви тощо). У місцях концентрації напружень не є справедливою гіпотеза плоских перерізів і класичні формули опору матеріалів є незастосовними. Для розподілу напружень у зоні концентрації характерною є різка зміна напруженого стану, що супроводжується швидким згасанням напружень з віддаленням від цієї зони.

Для оцінювання ступеня концентрації напружень використовують коефіцієнт концентрації напружень, який характеризує місцеве зростання напружень у зонах їх концентрації у порівнянні з номінальними значеннями.

Релаксація напружень

Докладніше: Релаксація напружень

Релакса́ція напру́жень у матеріалі — самовільне зменшення напружень, пов'язане з перерозподілом деформації між пружною і пластичною^[1].

Напруження, що зазнають релаксації або спеціально можуть бути створені при складанні вузлів машин і установок для забезпечення нормальної роботи останніх (наприклад, кріпильні з'єднання, пружні елементи), або вони неминуче виникають в процесі виготовлення деталей (технологічні напруження). Зокрема, релаксація напружень може спостерігатися при вилежуванні деталі після термічної обробки, при низькотемпературному відпуску, при змінному навантаженні в умовах заданої амплітуди деформації тощо. Дослідження показують, що релаксація напружень може відбуватися в різних матеіалах при нормальній, високих, а в ряді випадків і за низьких температур.

Релаксація напружень (подібно до повзучості) є результатом як зсувних дислокаційних, так і дифузійних процесів. Переважна роль того чи іншого явища, яке обумовлює процес релаксації, залежить від робочої температури і від рівня діючих напружень.

Див. також

• Термічні напруження
• Залишкові напруження
• Діаграма деформування
• Напружено-деформований стан
• Поверхневе напруження

Примітки

1. ДСТУ 2825-94 Розрахунки та випробування на міцність. Терміни та визначення основних понять.
2. У курсі тензорного аналізу доводиться, що при певному повороті осей тензор другого рангу завжди може бути приведений до діагонального вигляду (всі компоненти тензора, що знаходяться поза головною діагоналлю будуть дорівнювати нулю). Отже, і тензор напружень можна привести до діагонального виду. На головній діагоналі тензора напружень розташовані нормальні напруження, а поза нею — дотичні. Це означає, що для будь-якого напруженого стану існує така прямокутна система координат, в координатних площинах якої діють лише нормальні напруження, а всі дотичні напруження в цих площинах дорівнюють нулю.
3. ДСТУ 2444-94 Розрахунки та випробування на міцність. Опір втомі. Терміни та визначення.

Джерела

• Писаренко Г. С., Лебедев А. А. Деформирование и прочность материалов при сложном напряженном состоянии. — К.: Наукова думка, 1976. — 416 с.
• Опір матеріалів. Підручник / Г. С. Писаренко, О. Л. Квітка, Е. С. Уманський. За ред. Г. С. Писаренка — К.: Вища школа,1993. — 655 с. — ISBN 5-11-004083-4
• Опір матеріалів: Навч. посіб. для студентів ВНЗ. Рекомендовано МОН / Шваб'юк В. І. — К.: Знання, 2009. — 380 с.
• Мильніков О. В. Опір матеріалів. Конспект лекцій [Архівовано 20 січня 2022 у Wayback Machine.]. — Тернопіль: Видавництво ТНТУ, 2010. — 257 с.
• Божидарник В. В., Сулим Г. Т. Елементи теорії пружності. — Львів: Світ, 1994. — 560с. — ISBN 5-7773-0109-6
• Chou, Pei Chi; Pagano, N.J. (1992). Elasticity: tensor, dyadic, and engineering approaches. Dover books on engineering. Dover Publications. с. 1—33. ISBN 0-486-66958-0. Архів оригіналу за 18 серпня 2020. Процитовано 7 серпня 2019.
• Timoshenko, Stephen P. (1983). History of strength of materials: with a brief account of the history of theory of elasticity and theory of structures. Dover Books on Physics. Dover Publications. ISBN 0-486-61187-6. Архів оригіналу за 19 серпня 2020. Процитовано 7 серпня 2019.

Посилання

• Напруження механічне // Термінологічний словник-довідник з будівництва та архітектури / Р. А. Шмиг, В. М. Боярчук, І. М. Добрянський, В. М. Барабаш ; за заг. ред. Р. А. Шмига. — Львів, 2010. — С. 131. — ISBN 978-966-7407-83-4.