Надтонка структура

Надтонка структура — розщеплення спектральних ліній внаслідок взаємодії електронної оболонки атомів зі спіном ядра, а також внаслідок існування різних ізотопів елементів, що відрізняються масою та манітним моментом ядра.

Тонка надтонка структура атома водню.

Пояснення, що пов'язує ці лінії зі спіном ядра, запропонував Вольфганг Паулі.

Дослідження надтонкої структури спектральних ліній можна використати для визначення спіну ядра, наприклад, для єдиного стабільного ізотопу натрію він дорівнює 3/2 (в одиницях сталої Планка).

Надтонка структура атома цезію використовується в сучасному визначенні одиниці часу — секунди.

Історія

Перші спостереження надтонкої структури належать ще до 19 століття: 1891 року Майкельсон спостерігав її за допомогою свого інтерферометра. Після цього її описували Фабрі та Перо^[fr] 1897 року^[1], а пізніше — Люммер^[ru] та Герке^{[en] [2]}. Виявилося, що кожна спектральна лінія, насправді, складається з багатьох (до 10 й більше) компонент.

Паралельно з цим, 1910 року було відкрито ізотопію радіоактивних, а 1912 року — і нерадіоактивних елементів. 1918 року Аронберг зміг експериментально виявити ізотопічний зсув, порівнюючи випромінювання двох зразків свинцю^[3].

1924 року Паулі припустив, що розщеплення спектральних ліній пов'язано із взаємодією магнітного моменту ядра й електронів^[1].

1925 року Гоудсміт і Уленбек відкрили спін електрона, завдяки чому в 1927—1928 роках Бак і Гоудсміт змогли теоретично інтерпретували отримані до того часу результати. Протягом наступних трьох років їх результати доповнювалися й уточнювалися багатьма вченими: у цьому напрямку працювали Фермі, Бечер^[en], Казімір, Гарґрівз та інші^[4]. Велике значення для пояснення цього явища мали точні спостереження надтонкої структури подвійної жовтої D-лінії натрію, які провели 1928 року О. М. Теренін та Л. М. Добрєцов.

На початку 30-х років надтонка структура почала активно досліджуватися, і за її допомогою було визначено спіни багатьох ядер. 1932 року було відкрито нейтрон, що дозволило вирішити деякі розбіжності між експериментальними й теоретичними даними (у першу чергу це стосується вимірів спіну ядер азоту-14, що виявився рівним одиниці, проте, виходячи з популярної в ті роки протон-електронної моделі ядра, мав би бути напівцілим — ця суперечність отримала назву «азотна катастрофа»^[5]).

1945 року голландський астроном ван де Гулст передбачив існування радіолінії випромінювання атома Гідрогену довжиною 21 см, що утворюється завдяки переходу між двома рівнями надтонкої структури^[6]. 1949 року Шкловський показав, що інтенсивність такого випромінювання від міжзоряних хмар водню є достатньою для її спостереження, а 1951 року випромінювання було відкрито експериментально. Відкриття цього випромінювання стало важливою віхою в радіоастрономії.

Завдяки точному теоретичному опису надтонкого розщеплення, Лемб і Різерфорд^[en] 1947 року показали, що лінії реальних спектрів зсунуто відносно теоретичних. Це зміщення, що отримало назву лембів зсув, виявилося пов'язаним із квантовими флуктуаціями вакууму. Відкриття лембова зсуву стало поштовхом для створення квантової електродинаміки^[7].

З 1967 року еталон секунди визначається як 9 192 631 770 періодів випромінювання, що відповідають переходу між двома рівнями надтонкої структури цезію-133^[8].

Механізми виникнення надтонкої структури

Існує кілька незалежних причин розщеплення спектральних ліній, які поєднуються й роблять картину досить складною.

Ізотопний зсув

Взаємодія між електроном і ядром визначається, у першу чергу, їх електричним зарядом, який є однаковим для різних ізотопів. Проте, електрон обертається не навколо ядра, а навколо центру мас системи «ядро—електрон», розташування якого залежить від маси ядра. Зсув енергетичного рівня, спричинений скінченною масою ядра, дорівнює ${\displaystyle \Delta T=-{\frac {m_{e}}{M}}T_{\infty }}$, де T_∞ — енергія рівня при нескінченно масивному ядрі. Завдяки розщепленню такого типу, кожна спектральна лінія розпадається на декілька ліній, відповідно до кількості ізотопів елемента. Відстань між енергетичними рівнями для різних ізотопів у такому випадку дорівнює ${\displaystyle \Delta T=m_{e}{\frac {M_{1}-M_{2}}{M_{1}M_{2}}}T_{\infty }}$.

Крім того, існує так званий «специфічний» ефект маси, що виникає, коли навколо ядра рухається багато електронів. Через принцип Паулі рух електронів навколо ядра не є незалежним, а навпаки — фази окремих електронів пов'язані між собою. Вони можуть рухатися або в протифазі (й послаблювати свою дію на ядро), або ж навпаки, підсилювати її.

Втім, ця схема пояснює лише розщеплення ліній елементів з малою й середньою атомною масою. Для важких ядер цей ефект мав би створювати дуже малі зсуви, якими можна знехтувати, тоді як експерименти, навпаки, показували, що для важких ядер ізотопний зсув дуже помітний.

Такий зсув обумовлений об'ємним ефектом. Спрощено його можна пояснити так: закон Кулона справедливий лише для точкових зарядів. Реальні ж ядра мають ненульові розміри, які зростають пропорційно кубічному кореню з кількості нуклонів у ньому. І якщо ззовні ядра потенціал буде кулонівським, то всередині ядра електрична взаємодія буде ослаблюватись. Згідно з положеннями квантової механіки, електрон перебуває не на якійсь конкретній орбіті, а, з різною густиною ймовірності може перебувати в різних місцях всередині атома, зокрема — і в його ядрі. При збільшенні розмірів ядра, імовірність, що електрон перебуватиме всередині нього, зростає, а енергія зв'язку, відповідно, зменшується^[3]. Тож для важких ядер суттєвою є зміна їхніх геометричних розмірів^[9].

Взаємодія магнітних моментів

Магнітний дипольний момент ядра залежить від орбітальних і спінових моментів нуклонів наступним чином:

	p	n
gl	1	0
gs	5.5855	-3.82629

${\displaystyle {\hat {\mu }}_{z}={\frac {e\hbar }{2m_{n}c}}\sum _{i=1}^{A}(g_{s}^{i}{\hat {s}}_{i}+g_{l}^{i}{\hat {l}}_{i})}$,

де m_n — маса нуклона, A — кількість нуклонів у ядрі, g_l, g_s — орбітальне і спінове гіромагнітне співвідношення, значення яких представлені в таблиці праворуч.^[10]

Величину ${\displaystyle {\frac {e\hbar }{2m_{n}c}}=3.1524915*10^{-18}MeV/Gs}$ називають ядерним магнетоном, і вона є природною одиницею вимірювання магнітного моменту ядра, оскільки максимальна проєкція магнітного моменту на деяку вісь завжди пропорційна ядерному магнетону. За значенням ядерний магнетон у ${\displaystyle {\frac {m_{p}}{m_{e}}}}$ (тобто, у 1836) разів менший за магнетон Бора, а тому магнітні моменти ядер також на три порядки менші за магнітні моменти електронів.

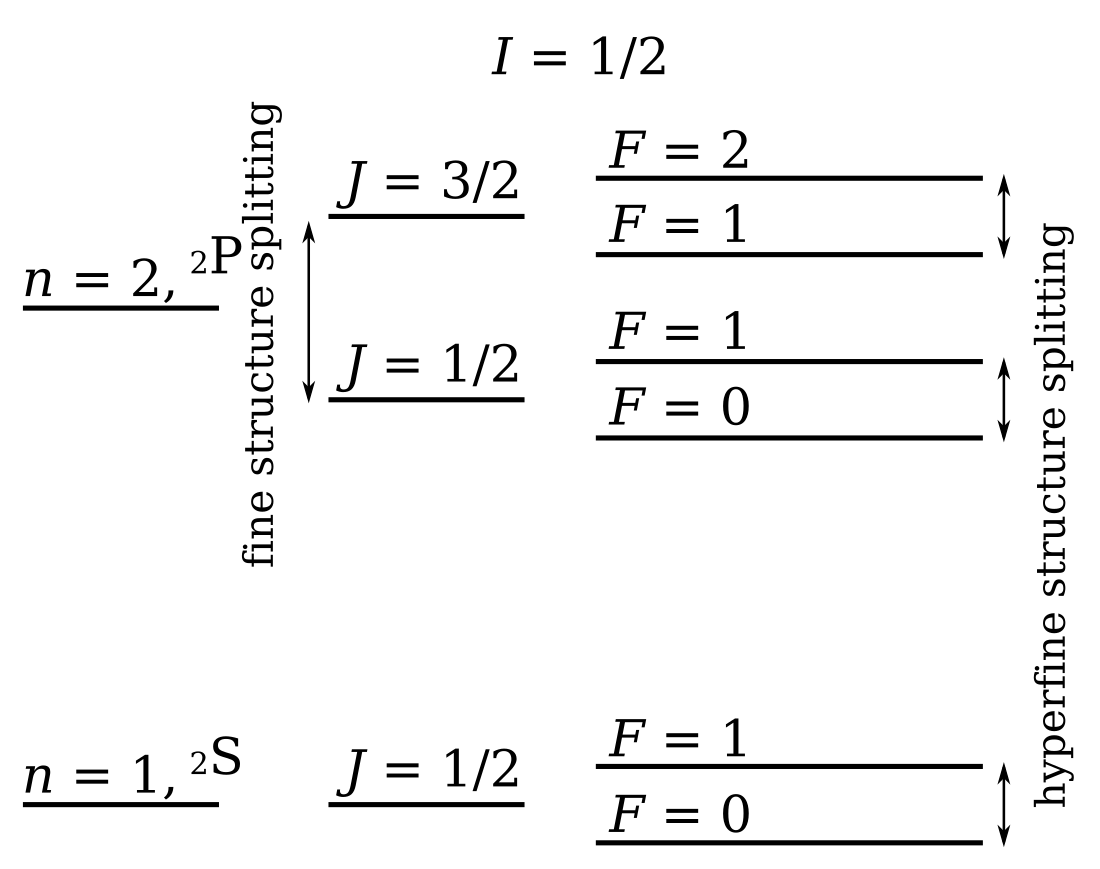
Якщо ядро атому має момент обертання I, а електрон — момент кількості руху J (що дорівнює сумі орбітального моменту й спіну), то їх сукупний момент F, залежно від їх взаємного розташування може набувати усіх цілих значень від ${\displaystyle \left|J+I\right|}$ до ${\displaystyle \left|J-I\right|}$. Відповідно, змінюється й енергія взаємодії моментів ядра й електронної оболонки, яку можна наближено подати як W=-(μ_ядраB_{електронів}). Якісно це виражається в тому, що кожен енергетичний рівень електрона, якому відповідає спектральна лінія, розділяється на 2I+1 або 2J+1 підрівнів (відповідно, якщо J більше за I, або навпаки). Виходячи з того, що взаємодія між магнітними моментами пропорційна косинусу кута між їх напрямами, величину цього розщеплення можна оцінити як

${\displaystyle \Delta W=\mu H(0){\frac {F(F+1)-I(I+1)-J(J+1)}{2IJ}}}$,

де H(0) — величина магнітного поля електронів на місці ядра, що залежить від J, та інших квантових чисел, а μ — магнітний момент ядра^[11].

Максимальна відстань між лініями, таким чином, дорівнює

${\displaystyle \Delta W=\mu H(0){\frac {2I+1}{I}}}$, якщо I≥J, або

${\displaystyle \Delta W=\mu H(0){\frac {2J+1}{J}}}$, якщо J≥I.

Правила відбору визначають, з якої підорбіталі на яку може перейти електрон, а отже і яку енергію він може при цьому випромінити. Одне з правил визначає можливі варіанти зміни F: ΔF=0, ±1, окрім випадку F₁=0, F₂=0.

За величиною надтонке розщеплення на три порядки менше за відстань між компонентами тонкої структури і для основного стану становить кілька гігагерц. Для збуджених станів надтонке розщеплення зменшується оберненно пропорційно енергії зв'язку збудженого електрона в ступені 3/2^[12].

Взаємодія з квадрупольним електричним моментом

Електричний дипольний момент ядра дорівнює нулю в основному стані, через парність квадрату його хвильової функції ядра ^[13], проте ядро (якщо воно не кулясте) має квадрупольний момент, взаємодія з яким призводить до додаткового розщеплення спектральних ліній^[14]. Квадрупольне розщеплення є значно меншим за розщеплення, пов'язане з магнітною взаємодією.

Значення

Визначення спіну ядра за допомогою аналізу надтонкої структури

При J > I, вивчення надтонкої структури спектру дозволяє легко дізнатись спін ядра — у цьому випадку, достатньо просто підрахувати кількість ліній, на які розпадається спектральна лінія: воно буде рівним 2I+1.

У випадку, коли J <= I, існують більш тонкі способи підрахувати спін ядра.

Правило інтервалів

Підрівні енергетичного рівня, яким відповідають спектральні лінії надтонкого розщеплення характеризуються одними і тими ж квантовими числами I і J, проте різними F. Відстань між підрівнями, яким відповідають квантові числа F і F+1 в такому випадку, пропорційна F+1. Таким чином, відстані між лініями надтонкої структури відносяться між собою як F:F+1:F+2 ...

Визначивши таким чином усі значення, які може набувати F, спін ядра можна визначити виходячи з того, що максимальне значення F_max=I+J.^[15]

Порівняння інтенсивностей ліній

У зовнішньому магнітному полі поведінка атома визначається сумарним моментом F, а не окремими моментами електронів і ядра, атом може орієнтуватися у ньому 2F+1 різними способами (проєкція вектора F буде приймати значення, відповідно від -F до +F). Відповідно, виродженність енергетичного підрівня також буде дорівнювати 2F+1, що, при рівності інших умов, призводить до того, що інтенсивності ліній надтонкої структури також будуть співвідноситись у тій же пропорції. Порівнюючи ці інтенсивності можна встановити F^[16].

Цей метод є менш точним, ніж правило інтервалів, а тому має сенс лише коли кількість ліній у надтонкій структурі деякого енергетичного рівня менша трьох. Такий випадок характерний для лужних металів, наприклад, натрію.

Використання для радіоастрономії

Основний рівень енергії водню розщеплюється на два близьких підрівня, залежності від того, паралельними чи антипаралельними є напрямки спінів ядра й електрона. При переході між цими рівнями випромінюється фотон з частотою 1420,4 МГц, що відповідає довжині хвилі 21,1 см. Час спонтанного переходу є значним — близько 11 мільйонів років^[6]. Температура збудження зворотнього переходу складає лише 0,068 К, тому такий перехід відбувається при зіткненнях атомів між собою або з фотонами. Як результат, у хмарах міжзоряного нейтрального водню існує динамічна рівновага між збудженим і незбудженим станом.

Хоча енергія такого випромінювання є дуже незначною, проте завдяки розповсюдженості водню у Всесвіті, дослідження випромінювання на цій частоті дає важливу інформацію про розподіл речовини в космосі.

Генератори частоти

Завдяки високій точності й стабільності, переходи між рівнями надтонкої структури застосовуються для дуже точного вимірювання часу. Поширеним варіантом є водневий генератор частоти, що використовує описаний вище перехід між рівнями надтонкої структури водню в слабкому магнітному полі, під час якого випромінюється хвиля довжиною 21,1 см. Для того, щоб атоми швидко переходили на нижній енергетичний стан, пучок атомарного водню у збудженому стані спрямовують в об'ємний резонатор, налаштований на відповідну частоту випромінювання^[17].

Складнощі експериментального дослідження

Попри дуже малу відстань між лініями, роздільної здатності навіть простих інтерферометрів, таких як інтерферометр Фабрі-Перо достатньо для їх розділення. Головною складністю при цьому є ширина самих ліній. Доплерівське розширення, зумовлене доплерівським зсувом спектрів атомів через їх тепловий рух, робить ширину ліній більшою, ніж відстань між ними^[18]. Так, наприклад, для повного розділення ліній натрію, його потрібно охолодити до 5K, що на практиці важко реалізувати — адже ці атоми постійно освітлюються. Для вирішення цієї проблеми, можна використовувати пучки швидких атомів, що рухаються перпендикулярно напрямку спостереження. Для важчих атомів швидкості теплового руху менші, тому може використовуватися звичайний тліючий розряд.

Див. також

• Тонка структура
• Надтонка взаємодія ‎

Примітки

1. Advances in Quantum Chemistry, 1965, с. 47.
2. Сивухин, 1989, с. 36.
3. ИЗОТОПИЧЕСКИЙ ЭФФЕКТ В АТОМНЫХ СПЕКТРАХ [Архівовано 8 серпня 2017 у Wayback Machine.](рос.)
4. Advances in Quantum Chemistry, 1965, с. 48.
5. Відкриття - нейтрон. Архів оригіналу за 1 вересня 2017. Процитовано 28 червня 2017.
6. Радиолиния водорода 21 см [Архівовано 1 жовтня 2020 у Wayback Machine.](рос.)
7. лэмбовский сдвиг [Архівовано 14 липня 2017 у Wayback Machine.](рос.)
8. В ПОГОНЕ ЗА ТОЧНОСТЬЮ: ЕДИНЫЙ ЭТАЛОН ВРЕМЕНИ — ЧАСТОТЫ — ДЛИНЫ [Архівовано 13 лютого 2019 у Wayback Machine.](рос.)
9. Путилов, Фабрикант, 1963, с. 323.
10. Магнитный дипольный момент ядра [Архівовано 24 червня 2017 у Wayback Machine.](рос.)
11. СВЕРХТОНКАЯ СТРУКТУРА И АТОМНОЕ ЯДРО [Архівовано 10 серпня 2017 у Wayback Machine.](рос.)
12. сверхтонкая структура [Архівовано 9 липня 2017 у Wayback Machine.](рос.)
13. Варламов, Гончарова, Ишханов, 2010, с. 28.
14. Ландау, Лифшиц, 1989, с. 579.
15. Сивухин, 1989, с. 42.
16. Сивухин, 1989, с. 43.
17. водородный генератор [Архівовано 16 липня 2019 у Wayback Machine.](рос.)
18. Сивухин, 1989, с. 37.

Література

• Advances in Quantum Chemistry / Per-Olov Löwdin. — Нью-Йорк : Academic Press Inc, 1965. — Т. 2. — 371 с. — ISBN 978-008-058-227-6.
• Глосарій термінів з хімії / укладачі: Й. Опейда, О. Швайка ; Ін-т фізико-органічної хімії та вуглехімії ім. Л. М. Литвиненка НАН України, Донецький національний університет. — Донецьк : Вебер, 2008. — 738 с. — ISBN 978-966-335-206-0.
• Путилов К.А., Фабрикант В.А. Оптика, атомная физика, ядерная физика. // Курс физики. — Друге. — М. : Государственное издательство физико-математической литературы, 1963. — Т. III. — 634 с.
• Ландау Л. Д., Лифшиц Е. М. Квантовая механика (нерелятивистская теория). // Теоретическая физика; Учеб. пособие для вузов. — 4. — М. : Наука, 1989. — Т. III. — 768 с. — ISBN 5-02-014421-5.
• Д.В. Сивухин. Часть 1. Атомная физика // Общий курс физики. — М. : Наука, 1986. — Т. V. Атомная и ядерная физика. — 426 с. — ISBN 5-02-014053-8.
• В.В.Варламов, Н.Г.Гончарова, Б.С.Ишханов. Физика ядра и банки ядерных данных. — М. : Университетская книга, 2010. — 246 с. — ISBN 978-5-91304-106-7.