Корона (теорія графів)

У теорії графів корона з 2n вершинами — неорієнтований граф із двома наборами вершин u_i та v_i і ребрами між u_i та v_j, якщо i ≠ j. Можна розглядати корону як повний двочастковий граф, з якого видалено досконале парування, як подвійне покриття дводольним графом повного графа, або як двочастковий граф Кнезера H_n,1, що представляє підмножини з 1 елемента і (n − 1) елементів множини з n елементів із ребрами між двома підмножинами, якщо одна підмножина міститься в іншій.

Корона (${\displaystyle S_{n}^{0}}$)
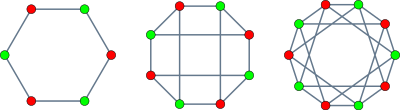Корони з шістьма, вісьмома і десятьма вершинами
Вершин	2 n
Ребер	n (n — 1)
Радіус	${\displaystyle \left\{{\begin{array}{ll}\infty &n\leq 2\\3&{\text{otherwise}}\end{array}}\right.}$
Діаметр	${\displaystyle \left\{{\begin{array}{ll}\infty &n\leq 2\\3&{\text{otherwise}}\end{array}}\right.}$
Обхват	${\displaystyle \left\{{\begin{array}{ll}\infty &n\leq 2\\6&n=3\\4&{\text{otherwise}}\end{array}}\right.}$
Хроматичне число	${\displaystyle \left\{{\begin{array}{ll}1&n=1\\2&{\text{otherwise}}\end{array}}\right.}$
Властивості	дистанційно-транзитивний

Приклади

Корона з шістьма вершинами утворює цикл, а корона з вісьмома вершинами ізоморфна графу куба. У подвійний шістці Шлефлі конфігурації 12 прямих і 30 точок у тривимірному просторі, дванадцять прямих перетинають одна одну за схемою корони з 12 вершинами.

Властивості

Біклікове покриття корони з десятьма вершинами

Число ребер у короні є прямокутним числом n(n − 1). Її ахроматичне число дорівнює n — можна знайти повне розфарбування, вибравши пару {u_i, v_i} як клас кольору^[1]. Корони є симетричними і дистанційно-транзитивними графами. Аркдікон^[en] зі співавторами^[2] описують розбиття ребер корони на цикли рівної довжини.

Корону з 2n вершинами можна вкласти в чотиривимірний евклідів простір так, що всі її ребра будуть мати довжину одиниця. Однак таке вкладення може помістити несуміжні вершини на відстань одиниця. Вкладення, за якого ребра мають довжину одиниця, а відстань між будь-якими несуміжними вершинами не дорівнює одиниці, вимагає принаймні розмірності n − 2. Це показує, що для подання графа у вигляді графа одиничних відстаней і графа строго одиничних відстаней потрібні зовсім різні розмірності^[3]. Найменше число повних двочасткових підграфів, потрібне для покриття ребер корони (її двочасткова розмірність, або розмір найменшого покриття кліками) дорівнює

${\displaystyle \sigma (n)=\min \left\{\,k\mid n\leq {\binom {k}{\lfloor k/2\rfloor }}\,\right\},}$

тобто є оберненою функцією від центрального біноміального коефіцієнта^[4].

Доповненням корони з 2n вершинами є прямий добуток повних графів K₂ ${\displaystyle \square }$ K_n, що еквівалентно туровому графу 2 × n.

Застосування

В етикеті — традиційних правилах розсаджування гостей за обіднім столом — чоловіки й жінки мають перемежовуватися і жодна сімейна пара не повинна сидіти поруч. Розсаджування, що задовольняє цим правилам для вечірки n сімейних пар, можна описати як гамільтонів цикл корони. Задача підрахунку числа можливих розсаджувань або, що майже те ж саме^[5], числа гамільтонових циклів у короні, відома в комбінаториці як задача про гостей. Для корон із числом вершин 6, 8, 10, … число (орієнтованих) гамільтонових циклів дорівнює

2, 12, 312, 9600, 416880, 23879520, 1749363840, … (послідовність A094047 з Онлайн енциклопедії послідовностей цілих чисел, OEIS)

Корони можна використовувати, щоб показати, що алгоритм жадібного розфарбовування поводиться погано в деяких випадках — якщо вершини корони надані алгоритму в порядку u₀, v₀, u₁, v₁, і т. д., то жадібне розфарбовування використовує n кольорів, хоча оптимальним числом кольорів є два. Цю побудову приписують Джонсону^[6], а самі корони іноді називають графами Джонсона з позначенням J_n^[7]. Фюрер^[8] використав корони як частину побудови, що показує складність апроксимації задачі розфарбовування.

Матушек^[9]використав відстань у коронах як приклад метричного простору, який важко вкласти в нормований векторний простір.

Як показали Миклавич і Поточник^[10], корони входять до невеликого числа різних типів дистанційно-регулярних циркулянтних графів.

Агарвал^[en] і співавтори^[11] описують многокутники, які мають корони як графи видимості. Вони використовують їх як приклад, щоб показати, що подання графів у вигляді об'єднання повних двочасткових графів не завжди ефективне щодо пам'яті.

Корона з 2n вершинами з ребрами, орієнтованими від одного боку двочасткового графа до іншого, утворює стандартний приклад частково впорядкованої множини з розмірністю упорядкування^[en] n.

Примітки

1. Amitabh Chaudhary, Sundar Vishwanathan. SODA '97: Proceedings of the 8th ACM-SIAM Symposium on Discrete Algorithms. — 1997. — С. 558—563.
2. D. Archdeacon, M. Debowsky, J. Dinitz, H. Gavlas. Cycle systems in the complete bipartite graph minus a one-factor // Discrete Mathematics^[en]. — 2004. — Т. 284, вип. 1—3. — С. 37—43. — DOI:10.1016/j.disc.2003.11.021.
3. Paul Erdős, Miklós Simonovits. On the chromatic number of geometric graphs // Ars Combinatoria. — 1980. — Т. 9. — С. 229—246.
4. Dominique de Caen, David A. Gregory, Norman J. Pullman. Proc. 3rd Caribbean Conference on Combinatorics and Computing / ред. Charles C. Cadogan. — Department of Mathematics, University of the West Indies, 1981. — С. 169—173.
5. У задачі про гостей початкова позиція циклу істотна, так що число гамільтонових циклів і розв'язок задачі про гостей відрізняються в 2n разів.
6. D. S. Johnson. Proc. 5th Southeastern Conf. on Combinatorics, Graph Theory, and Computing, Utilitas Mathematicae. — Winnipeg, 1974. — С. 513—527.
7. M. Kubale. Graph Colorings. — American Mathematical Society, 2004. — ISBN 0-8218-3458-4.
8. Fürer. Proc. 36th IEEE Symp. Foundations of Computer Science (FOCS '95). — 1995. — С. 414—421. — ISBN 0-8186-7183-1. — DOI:10.1109/SFCS.1995.492572.
9. Jiří Matoušek. On the distortion required for embedding finite metric spaces into normed spaces // Israel Journal of Mathematics. — 1996. — Т. 93, вип. 1. — С. 333—344. — DOI:10.1007/BF02761110.
10. Štefko Miklavič, Primož Poročnik. Distance-regular circulants // European Journal of Combinatorics. — 2003. — Т. 24, вип. 7. — С. 777—784. — DOI:10.1016/S0195-6698(03)00117-3.
11. Pankaj K. Agarwal, Noga Alon, Boris Aronov, Subhash Suri. Can visibility graphs be represented compactly? // Discrete and Computational Geometry. — 1994. — Т. 12, вип. 1. — С. 347—365. — DOI:10.1007/BF02574385.

Посилання

• Weisstein, Eric W. Граф корона(англ.) на сайті Wolfram MathWorld.