Закон Пуазейля

Зако́н Пуазе́йля — фізичний закон, що встановлює для ламінарної течії зв'язок між середньою швидкістю протікання рідини (або витратою) через капіляр та в'язкістю флюїду у залежності від перепаду тиску:

${\displaystyle Q={\frac {\pi R^{4}}{8\eta }}{\frac {\Delta p}{L}}}$,

Закон Пуазейля
Названо на честь	Gotthilf Hagend і Жан-Марі-Луї Пуазейль
Досліджується в	гідравліка і гідродинаміка
Закон Пуазейля у Вікісховищі

Схематичне зображення поля швидкостей для флюїду, що протікає через капіляр. Пропелери вказують завихрення.

де Q — об'єм флюїду, що протікає в одиницю часу (об'ємна витрата) через капіляр радіусом R та довжиною L при різниці тисків на кінцях капіляра ${\displaystyle \Delta p=p_{1}-p_{2}}$, ${\displaystyle \eta }$ — коефіцієнт динамічної в'язкості.

Формулюється наступним чином:

Об'ємна витрата рідини, що протікає прямолінійною ділянкою труби з круглим перетином сталого діаметра є прямо пропорційною перепаду тиску і четвертому степеню діаметра (радіуса) труби і обернено пропорційною її довжині.

Закон відкрив у 1838 Жан Марі Луї Пуазейль і, незалежно, в 1839 Ґоттгільф Гаґен.

Рівняння також відоме як закон Гаґена-Пуазейля або рівняння Пуазейля.

Основні допущення

При отриманні рівняння закону Пуазейля зроблено такі допущення:

• потік є ламінарним і одновимірним (має тільки одну компоненту швидкості) у каналі, що має вигляд прямого кругового циліндра або шару між паралельними площинами (ще має назву «потік Пуазейля»);
• рідина є ідеально в'язкою (ньютонівською) і нестисливою;
• довжина потоку суттєво більша за його поперечний розмір.

Постановка задачі

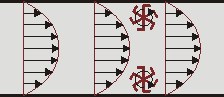
Розглядається усталений рух нестисливої рідини з постійною в'язкістю в тонкій циліндричній трубці круглого перерізу під дією постійного перепаду тиску. На основі зроблених вище допущень можна аналітично описати розподіл швидкості у потоці що має параболічний профіль (часто називають «профіль Пуазейля»), а для круглого перерізу розподіл швидкості в залежності від відстані до осі каналу:

${\displaystyle v\left(r\right)={\frac {p_{1}-p_{2}}{4\eta L}}(R^{2}-r^{2}),}$

де

• ${\displaystyle v\left(r\right)}$ — швидкість рідини на відстані r від осі труби;
• ${\displaystyle R}$ — радіус трубопроводу;
• ${\displaystyle p_{1}-p_{2}}$ — різниця тисків на вході і на виході з труби;
• ${\displaystyle \eta }$ — в'язкість рідини;
• ${\displaystyle L}$ — довжина труби.

Такий же профіль (у відповідних позначеннях) має швидкість при протіканні між двома нескінченними паралельними площинами.

Способи отримання рівняння

Шляхом інтегрування закону розподілу швидкості

Рівняння закону Пуазейля можна отримати шляхом інтегрування по площі перерізу записаного вище рівняння розподілу швидкості в залежності від радіуса для круглоциліндричної труби:

${\displaystyle Q=\int \limits _{S}v\left(r\right)dS=2\pi \int \limits _{0}^{R}v\left(r\right)rdr={\frac {\pi D^{4}(p_{1}-p_{2})}{128\eta L}}={\frac {\pi R^{4}(p_{1}-p_{2})}{8\eta L}},}$

де

• ${\displaystyle Q}$ — витрата рідини у трубопроводі;
• ${\displaystyle D}$ — діаметр трубопроводу.

На основі формули Дарсі-Вейсбаха

Такий же результат можна отримати з феноменологічної формули Дарсі-Вейсбаха, враховуючи вираз для коефіцієнта гідравлічного тертя ${\displaystyle \lambda }$ записаного через число Рейнольдса Re

${\displaystyle \lambda ={64 \over {\it {\mathrm {Re} }}}}$

де число Рейнольдса ${\displaystyle \mathrm {Re} ={2\rho VR \over \eta }.}$

З рівнянь Нав'є-Стокса

Рівняння Пуазейля можна отримати безпосередньо з рівнянь Нав'є-Стокса в циліндричних координатах, зробивши наступний набір припущень:

1. Потік є стаціонарним (${\displaystyle \partial (...)/\partial t=0}$).
2. Радіальна і вихрова компоненти швидкості рівні нулю (${\displaystyle u_{r}=u_{\theta }=0}$).
3. Потік є осесиметричним (${\displaystyle \partial (...)/\partial \theta =0}$) і повністю стабілізованим по довжині (${\displaystyle \partial u_{z}/\partial z=0}$).

Тоді друге (рівняння кута повороту) з трьох рівнянь Нав'є-Стокса у циліндричних координатах і рівняння неперервності виконуються автоматично. Перше рівняння (рівняння радіуса) спрощується до ${\displaystyle \partial p/\partial r=0}$, оскільки, тиск ${\displaystyle p}$ є лише функцією осьової координати ${\displaystyle z}$. Третє рівняння зводиться до вигляду:

${\displaystyle {\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial u_{z}}{\partial r}}\right)={\frac {1}{\mu }}{\frac {\partial p}{\partial z}}}$ де ${\displaystyle \mu }$ динамічна в'язкість рідини.

Розв'язок:

${\displaystyle u_{z}={\frac {1}{4\mu }}{\frac {\partial p}{\partial z}}r^{2}+c_{1}\ln r+c_{2}}$

З граничних умов при ${\displaystyle r=0}$, ${\displaystyle c_{1}=0}$. За відсутності ковзання на стінці труби ${\displaystyle u_{z}=0}$ при ${\displaystyle r=R}$ (радіус труби), отримаємо

${\displaystyle c_{2}=-{\frac {1}{4\mu }}{\frac {\partial p}{\partial z}}R^{2}.}$

Таким чином, отримуємо параболічний закон розподілу швидкості:

${\displaystyle u_{z}=-{\frac {1}{4\mu }}{\frac {\partial p}{\partial z}}(R^{2}-r^{2}).}$

Максимальна швидкість знаходиться на осі труби (${\displaystyle r=0}$):

${\displaystyle {u_{z}}_{max}={\frac {R^{2}}{4\mu }}\left(-{\frac {\partial p}{\partial z}}\right).}$

Середня швидкість може бути визначена шляхом інтегрування рівняння по площі перерізу:

${\displaystyle {V_{z}}_{\mathrm {cep} }={\frac {1}{\pi R^{2}}}\int _{0}^{R}u_{z}\cdot 2\pi rdr=0.5{u_{z}}_{\mathrm {max} }.}$

Знаходимо ${\displaystyle \Delta p}$ спад тиску на круглій трубі довжиною ${\displaystyle L}$, через середню швидкість потоку в трубі ${\displaystyle {V_{z}}_{\mathrm {cep} }}$ та інші параметри. Допустивши, що тиск зменшується лінійно по всій довжині труби, тобто ${\displaystyle -{\frac {\partial p}{\partial z}}={\frac {\Delta p}{L}}}$(constant). Підставивши це і вираз для ${\displaystyle {u_{z}}_{\mathrm {max} }}$ у рівняння для визначення ${\displaystyle {V_{z}}_{\mathrm {cep} }}$ та врахувавши, що ${\displaystyle D=2R}$, отримаємо

${\displaystyle {V_{z}}_{cep}={\frac {D^{2}}{32\mu }}{\frac {\Delta P}{L}}.}$

Шляхом незначних перетворень з цього рівняння отрмується рівняння закону Пуазейля.

Електро-гідравлічна аналогія

Закон Пуазейля є аналогом закону Ома для електричних кіл (V = IR), де перепад тиску ΔP виступає аналогом напруги V а об'ємна витрата потоку Q аналогом струму I. Тоді активний опір трубопроводу довжиною L і діаметром D запишеться як:

${\displaystyle R={\frac {128\eta L}{\pi D^{4}}}.}$

Використання

Закон Пуазейля використовують для визначення в'язкості флюїдів. Закон також відіграє важливу роль в таких розділах фізіології, як гемореологія та гемодинаміка.

Джерела

• Левицький Б. Ф., Лещій Н. П. Гідравліка. Загальний курс. — Львів: Світ, 1994. — 264с. ISBN 5-7773-0158-4
• Константінов Ю. М., Гіжа О. О. Технічна механіка рідини і газу: Підручник. — К.: Вища школа, 2002. — 277с.:іл. ISBN 966-642-093-7
• Кулінченко В. Р. Гідравліка, гідравлічні машини і гідропривід: Підручник.-Київ: Фірма «Інкос», Центр навчальної літератури, 2006. — 616с. ISBN 966-8347-38-2
• Колчунов В. І. Теоретична та прикладна гідромеханіка: Навч. Посібник. — К.:НАУ, 2004. — 336с. ISBN 966-598-174-9

Див. також

Формула Дарсі-Вейсбаха