Екзотичні тригонометричні функції

Екзотичні тригонометричні функції — функції кута, які в теперішній час використовуються рідше за основні тригонометричні функції (синус, косинус, тангенс, котангенс, секанс та косеканс). До них належать:

Визначення тригонометричних функций через коло. Відрізки CD та DE позначають версинус та ексеканс відповідно

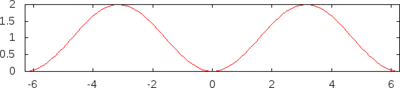
• Синус-верзус (інші назви: версинус, синус версус, також «стрілка дуги»). Визначається як ${\displaystyle \operatorname {versin} \,\vartheta =1-\cos \vartheta =2\sin ^{2}{\frac {\vartheta }{2}}.}$ Деколи позначається як ${\displaystyle \operatorname {vers} \,\vartheta ,\quad \sin \,\operatorname {vers} \,\vartheta .}$

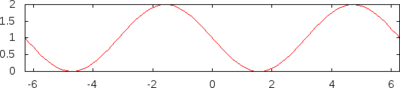
• Косинус-верзус (інші назви: коверсинус, косинус версус). Визначається як ${\displaystyle \operatorname {vercos} \,\vartheta =\operatorname {versin} \,\left({\frac {\pi }{2}}-\vartheta \right)=1-\sin \vartheta .}$ Деколи позначається як ${\displaystyle \operatorname {cvs} \,\vartheta ,\quad \cos \,\operatorname {vers} \,\vartheta .}$

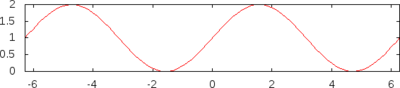
• Гаверсинус (англ. haversinus, скорочення від half the versed sine). Визначається як ${\displaystyle \operatorname {haversin} \,\vartheta ={\frac {\operatorname {versin} \,\vartheta }{2}}=\sin ^{2}{\frac {\vartheta }{2}}.}$ Деколи позначається як ${\displaystyle \operatorname {hav} \,\vartheta .}$

• Ексеканс (англ. exsecant) чи екссеканс. Визначається як ${\displaystyle \operatorname {exsec} \,\vartheta =\sec \vartheta -1.}$

• Екскосеканс: ${\displaystyle \operatorname {excsc} \,\vartheta =\operatorname {exsec} \,\left({\frac {\pi }{2}}-\vartheta \right)=\operatorname {cosec} \,\vartheta -1.}$

${\displaystyle {\textrm {versin}}(\theta ):=2\sin ^{2}\!\left({\frac {\theta }{2}}\right)=1-\cos(\theta )\,}$
${\displaystyle {\textrm {vercosin}}(\theta ):=2\cos ^{2}\!\left({\frac {\theta }{2}}\right)=1+\cos(\theta )\,}$
${\displaystyle {\textrm {coversin}}(\theta ):={\textrm {versin}}\!\left({\frac {\pi }{2}}-\theta \right)=1-\sin(\theta )\,}$
${\displaystyle {\textrm {covercosin}}(\theta ):={\textrm {vercosin}}\!\left({\frac {\pi }{2}}-\theta \right)=1+\sin(\theta )\,}$
${\displaystyle {\textrm {haversin}}(\theta ):={\frac {{\textrm {versin}}(\theta )}{2}}={\frac {1-\cos(\theta )}{2}}\,}$
${\displaystyle {\textrm {havercosin}}(\theta ):={\frac {{\textrm {vercosin}}(\theta )}{2}}={\frac {1+\cos(\theta )}{2}}\,}$
${\displaystyle {\textrm {hacoversin}}(\theta ):={\frac {{\textrm {coversin}}(\theta )}{2}}={\frac {1-\sin(\theta )}{2}}\,}$
${\displaystyle {\textrm {hacovercosin}}(\theta ):={\frac {{\textrm {covercosin}}(\theta )}{2}}={\frac {1+\sin(\theta )}{2}}\,}$

Похідні та інтеграли

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {versin} (x)=\sin {x}}$	${\displaystyle \int \mathrm {versin} (x)\,\mathrm {d} x=x-\sin {x}+C}$
${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {vercosin} (x)=-\sin {x}}$	${\displaystyle \int \mathrm {vercosin} (x)\,\mathrm {d} x=x+\sin {x}+C}$
${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {coversin} (x)=-\cos {x}}$	${\displaystyle \int \mathrm {coversin} (x)\,\mathrm {d} x=x+\cos {x}+C}$
${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {covercosin} (x)=\cos {x}}$	${\displaystyle \int \mathrm {covercosin} (x)\,\mathrm {d} x=x-\cos {x}+C}$
${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {haversin} (x)={\frac {\sin {x}}{2}}}$	${\displaystyle \int \mathrm {haversin} (x)\,\mathrm {d} x={\frac {x-\sin {x}}{2}}+C}$
${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {havercosin} (x)={\frac {-\sin {x}}{2}}}$	${\displaystyle \int \mathrm {havercosin} (x)\,\mathrm {d} x={\frac {x+\sin {x}}{2}}+C}$
${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {hacoversin} (x)={\frac {-\cos {x}}{2}}}$	${\displaystyle \int \mathrm {hacoversin} (x)\,\mathrm {d} x={\frac {x+\cos {x}}{2}}+C}$
${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {hacovercosin} (x)={\frac {\cos {x}}{2}}}$	${\displaystyle \int \mathrm {hacovercosin} (x)\,\mathrm {d} x={\frac {x-\cos {x}}{2}}+C}$

Використання

Версинус, коверсинус та гаверсинус були зручні для логарифмів, оскільки вони всюди невід'ємні, але зараз, за наявності обчислювальної техніки це вже не актуально.

Також використовуються для опису відповідних сигналів в електроніці (наприклад, в функціональних генераторах). Гаверсинус також використовується в розрахунках навігації для уникнення похибок округлення в системах обмеженої розрядності.

Див. також

• Формула гаверсинуса

Джерела

• Статті на сайті Mathworld: эксеканс [Архівовано 29 листопада 2005 у Wayback Machine.], версинус [Архівовано 31 березня 2010 у Wayback Machine.], коверсинус [Архівовано 27 листопада 2005 у Wayback Machine.], гаверсинус [Архівовано 10 березня 2005 у Wayback Machine.].
• Поиск расстояния до точки на карте по координатам.