Довжина кривої

Довжиною кривої в метричному просторі ${\displaystyle (X,\rho )}$ називається варіація відображення, що задає криву, тобто довжина кривої ${\displaystyle \gamma$ :[a,b]\to X}  — це величина, що дорівнює

${\displaystyle \sup \sum \limits _{k=0}^{m}\rho (\gamma (x_{k+1}),\gamma (x_{k})),}$

Полігональне наближення кривої

Довжина кривої
Наступник	площа поверхні
Розмірність	${\displaystyle {\mathsf {L}}}$
Формула	${\displaystyle s=\int _{a}^{b}|{\boldsymbol {c}}'(t)|\,\mathrm {d} t}$
Позначення у формулі	${\displaystyle s}$, ${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x}$, ${\displaystyle |{\boldsymbol {x}}|}$, ${\displaystyle '}$ і ${\displaystyle {\boldsymbol {c}}}$
Символ величини (LaTeX)	${\displaystyle s}$[1]
Властивий	крива
Підтримується Вікіпроєктом	Вікіпедія:Проєкт:Математика
Рекомендована одиниця вимірювання	м[1][2]
Довжина кривої у Вікісховищі

де точна верхня грань береться по всіх розбиттях ${\displaystyle a=x_{0}<x_{1}<\dots <x_{m}=b}$ відрізка ${\displaystyle [a,b]}$.

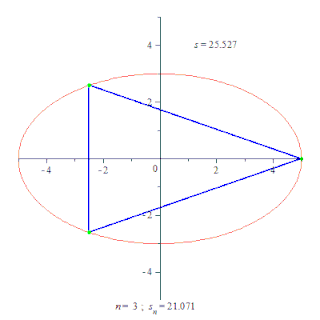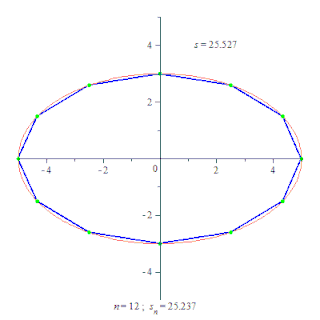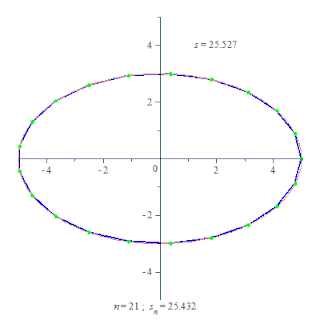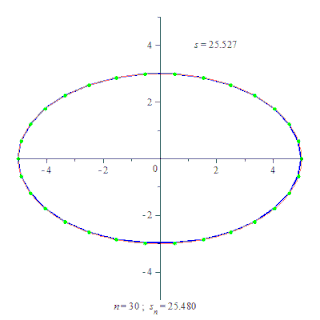
Для евклідового простору це означає, що довжина кривої визначається як точна верхня границя для вписаних в криву ламаних.

Пов'язані визначення

Якщо довжина скінченна, то кажуть, що крива спрямна, інакше — неспрямна.

Формули

Якщо крива класу ${\displaystyle C^{1}}$ в ${\displaystyle \mathbb {R} ^{n}}$, тоді її довжина дорівнює:

• У загальному випадку ${\displaystyle \mathbb {R} ^{n}}$ — ${\displaystyle \int \limits _{a}^{b}{\sqrt {\sum \limits _{k=1}^{n}{f'_{k}}^{2}(t)}}\,dt}$.
• У ${\displaystyle \mathbb {R} ^{3}}$ — ${\displaystyle \int \limits _{a}^{b}{\sqrt {{x'}^{2}(t)+{y'}^{2}(t)+{z'}^{2}(t)}}\,dt}$.
• Якщо крива задана у ${\displaystyle \mathbb {R} ^{2}}$ як ${\displaystyle f(x)}$, то її довжина дорівнює ${\displaystyle \int \limits _{a}^{b}{\sqrt {1+{f'}^{2}(x)}}\,dx}$.
• У полярних координатах для плоскої кривої:

${\displaystyle s=\int _{a}^{b}\limits \!{\sqrt {\rho ^{2}+\left({\frac {d\rho }{d\varphi }}\right)^{2}}}\,d\varphi .}$

Історія

Історично обчислення довжини дуги називалося спрямленням кривої. Задача спрямляння виявилася набагато складнішою, ніж обчислення площі, і в античні часи єдине успішне спрямлення було виконано для кола. Декарт навіть висловлював думку, що «відношення між прямим і кривим невідоме, і навіть, думаю, не може бути пізнане людьми». Першим досягненням стало спрямлення параболи Нейла (1657), виконане Ферма і самим Нейлом. Незабаром було знайдено довжину дуги циклоїди (Рен, Гюйгенс). Грегорі (ще до відкриття математичного аналізу) створив загальну теорію знаходження довжини дуги, яка негайно була використана для різних кривих.

Див. також

• Варіація функції
• Диференціальна геометрія кривих

Література

• Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2025. — 2391 с.(укр.)