Граф Татта

У математичній області теорії графів граф Татта — це 3-регулярний граф з 46 вершинами та 69 ребрами, названий у честь математика Вільяма Татта, що побудував його у 1946 році^[1]. Він має такі характеристики: хроматичне число — 3, хроматичний індекс — 3, обхват — 4, діаметр — 8.

Tutte graph
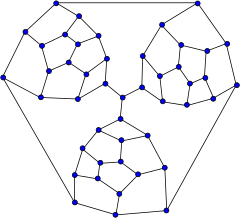Tutte graph
Названо на честь	Вільяма Татта
Вершин	46
Ребер	69
Радіус	5
Діаметр	8
Обхват	4
Автоморфізм	3 (Z/3Z)
Хроматичне число	3
Хроматичний індекс	3
Властивості	Кубічний Планарний Поліедральний

Граф Татта — кубічний багатогранний негамільтоновий граф. Таким чином, він є контрприкладом до гіпотези Тета, що кожен 3-правильний багатогранник має гамільтонів цикл^[2][3]. Опублікований Таттом у 1946 році, це перший контрприклад наведений для цієї гіпотези. Інші контрприклади були знайдені пізніше, у багатьох випадках на основі теореми Грінберга.

Конструкція

Фрагмент Татта

З'єднавши з центральною вершиною три невеликих пласких графа, що звуться фрагментами Татта, вчений, використовуючи теорему Шнейца, побудував негамільтонів багатогранник, що має 25 граней.

«Обов'язкові» ребра фрагмента, які повинні бути частиною гамільтонового шляху через фрагмент, з'єднані в центральній вершині. Оскільки будь-який цикл може використовувати лише два з них, гальмітонового циклу не існує.

Геометрично може бути отриманий з тетраедра (кожна грань якого відповідає чотирьом великим граням з 9 ребрами, три з яких знаходяться між парами фрагментів, а четвертий утворює зовнішню грань) шляхом багаторазового відсікання трьох його вершин.

Алгебраїчна характеристика графа

Група автоморфізмів графа Татта — ${\displaystyle \mathbb {Z} /3\mathbb {Z} }$, циклічна група третього порядку.

Характеристичний многочлен графа Татта:

${\displaystyle (x-3)(x^{15}-22x^{13}+x^{12}+184x^{11}-26x^{10}-731x^{9}+199x^{8}+1383x^{7}-576x^{6}-1061x^{5}+561x^{4}+233x^{3}-151x^{2}+4x+4)^{2}}$

${\displaystyle (x^{15}+3x^{14}-16x^{13}-50x^{12}+94x^{11}+310x^{10}-257x^{9}-893x^{8}+366x^{7}+1218x^{6}-347x^{5}-717x^{4}+236x^{3}+128x^{2}-56x+4).}$

Схожі графи

Хоча Татт створив перший 3-регулярний негамільтоновий граф, він не є найменшим таким графом. У 1965 році Ледербергом був побудований граф Барнетт-Босак-Ледерберга з 38 вершинами^[4][5]. У 1968 році Грінберг побудував додаткові невеликі контрприклади до гіпотези Тета — графи Грінберга на 42, 44 і 46 вершин^[6]. У 1974 році Фолкнер і Янгер опублікували ще два графи — графи Фолкнер-Янгера на 42 і 44 вершини^[7].

Врешті Холтон і Маккей представили ще шість негамільтонових багатогранників із 38 вершинами, для яких пізніше було знайдено три нетривіальні скорочення. Вони утворюються заміною двох вершин п'ятикутної призми тим самим фрагментом, що використовується в прикладі Татта^[8].

Примітки

1. Weisstein, Eric W. Tutte's Graph(англ.) на сайті Wolfram MathWorld.
2. P. G. Tait. Listing's Topologie // Philosophical Magazine (5th ser.). — 1884. — Т. 17. — С. 30–46.. Статья перепечатана в Scientific Papers, Vol. II, pp. 85-98.
3. W. T. Tutte. On Hamiltonian circuits // Journal of the London Mathematical Society. — 1946. — Т. 21, вип. 2. — С. 98–101. — DOI:10.1112/jlms/s1-21.2.98.
4. Lederberg, J. «DENDRAL-64: A System for Computer Construction, Enumeration and Notation of Organic Molecules as Tree Structures and Cyclic Graphs. Part II. Topology of Cyclic Graphs.» Interim Report to the National Aeronautics and Space Administration. Grant NsG 81-60. December 15, 1965. [Архівовано 20 травня 2014 у Wayback Machine.]
5. Weisstein, Eric W. Barnette-Bosák-Lederberg Graph(англ.) на сайті Wolfram MathWorld.
6. Э. Я. Гринберг. Плоские однородные графы степени три без гамильтоновых циклов. // Латв. матем. ежегодник. — Т. 4. — С. 51-58..
7. G. B. Faulkner, D. H. Younger. Non-Hamiltonian Cubic Planar Maps. // Discrete Mathematics. — 1974. — Т. 7. — С. 67-74.
8. D. A. Holton, B. D. McKay. The smallest non-Hamiltonian 3-connected cubic planar graphs have 38 vertices // Journal of Combinatorial Theory, Series B. — 1988. — Т. 45, вип. 3. — С. 305–319. — DOI:10.1016/0095-8956(88)90075-5.