Визначальні рівняння (фізика)

У фізиці визначальні рівняння — це рівняння, які визначають нові величини в термінах базових величин.^[1] У даній статті використовується поточна Міжнародна система величин (ISQ), а не природні чи характеристичні системи.

Опис одиниць вимірювання фізичних величин

Фізичні величини та одиниці дотримуються однакової ієрархії; обрані базові величини мають визначені базові одиниці, з яких можна вивести інші величини й відповідні похідні одиниці.

Аналогія зі змішуванням кольорів

Визначення величин є аналогічним до змішування кольорів і може класифікуватись подібним чином. Основні кольори обираються як базові; за похідні величини обираються вторинні (третинні тощо) кольори. Змішування кольорів є аналогом поєднання величин за допомогою математичних операцій. Але система одиниць може бути різною, наприклад, така як SI (найчастіше), СГСМ, Гаусова, старі імперські одиниці, особлива форма натуральних одиниць.

Вибір базової системи величин і одиниць є довільним, але його треба дотримуватись протягом всього аналізу. Не можна змішувати різні системи одиниць.

У світлі цієї аналогії, основні визначення — це базові величини без визначального рівняння, але з певними стандартизованими умовами, "вторинні" визначення — це величини, визначені виключно з погляду базових величин, "третинні" — величини, визначені з погляду базових і "середніх" величин, "четвертинні" — величини, своєю чергою визначені з погляду базових, "вторинних" і "третинних" величин і так далі.

Мотивація

У фізиці в багатьох моментах необхідні визначення для того, щоб рівняння мали сенс.

Теоретичні аспекти: визначення важливі, оскільки вони вносять ясність в певні розділи фізики. Можна навести приклад  в класичній фізиці. Коли була визначена ентропія, діапазон термодинаміки значно розширився, пов'язавши хаос і безлад з чисельною величиною, яка могла стосуватися енергії й температури, що призводить до розуміння другого закону термодинаміки і статистичної механіки.^[2]

Аналітична зручність: вони дозволяють іншим рівнянням приймати більш компактний запис і тому спрощують математичні маніпуляції шляхом включення параметра у визначенні; входження параметра може бути поглиненим і може бути видаленим з рівняння.^[3]

Простота порівняння: вони дозволяють порівнювати вимірювання, коли вони виявляються двозначними й неясними.

Побудова визначальних рівнянь

Область визначення

Визначальні рівняння зазвичай формулюються у термінах елементарної алгебри та обчислень, векторної алгебри та математичного аналізу, або для найбільш загального застосування тензорної алгебри та обчислень, залежно від рівня навчання і презентації, складності теми й сфери застосування. Більш докладно дану проблему вивчають науковці Львівського національного університету імені Івана Франка. Функції можуть бути включені у визначення, коли це необхідно для обчислень. Величини також можуть бути комплексними, але у природному вимірі актуальна є лише дійсна частина. Часто визначення можуть початись з елементарної алгебри, а потім перейти до векторів, в граничних випадках можуть бути використані обчислення математичного аналізу. Цьому шаблону слідує математика різних рівнів.

Як правило, визначення є явними, тобто визначення величини є предметом рівняння. Іноді рівняння явно не написано, хоча визначення величин може звести рівняння до явного вигляду. Іноді для векторних рівнянь визначені величини у векторному або скалярному добутку не можуть бути знайденими у явному вигляді вектора, але можна обчислити компоненти.

густина потоку енергії F крізь поверхню, dS це похідна векторної області, n  нормаль до поверхні. Для фізичного прикладу, густина струму J чи магнітне поле B будуть F на діаграмі.

Момент імпульсу; скалярні та векторні компоненти.

Приклади

Густина електричного струму — приклад, що охоплює всі ці способи; момент імпульсу — це приклад, який не потребує математичного аналізу.

Елементарна алгебра

Операції просто множення і ділення. Рівняння можуть бути записані в формі добутку або частки, як, зрозуміло, еквівалентно.

	Момент імпульсу	Густина електричного струму
Форма частки	${\displaystyle p={\frac {L}{r}}\,\!}$	${\displaystyle J={\frac {I}{A}}\,\!}$
Форма добутку	${\displaystyle L=pr\,\!}$	${\displaystyle I=JA\,\!}$

Векторна алгебра

Немає ніякого способу, щоб поділити вектор на вектор, немає форми добутку чи частки.

	Момент імпульсу	Густина електричного струму
Форма частки	N/A	${\displaystyle \mathbf {J} \cdot \mathbf {\hat {n}} ={\frac {I}{A}}\,\!}$
Форма добутку	Починаючи з того, що ${\displaystyle L=pr,\,\!}$ оскільки L = 0 коли p і r are паралельні чи перетинаються, найбільше значення, коли перпендикулярні, тому для компоненти p справджується  |p| sin θ, величину кутового моменту L слід записувати: ${\displaystyle L=pr\sin \theta .\,\!}$ ${\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} .\,\!}$	${\displaystyle \mathbf {J} \cdot \mathbf {\hat {n}} A=I,\,\!}$ ${\displaystyle \mathbf {J} \cdot \mathbf {A} =I,\,\!}$

Елементарний математичний аналіз

	Щільність струму
Диференціальна форма	${\displaystyle J=\lim _{A\rightarrow 0}{\frac {I}{A}}={\frac {\mathrm {d} I}{\mathrm {d} A}}\,\!}$
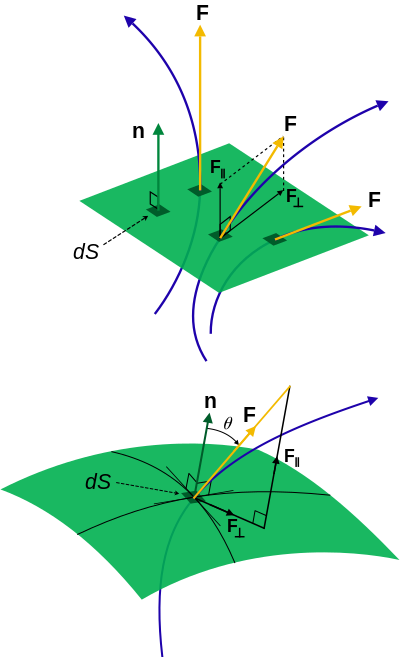
Інтегральна форма	${\displaystyle I=\lim _{A_{i}\rightarrow 0}\sum _{i}JA_{i}=\int _{S}J{\mathrm {d} A}\,\!}$ де dA визначає елемент поверхні (див. поверхневий інтеграл). Альтернатива для інтегральної форми ${\displaystyle \mathrm {d} I=J{\mathrm {d} A},\,\!}$ ${\displaystyle I=\int _{S}J{\mathrm {d} A}.\,\!}$

Арифметичні операції змінюються в граничних випадках диференціації та інтегрування^[4]. Рівняння можуть бути виражені в еквівалентних і альтернативних способах.

Векторне числення

	Щільність струму
Диференціальна форма	${\displaystyle \mathbf {J} \cdot \mathbf {\hat {n}} ={\frac {\mathrm {d} I}{\mathrm {d} A}}\,\!}$
Інтегральна форма	${\displaystyle I=\int _{S}\mathbf {J} \cdot \mathrm {d} \mathbf {A} \,\!}$

Тензорний аналіз

Вектори це тензори першого рангу. Формули нижче це не більше ніж векторні рівняння мовою тензорів.

	Момент імпульсу	Густина електричного струму
Диференціальна форма	N/A	${\displaystyle J_{i}n_{i}={\frac {\mathrm {d} I}{\mathrm {d} A}}\,\!}$
Добуток/Інтегральна форма	починаючи з ${\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} \,\!}$ компонентами  є Li, rj, pi, де i, j, k кожен індекс, що приймає значення 1, 2, 3,  використовуючи тотожність з аналізу тензора ${\displaystyle \mathbf {a} =\mathbf {b} \times \mathbf {c} ,\quad a_{i}=\epsilon _{ijk}b_{j}c_{k},\,\!}$ де εijk це перестановка / тензор Леві-Читинського, призводить до ${\displaystyle L_{i}=\epsilon _{ijk}r_{j}p_{k}.\,\!}$	${\displaystyle J_{i}n_{i}\mathrm {d} A=\mathrm {d} I\,\!}$ ${\displaystyle \int _{S}J_{i}\mathrm {d} A_{i}=I\,\!}$

Прийняття рішень

Іноді є свобода в рамках обраної системи одиниць, щоб визначити одну або більше величин більш ніж одним способом. Ситуація розпадається на два випадки:^[5]

Взаємовиключні визначення: існує кілька можливих варіантів, де величини повинні бути визначені в термінах інших, де може бути використаний тільки один, а не інший. Вибирати більш одного з ексклюзивних рівнянь для визначення веде до протиріччя — одне рівняння може вимагати величину X для визначення, використовуючи іншу величину Y, в той час, як інше рівняння вимагає зворотного, Y визначається за допомогою X. Взаємні суперечності не дають можливості стверджувати, що рівняння визначає якусь величину.

Еквівалентні визначення: визначення рівнянь, які еквівалентні й узгоджені з іншими рівняннями й законами в рамках фізичної теорії, просто написано по-різному.

Є дві можливості для кожного випадку:

Одне визначальне рівняння — одна визначальна величина:  у визначальних рівняннях заведено визначати одну величину з-поміж ряду інших.

Одне визначальне рівняння — ряд визначальних величин: визначальне рівняння використовується для визначення ряду величин з погляду ряду інших. Одне визначальне рівняння не має містити однієї величини, що характеризує всі інші величини в цьому рівнянні, в іншому випадку суперечності виникають знову. Немає визначення певних величин окремо, оскільки вони визначаються в одиничній величині в одному рівнянні.

Протиріччя можна уникнути шляхом визначення величин послідовно; від того, в яких величинах визначено, повинні бути враховані. Приклади, що охоплюють такі екземпляри, зустрічаються в електромагнетизмі.

Диференціальна магнітна сила dF через малий заряд елемента dq  складають  електричний струм,  (звичайний струм використовується). Сила повинна бути лінійно-інтегровною по шляху протікання струму, по відношенню до вектора лінійного об'єкта dr.

Еквівалентні визначення:

Іншим прикладом є індуктивність L, яка має два еквівалентних рівняння, щоб використовувати як визначення.^[6][7]

З погляду I й Φ_B, індуктивність задається

${\displaystyle L=N{\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} I}},\,\!}$

з погляду I й наведеного V

${\displaystyle V=-L{\frac {\mathrm {d} I}{\mathrm {d} t}}.\,\!}$

За законом індукції Фарадея вони є еквівалентними:

${\displaystyle V=-N{\frac {\mathrm {d} \Phi _{B}}{\mathrm {d} t}},\,\!}$

${\displaystyle V{\mathrm {d} t}=-N\mathrm {d} \Phi _{B},\,\!}$

підставляючи в перше визначення для L

${\displaystyle L=-V{\frac {\mathrm {d} t}{\mathrm {d} I}}\,\!}$

${\displaystyle V=-L{\frac {\mathrm {d} I}{\mathrm {d} t}}\,\!}$

і тому вони не є взаємовиключними.

Одне визначальне рівняння — ряд певних величин

Зверніть увагу, що L не можне визначити I й Φ_B одночасно — в цьому немає сенсу. I, Φ_B і V вже, швидше за все, все було визначено раніше (Φ_B наведено вище в рівнянні потоку);

${\displaystyle \mathbf {F} =q\left[\mathbf {E} +\left(\mathbf {v} \times \mathbf {B} \right)\right],\,\!}$

де W = виконана робота на заряду q. Крім того, відсутнє визначення чи I, чи Φ_B окремо — бо L є визначення їх в одному рівнянні.

Однак, з допомогою сили Лоренца для електромагнітного поля:^[8][9][10] як єдине визначальне рівняння для електричного поля Е і магнітного поля B допускається, оскільки Е І Б визначена трьома змінними; сила F, швидкості v і заряд q. Це узгоджується з ізольованим визначення Е і B з Е визначається за допомогою F і q:

${\displaystyle \mathbf {E} =\mathbf {F} /q.\,\!}$

і Б визначаються F, v, і q, як зазначено вище.

Обмеження визначень

Визначення і функції: визначення можуть варіюватись залежно від інших параметрів. Визначальне рівняння визначає тільки як розрахувати точну величину, воно не може описати, як величина змінюється залежно від інших параметрів. Як певна величина змінюється залежно від інших параметрів описується за допомогою рівняння або рівняння, оскільки вона варіюється від одного додатку до іншого і від одного наближення (або спрощення) до іншого.

Визначення та теореми: існує дуже важлива відмінність між визначальними рівняннями й загальним або отриманим результатом, теоремою, законом. Визначальні рівняння взагалі не надають будь-яку інформацію про фізичну систему. Теореми, закони, з іншого боку, не містять значимої інформації, оскільки вони представляють собою розрахунок величини, враховуючи інші властивості системи.

Разові визначення

Деякі рівняння, як правило, є результатом деривації, включають в себе корисні величини, які служать як одноразове визначення в межах своєї сфери застосування.

Див. також

• Рівняння
• Визначальне рівняння (фізична хімія)
• Список рівняння електромагнетизму
• Список рівнянь в класичній механіці
• Список рівнянь механіки рідини
• Список рівняння гравітації
• Список рівнянь в ядерній фізиці та фізиці частинок
• Список рівнянь квантової механіки
• Список рівнянь фотоніки
• Список релятивістських рівнянь
• Таблиця рівнянь термодинаміки

Виноски

1. Warlimont, pp 12–13
2. P.W. Atkins (1978). Physical chemistry (вид. 2nd). Oxford University Press. с. 124–131. ISBN 0-19-855148-7.
3. P.M. Whelan; M.J. Hodgeson (1978). Essential Principles of Physics (вид. 2nd). John Murray. ISBN 0-7195-3382-1.
4. [Архівовано 1 жовтня 2020 у Wayback Machine.], наукова робота ЛНУ.
5. P.M. Whelan; M.J. Hodgeson (1978). Essential Principles of Physics (вид. 2nd). John Murray. с. 6. ISBN 0-7195-3382-1.
6. P.M. Whelan; M.J. Hodgeson (1978). Essential Principles of Physics (вид. 2nd). John Murray. с. 405. ISBN 0-7195-3382-1.
7. I.S. Grant; W.R. Phillips; Manchester Physics (2008). Electromagnetism (вид. 2nd). John Wiley & Sons. с. 231—234. ISBN 978-0-471-92712-9.
8. See, for example, Jackson p 777–8.
9. J.A. Wheeler; C. Misner; K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. с. 72–73. ISBN 0-7167-0344-0.
10. I.S. Grant; W.R. Phillips; Manchester Physics (2008). Electromagnetism (вид. 2nd). John Wiley & Sons. с. 122. ISBN 978-0-471-92712-9.

Джерела

• P.M. Whelan; M.J. Hodgeson (1978). Essential Principles of Physics (вид. 2nd). John Murray. ISBN 0-7195-3382-1.
• G. Woan (2010). The Cambridge Handbook of Physics Formulas. Cambridge University Press. ISBN 978-0-521-57507-2.
• A. Halpern (1988). 3000 Solved Problems in Physics, Schaum Series. Mc Graw Hill. ISBN 978-0-07-025734-4.
• R.G. Lerner; G.L. Trigg (2005). Encyclopaedia of Physics (вид. 2nd). VHC Publishers, Hans Warlimont, Springer. с. 12—13. ISBN 978-0-07-025734-4.
• C.B. Parker (1994). McGraw Hill Encyclopaedia of Physics (вид. 2nd). McGraw Hill. ISBN 0-07-051400-3.
• P.A. Tipler; G. Mosca (2008). Physics for Scientists and Engineers: With Modern Physics (вид. 6th). W.H. Freeman and Co. ISBN 978-1-4292-0265-7.
• L.N. Hand; J.D. Finch (2008). Analytical Mechanics. Cambridge University Press,. ISBN 978-0-521-57572-0.
• T.B. Arkill; C.J. Millar (1974). Mechanics, Vibrations and Waves. John Murray,. ISBN 0-7195-2882-8.
• H.J. Pain (1983). The Physics of Vibrations and Waves (вид. 3rd). John Wiley & Sons,. ISBN 0-471-90182-2.
• J.R. Forshaw; A.G. Smith (2009). Dynamics and Relativity. Wiley,. ISBN 978-0-470-01460-8.
• G.A.G. Bennet (1974). Electricity and Modern Physics (вид. 2nd). Edward Arnold (UK). ISBN 0-7131-2459-8.
• I.S. Grant; W.R. Phillips; Manchester Physics (2008). Electromagnetism (вид. 2nd). John Wiley & Sons. ISBN 978-0-471-92712-9.
• D.J. Griffiths (2007). Introduction to Electrodynamics (вид. 3rd). Pearson Education, Dorling Kindersley,. ISBN 81-7758-293-3.

Для подальшого читання

• L.H. Greenberg (1978). Physics with Modern Applications. Holt-Saunders International W.B. Saunders and Co. ISBN 0-7216-4247-0.
• J.B. Marion; W.F. Hornyak (1984). Principles of Physics. Holt-Saunders International Saunders College. ISBN 4-8337-0195-2.
• A. Beiser (1987). Concepts of Modern Physics (вид. 4th). McGraw-Hill (International). ISBN 0-07-100144-1.
• H.D. Young; R.A. Freedman (2008). University Physics – With Modern Physics (вид. 12th). Addison-Wesley (Pearson International). ISBN 0-321-50130-6.