En İyi Sorular
Zaman Çizelgesi
Sohbet
Bakış Açıları
Matematiksel tablolar
Vikipedi'den, özgür ansiklopediden
Remove ads
Matematiksel tablolar, çeşitli bağımsız değişkenlerle yapılan bir hesaplamanın sonuçlarını gösteren sayı listeleridir. Trigonometrik fonksiyonların tabloları, antik Yunanistan ve Hindistan'da astronomi ve göksel seyir uygulamaları için kullanıldı . Tablolar, hesaplamaları basitleştiren ve büyük ölçüde hızlandıran elektronik hesap makinelerinin fiyatlarının düşerek kolay erişilir hale gelişlerine dek yaygın olarak kullanıldı. Logaritma tabloları ve trigonometrik fonksiyonlar matematik ve fen ders kitaplarında yaygındı ve çok sayıda uygulama için özel tablolar yayınlandı.
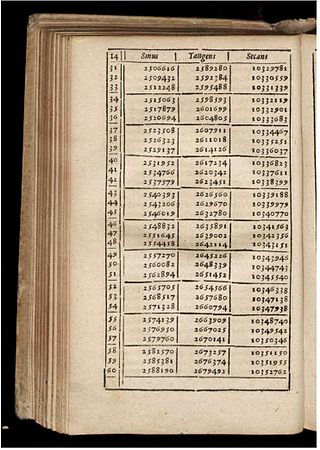
Matthias Bernegger tarafından yazılmış 1619 matematik tabloları kitabından, sinüs, tanjant ve sekant trigonometrik fonksiyonlarının değerlerini gösteren karşılıklı sayfalar. Sol sayfada 45 °'den küçük açılar, sağda 45 °'den büyük açılar bulunur. Kosinüs, kotanjant ve kosekant değerleri karşı sayfadaki değer kullanılarak bulunur.
Remove ads
Tarih ve kullanım
Özetle
Bakış açısı
Bilinen ilk trigonometrik fonksiyon tabloları Hipparchus (c.190 – c.120 BCE) ve Menelaus (c.70-140 CE) tarafından oluşturulmuş ancak ikisi de kaybolmuştur. Günümüze dek ulaşabilen Batlamyus tablosu ile birlikte (c.90 - c.168 CE), bu tabloların üçü de kiriş tablolarıydı, ancak yarım kirişlerden yani sinüs fonksiyonundan değillerdi. Hint matematikçi Āryabhaṭa (476–550 CE) tarafından üretilen tablo, şimdiye kadar yapılmış ilk sinüs tablosu olarak kabul edilir.[1] Āryabhaṭa'nın tablosu, eski Hindistan'ın standart sinüs tablosu olarak kaldı. Bu tablonun doğruluğunu iyileştirmek için sürekli girişimler oldu, bu girişimler Madhava Sangamagrama (c.1350 - c.1425) tarafından sinüs ve kosinüs fonksiyonlarının kuvvet serisi açılımının keşfi ve yedi veya sekiz ondalık basamağa kadar doğru değerlerle sinüs tablosu haline getirilmesiyle sonuçlandı. Adi logaritma tabloları, n'inci köklerin bulunması da dahil olmak üzere, çarpım, bölme ve üs alma işlemlerini hızlı yapmak için bilgisayar ve elektronik hesap makineleri bulunana kadar kullanılmıştır.
Fark makineleri olarak bilinen özel amaçlı mekanik bilgisayarlar, 19. yüzyılda logaritmik fonksiyonların çok terimli yakınsamalarını yani büyük logaritmik tabloları hesaplamak için önerildi. Bu öneri, esas olarak zamanın insan bilgisayarları tarafından yapılan logaritmik tablolardaki hatalardan kaynaklanıyordu. İlk dijital bilgisayarlar II.Dünya Savaşı sırasında kısmen topçu nişanlamaları için özel matematiksel tablolar üretmek amacıyla geliştirildi. 1972'den itibaren, piyasaya sürülen bilimsel hesap makinelerinin artan kullanımıyla matematiksel tabloların çoğu kullanım dışı kaldı.
Bu tür tabloları oluşturmak için son büyük çabalardan biri, 1938'de Works Progress Administration'ın (WPA) bir projesi olarak başlatılan ve yüksek matematik fonksiyonlarını tablo haline getirmek için 450 işsiz katibi kullanan Matematiksel Tablolar Projesi idi. II.Dünya Savaşı boyunca sürdü.[kaynak belirtilmeli] Özel fonksiyonların tabloları hala kullanılmaktadır. Örneğin, normal dağılımın birikimli dağılım fonksiyonunun değerlerini içeren tablo, standart normal dağılım tablosu olarak adlandırılır ve özellikle okullarda yaygın olarak kullanılır. Ancak bilimsel ve grafik hesap makinelerinin kullanımı bu tür tabloları gereksiz hale getirmektedir.
Rastgele erişimli hafızada depolanan tablolar oluşturmak bilgisayar programlamada yaygın bir kod optimizasyon tekniğidir; bu tür tabloların kullanımı, bir tablo aramasının ihtiyaç duyulan hesaplamalardan daha hızlı olduğu durumlarda hesaplamaları hızlandırır. Esasen, tabloları depolamak için gereken bilgisayar bellek alanı ile hesaplama hızı değiş tokuş edilmektedir.
Remove ads
Logaritma tabloları
Özetle
Bakış açısı



Elektronik hesap makinelerinin ve bilgisayarların ortaya çıkmasından önce hesaplamalarda adi logaritmalar (tabanı 10 olan logaritma fonksiyonu) içeren tablolar yaygın olarak kullanılmıştır çünkü logaritmalar çarpma ve bölme sorunlarını çok daha kolay toplama ve çıkarma problemlerine dönüştürür. Onluk logaritmaların benzersiz ve kullanışlı ek bir özelliği bulunur: Birden büyük olan sayıların adi logaritması, yalnızca sadece on üssü ile farklılık gösterir ve mantis olarak bilinen aynı kesirli kısma sahiptir. Genel logaritma tabloları tipik olarak sadece mantisleri içerir; karakteristik olarak bilinen logaritmanın tam sayı kısmı, orijinal sayıdaki rakamları sayarak kolayca belirlenebilir. Benzer bir ilke, 1'den küçük pozitif sayıların logaritmalarının hızlı hesaplanmasına izin verir. Böylece, pozitif ondalık sayıların tamamı için tek bir adi logaritma tablosu kullanılabilir.[2] Karakteristiklerin ve mantislerin kullanımıyla ilgili ayrıntılar için adi logaritmaya bakın.
Tarihçe
1544'te Michael Stifel, logaritmik tablonun erken bir versiyonu olarak kabul edilen 2'nin katları ve tam sayıları tablosunu içeren Arithmetica integra'yı yayınladı.[3][4]
Logaritma yöntemi, 1614 yılında John Napier tarafından Mirifici Logarithmorum Canonis Descriptio (Logaritmanın Harika Kuralının Açıklaması) adlı bir kitapta ortaya atıldı.[5] Kitap, elli yedi sayfa açıklama ve doğal logaritmalarla ilgili doksan sayfa tablo içeriyordu. İngiliz matematikçi Henry Briggs 1615'te Napier'i ziyaret etti ve Napierian logaritmalarını şimdi adi veya 10 tabanında logaritmalar olarak bilinen şekillerini oluşturmak için yeniden ölçeklendirilmesini önerdi. Napier, revize edilmiş tablonun hesaplanmasını Briggs'e devretti. 1617'de, kısa bir logaritma hesabı ve 14. ondalık basamağa göre hesaplanan ilk 1000 tam sayı için bir tablo veren Logarithmorum Chilias Prima'yı ("İlk Bin Logaritma") yayınladılar.
Remove ads
Trigonometrik tablolar
Özetle
Bakış açısı
Trigonometrik hesaplamalar astronominin erken çalışmalarında önemli rol oynadı. Erken dönem tablolar, eskilerden yeni değerleri hesaplamak için trigonometrik ifadelerin (yarım açı ve toplam fark formülleri gibi) tekrar tekrar uygulanmasıyla oluşturuldu.
Basit bir örnek
Yukarıda gösterilen 1619'dan Bernegger tablosu gibi bir trigonometrik fonksiyon tablosunu kullanarak 75 derece, 9 dakika, 50 saniyelik sinüs fonksiyonunu hesaplamak için, değeri 75 derece, 10 dakikaya yuvarlayabilir ve ardından 75 derece sayfasında 10 dakikaya karşılık gelen değeri bulabiliriz, bu değer yukarıda sağda gösterilen 0.9666746'dır.
Ancak, bu yanıt yalnızca dört ondalık basamağa kadar doğrudur. Daha doğru bir sonuç istenirse, aşağıdaki gibi doğrusal olarak interpolasyon yapılabilir:
Bernegger tablosundan:
- sin (75 ° 10 ′) = 0.9666746
- sin (75 ° 9 ′) = 0.9666001
Bu değerler arasındaki fark 0.0000745'.
Bir dakikada 60 saniye olduğundan, (50/60)*0,0000745 ≈ 0,0000621 düzeltmesini elde etmek için farkı 50/60 ile çarparız ve sonra bu sonucu sin (75 ° 9 ′) değerine ekleriz:
- sin (75 ° 9 ′ 50 ″) ≈ sin (75 ° 9 ′) + 0.0000621 = 0.9666001 + 0.0000621 = 0.9666622
Modern bir hesap makinesi sin (75 ° 9 ′ 50 ″) = 0.96666219991 verir, bu nedenle interpolasyonlu cevabımız Bernegger tablosunun 7 basamaklı kesinliği için doğrudur.
Daha yüksek hassasiyete sahip tablolar için (değer başına daha fazla rakam), tam doğruluk elde etmek daha yüksek dereceli interpolasyon gerektirebilir.[6] Elektronik bilgisayarlardan önceki çağda, tablo verilerinin bu şekilde interpolasyonu, seyir, astronomi ve ölçme gibi uygulamalarda gerek duyulan matematiksel fonksiyonlarda yüksek doğruluk elde etmenin tek pratik yoluydu.
Seyir gibi uygulamalarda doğruluğun önemini anlamak için, deniz seviyesinde Dünya'nın ekvatoru boyunca bir dakikalık yay veya bir boylamın (aslında herhangi bir büyük dairenin) yaklaşık bir deniz miline (1.852 kilometre (1.151 mi)) tekabül ettiğini bilmek gerekir.
Ayrıca bakınız
- Abramowitz ve Stegun Matematiksel Fonksiyonlar El Kitabı
- Fark makinesi
- Efemeris
- Grup tablosu
- Logaritma tarihi
- Denizcilik almanağı
- Matris
- Çarpım tablosu
- Rastgele sayı tablosu
- Tablo (bilgi)
- Doğruluk tablosu
- Jurij Vega
Kaynakça
Dış bağlantılar
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads