Graf (matematik)

Matematikte graf ya da çizge, nesne çiftlerinin bir anlamda "ilişkili" olduğu bir dizi nesne kümesini belirleyen bir yapıdır. Nesneler, köşeler (ayrıca düğümler veya noktalar olarak da adlandırılır) adı verilen matematiksel soyutlamalara karşılık gelir ve ilgili düğüm çiftlerinin her birine bir kenar, ayrıt (bağlantı veya çizgi olarak da adlandırılır) adı verilir.^[1] Tipik olarak bir graf, kenarları için çizgiler veya eğriler ile birleştirilen, düğümler için bir nokta veya daire kümesi olarak diyagram şeklinde gösterilir. Graflar ayrık matematikte çalışmanın amaçlarından biridir.

Altı köşeli ve yedi kenarlı bir graf.

Kenarlar yönlü veya yönsüz olabilir. Örneğin, düğümler bir partideki insanları temsil ediyorsa ve iki kişi arasında el sıkışırlarsa bir kenar varsa, o zaman bu grafik yönlendirilmez, çünkü herhangi bir A kişisi B kişisiyle ancak B ile A el sıkışırsa el sıkışabilir. Aksine, eğer bir A kişisinden bir B kişisine herhangi bir kenarı A hayranlığı B'ye karşılık gelirse, o zaman bu graf yönlendirilir, çünkü hayranlık zorunludur. İlk graf türüne yönsüz çizge, sonraki graf türüne yönlü çizge denir.

Çizgeler, graf teorisi tarafından incelenen temel konudur. "Graf" kelimesi ilk olarak bu anlamda 1878'de James Joseph Sylvester tarafından kullanılmıştır.^[2][3]

Tanımlar

Çizge teorisindeki tanımlar değişkendir. Aşağıdakiler, grafları ve ilgili matematiksel yapıları tanımlamanın daha temel yollarından bazılarıdır.

Graf

Üç köşeli ve üç kenarlı bir graf.

Graf (Bazen ayırt etmeye yönelik sınıflandırırken, yönsüz graf ve yönlü graf veya basit graf, katlı graf olarak adlandırılırlar) ^[4][5] bir çift elemandan oluşur G = (V, E), V elemanına köşe denir ve E elemanı kenarlar (bazen bağlantılar veya çizgiler) olarak adlandırılan iki kümeden (iki ayrı öğeye sahip - iki kenar ve bağlayan çizgi- kümeler) oluşan bir dizidir. Her kenar iki ucunda düğüm olacak şekilde tanımlanır.

Bir kenarın {x, y}, düğümleri olan x ve y kenarların uç noktalarıdır. Kenar x ve y'yi ileşkilendirir ve x ve y'yi birbirine bağlar. Bir düğüm herhangi bir kenara ait olmayabilir.

Bir katlı graf, aynı köşe çiftine bitişik çoklu kenarlara izin veren bir genellemedir. Bazı metinlerde katlı graflara basitçe graflar da denir. ^[4][6]

Yönlü çizge

Ana madde: Yönlü çizge

Üç köşeli ve dört yönlendirilmiş kenarlı yönlü bir graf (çift ok her yöndeki bir kenarı temsil eder).

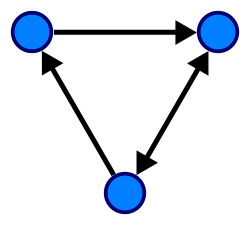
Yönlü graf veya digraf, kenarların oryantasyonlu-yönlendirilmiş olduğu bir graftır.

Karışık graf

Ağırlıklı graf

On köşeli ve on iki kenarlı ağırlıklı bir grafik.

Graf çeşitleri

Yönlendirilmiş graf

Düzenli graf

Tam graf

Sonlu graf

Bağlı graf

İki parçalı graf

Ana madde: İki parçalı graf

Yol graf

Düzlemsel graf

Çember graf

Ağaç

Çoklu ağaç

Gelişmiş sınıflar

Grafların özellikleri

Örnekler

Graf işlemleri

Genellemeler

Ayrıca bakınız

• Kavramsal graf
• Graf (soyut veri türü)
• Graf veritabanı
• Graf çizimi
• Graf teorisi konularının listesi
• Graf teorisi yayınlarının listesi
• Ağ teorisi

Notlar

1. Trudeau, Richard J. (1993). Introduction to Graph Theory (Corrected, enlarged republication. ed.). New York: Dover Pub. s. 19. ISBN 978-0-486-67870-2. 5 Mayıs 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 8 Ağustos 2012. A graph is an object consisting of two sets called its vertex set and its edge set.
2. Bakınız:

   • J. J. Sylvester (7 Şubat 1878) "Chemistry and algebra," 5 Haziran 2020 tarihinde Wayback Machine sitesinde arşivlendi. Nature, 17 : 284. DOI:10.1038/017284a0. 284. sayfadan itibaren: "Every invariant and covariant thus becomes expressible by a graph precisely identical with a Kekuléan diagram or chemicograph."
   • J. J. Sylvester (1878) "On an application of the new atomic theory to the graphical representation of the invariants and covariants of binary quantics, – with three appendices," 5 Haziran 2020 tarihinde Wayback Machine sitesinde arşivlendi. American Journal of Mathematics, Pure and Applied, 1 (1) : 64–90. DOI:10.2307/2369436. JSTOR 2369436. "graf" terimi ilk kez bu yayımda sayfa 65'te geçer.
3. Gross, Jonathan L.; Yellen, Jay (2004). Handbook of graph theory. CRC Press. s. 35. ISBN 978-1-58488-090-5.
4. Bender & Williamson 2010.
5. Bknz: Iyanaga and Kawada, 69 J, s. 234 veya Biggs, s. 4.
6. Graham et al., p. 5.

Kaynakça

• Balakrishnan, V. K. (1997). Graph Theory (1. bas.). McGraw-Hill. ISBN 978-0-07-005489-9.
• Bang-Jensen, J.; Gutin, G. (2000). Digraphs: Theory, Algorithms and Applications. Springer. 26 Ağustos 2011 tarihinde kaynağından arşivlendi. Erişim tarihi: 1 Kasım 2019.
• Bender, Edward A.; Williamson, S. Gill (2010). Lists, Decisions and Graphs. With an Introduction to Probability. 19 Ekim 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 1 Kasım 2019.
• Berge, Claude (1958). Théorie des graphes et ses applications (Fransızca). Paris: Dunod.
• Biggs, Norman (1993). Algebraic Graph Theory (2. bas.). Cambridge University Press. ISBN 978-0-521-45897-9.
• Bollobás, Béla (2002). Modern Graph Theory (1. bas.). Springer. ISBN 978-0-387-98488-9.
• Diestel, Reinhard (2005). Graph Theory (3. bas.). Berlin, New York: Springer-Verlag. ISBN 978-3-540-26183-4. 16 Aralık 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 1 Kasım 2019.
• Graham, R.L.; Grötschel, M.; Lovász, L. (1995). Handbook of Combinatorics. MIT Press. ISBN 978-0-262-07169-7.
• Gross, Jonathan L.; Yellen, Jay (1998). Graph Theory and Its Applications. CRC Press. ISBN 978-0-8493-3982-0.
• Gross, Jonathan L.; Yellen, Jay (2003). Handbook of Graph Theory. CRC. ISBN 978-1-58488-090-5.
• Harary, Frank (1995). Graph Theory. Addison Wesley Publishing Company. ISBN 978-0-201-41033-4.
• Iyanaga, Shôkichi; Kawada, Yukiyosi (1977). Encyclopedic Dictionary of Mathematics. MIT Press. ISBN 978-0-262-09016-2.
• Zwillinger, Daniel (2002). CRC Standard Mathematical Tables and Formulae (31. bas.). Chapman & Hall/CRC. ISBN 978-1-58488-291-6.

Konuyla ilgili yayınlar

• Trudeau, Richard J. (1993). Introduction to Graph Theory (düzeltilmiş, genişletilmiş tekrar bas.). New York: Dover Publications. ISBN 978-0-486-67870-2. 5 Mayıs 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 8 Ağustos 2012.

Dış bağlantılar

• Eric W. Weisstein, Graph (MathWorld)