பெருமம் மற்றும் சிறுமம்

கணிதத்தில் ஒரு சார்பின் பெரும மதிப்பு (maximum value) மற்றும் சிறும மதிப்பு (minimum value) என்பது ஒரு புள்ளியின் அண்மையகத்திலோ அல்லது சார்பின் முழுஆட்களத்திலோ, அச்சார்பு அடையக்கூடிய மிகப்பெரிய அல்லது மிகச் சிறிய மதிப்பாகும். பெரும அல்லது சிறும மதிப்புகள் இரண்டுமே சார்பின் முகட்டு மதிப்புகள் (extreme values) எனப் பொதுவில் அழைக்கப்படுகின்றன.^[1][2][3] பெரும மதிப்பை பெருமம் என்றும் சிறும மதிப்பை சிறுமம் என்றும் சுருக்கமாக அழைப்பது வழக்கம்.

cos(3πx)/x, 0.1≤x≤1.1 சார்பின் இடஞ்சார்ந்த, மீப்பெரு பெருமம் மற்றும் மீச்சிறு சிறுமம்.

பகுமுறை வரையறை

மெய்யெண் கோட்டின்மீது வரையறுக்கப்பட்ட ஒரு மெய்மதிப்புச் சார்பு f -க்கு x^∗ என்ற புள்ளி, இடஞ்சார்ந்த பெருமப்புள்ளி எனில்,

ஏதேனும் ஒரு சிறு மதிப்பு ε > 0 , |x − x^∗| < ε எனும்போது

f(x^∗) ≥ f(x) ஆக அமையும். இப்புள்ளியில் சார்பு அடையும் மதிப்பு அச்சார்பின் இடஞ்சார்ந்த பெரும மதிப்பு அல்லது பெருமம் எனப்படுகிறது.

இதேபோல் x^∗ என்ற புள்ளி இடஞ்சார்ந்த சிறுமப்புள்ளி எனில்,

|x − x^∗| < ε எனும்போது

f(x^∗) ≤ f(x) -ஆக இருக்கும். இப்புள்ளியில் சார்பு அடையும் மதிப்பு அச்சார்பின் இடஞ்சார்ந்த சிறும மதிப்பு அல்லது சிறுமம் எனப்படுகிறது.

x^∗ என்ற புள்ளி சார்பின் மீப்பெரு பெருமப் புள்ளியாக இருக்க அனைத்து x மதிப்பிற்கும்

f(x^∗) ≥ f(x) ஆக இருக்க வேண்டும்.

இதேபோல் x^∗ என்ற புள்ளி சார்பின் மீச்சிறு சிறுமப் புள்ளியாக இருக்க அனைத்து x மதிப்பிற்கும்

f(x^∗) ≤ f(x) ஆக இருக்க வேண்டும்.

கட்டுப்பாடுற்ற ஆட்களம்:

முழு மெய்யெண்கோட்டையும் ஆட்களமாகக் கொண்டிராத சார்புகளுக்கும் பெரும மற்றும் சிறுமம் உண்டு. எந்தவொரு கணத்தையும் ஆட்களமாகக் கொண்ட ஒரு மெய்மதிப்புச் சார்புக்கு மீப்பெரு பெருமம் அல்லது மீச்சிறு சிறுமம் இருக்கலாம். இடஞ்சார்ந்த பெருமம் அல்லது இடஞ்சார்ந்த சிறுமமும் இருக்கலாம். ஆனால் இந்த இடஞ்சார்ந்த பெரும அல்லது சிறுமப் புள்ளிகளின் அண்மையகங்கள் அச்சார்பின் ஆட்களத்தினுள் கண்டிப்பாக அமைய வேண்டும். அண்மையகம் என்பது |x − x^∗| < ε என அமையும் x மதிப்புகள் கொண்ட கணம்.

ஒரு தொடர்ச்சியான மெய்மதிப்புச் சார்பு இறுக்கமான கணத்தில் (compact set) வரையறுக்கப்பட்டிருந்தால் அச்சார்புக்கு பெரும மற்றும் சிறுமப் புள்ளிகள் அக்கணத்திலேயே அமையும். மெய்யெண் கோட்டின் மீது அமையும் ஓர் மூடிய இடைவெளியில் வரையறுக்கப்பட்ட ஒரு மெய்மதிப்புச் சார்பு இதற்கு எடுத்துக்காட்டாகும்.(மேலே தரப்பட்ட படம்). அண்மையகத்தின் வரையறைப்படி ஓர் இடைவெளியின் இறுதி முனைப்புள்ளிகள் இடஞ்சார்ந்த பெரும அல்லது சிறுமப் புள்ளிகளாக அமைவதற்கு வாய்ப்பில்லை. எனவே முடிவுறு ஆட்களம் கொண்ட சார்பின் மீப்பெரு பெருமம் அல்லது மீச்சிறு சிறுமமானது, இடஞ்சார்ந்த பெருமம் அல்லது இடஞ்சார்ந்த சிறுமமாக இருக்கலாம் அல்லது இல்லாமலும் இருக்கலாம்.

சார்புகளின் பெருமம் மற்றும் குறுமம் காணல்

முகட்டு மதிப்புத் தேற்றத்தின்படி, ஒரு மூடிய இடைவெளியில் வரையறுக்கப்பட்ட மெய்மதிப்புச் சார்பு தொடர்ச்சியான சார்பு எனில் அதற்கு கண்டிப்பாக மீப்பெரு பெருமம் மற்றும் மீச்சிறு சிறுமம் உண்டு. மேலும் இந்த மீப்பெரு பெருமம் அல்லது மீச்சிறு சிறுமம், சார்பின் ஆட்களத்துள் அல்லது இடைவெளியின் முடிவுப் புள்ளிகளில் அமையும் இடஞ்சார்ந்த பெருமம் அல்லது இடஞ்சார்ந்த சிறுமமாக அமையும். மீப்பெரு பெருமம் அல்லது மீச்சிறு சிறுமம் காண:

• முதலில் சார்பின் ஆட்களத்துக்குள் அமையும் இடஞ்சார்ந்த பெருமம், இடஞ்சார்ந்த சிறுமம், இடைவெளியின் முனைகளில் அமையும் பெருமம், சிறுமம் அனைத்தையும் கண்டுபிடித்துக் கொள்ள வேண்டும்.
• பின் அவற்றுள் மிகப்பெரிய மதிப்பைத் தேர்ந்தெடுத்தால், அது மீப்பெரு பெருமமாகவும் மிகச் சிறிய மதிப்பைத் தேட்ந்தெடுக்க அது, மீச்சிறு சிறுமமாகவும் அமையும்.

இடஞ்சார்ந்த பெருமம்(சிறுமம்) காணல்:

• ஃபெர்மா தேற்றத்தின்படி, ஒரு சார்பின் இடஞ்சார்ந்த பெருமம்(சிறுமம்) அச்சார்பின் மாறுநிலைப்புள்ளிகளில் அமையும்.
• முதலில் சார்பின் மாறுநிலைப் புள்ளிகளைக் காணவேண்டும்.
• பின் ஒரு மாறுநிலைப் புள்ளி இடஞ்சார்ந்த பெருமப்புள்ளியா அல்லது இடஞ்சார்ந்த சிறுமப்புள்ளியா என்ற வித்தியாசத்தை முதல் வகைக்கெழுச் சோதனை அல்லது இரண்டாம் வகைக்கெழுச் சோதனையை பயன்படுத்திக் காண வேண்டும்.

தனித்தனி துண்டுகளாக ஒரு சார்பு வரையறுக்கப்பட்டிருந்தால் முதலில் ஒவ்வொரு துண்டிற்கும் தனித்தனியாக பெருமம் மற்றும் சிறுமம் கண்டுபிடித்துப் பின்னர் அவற்றுள் மிகப் பெரிய மற்றும் மிகச் சிறிய மதிப்புகளை மீப்பெரு பெருமமாகவும் மீச்சிறு சிறுமமாகவும் கொள்ளல் வேண்டும்.

எடுத்துக்காட்டுகள்

${\displaystyle {\sqrt[{x}]{x}}}$ சார்புக்கு x = e -ல் மீப்பெரு பெருமம்.படம் 2

${\displaystyle f(x)=x^{3},\,}$ சார்பின் வரைபடம். வளவுமாற்றுப் புள்ளி (0,0). படம் 3

• ${\displaystyle f(x)=x^{2},\,}$ -சார்புக்கு:

ஒரேயொரு மீச்சிறு சிறுமம் x = 0 -ல் அமையும்.

• ${\displaystyle f(x)=x^{3},\,}$ -சார்புக்கு:

x = 0 -ல் முதல் வகைக்கெழு (3x²) = 0

எனினும் இப்புள்ளி மீப்பெரு பெரும மற்றும் மீச்சிறு சிறுமப் புள்ளி அல்ல.

x = 0 என்ற புள்ளி, இச்சார்பின் வளைவுமாற்றுப் புள்ளி.(படம் 3)

• ${\displaystyle {\sqrt[{x}]{x}}}$ -சார்புக்கு:

x = e என்ற புள்ளியில் ஒரேயொரு மீப்பெரு பெருமம் உண்டு. (படம் 2.)

• ${\displaystyle f(x)={\frac {1}{x^{x}}},\,}$ சார்புக்கு:

x = 1/e புள்ளியில் ஒரேயொரு மீப்பெரு பெருமம் உண்டு.

•  :${\displaystyle f(x)={\frac {x^{3}}{3}}-x,\,}$ சார்புக்கு:

முதல் வகைக்கெழு x² − 1,

இரண்டாம் வகைக்கெழு 2x.

முதல் வகைக்கெழுவை பூச்சியத்துக்குச் சமப்படுத்த மாறுநிலைப் புள்ளிகள் x = −1 மற்றும் +1 கிடைக்கும்.

இரண்டாம் வகைக்கெழுவின் குறியிலிருந்து, x = −1 என்பது இடஞ்சார்ந்த பெருமப்புள்ளி என்றும்

x = 1 என்பது இடஞ்சார்ந்த சிறுமப்புள்ளி என்றும் காணலாம்.

இச்சார்புக்கு மீப்பெரு பெருமம் மற்றும் மீச்சிறு சிறுமம் கிடையாது.

• ${\displaystyle f(x)=|x|,\,}$ சார்புக்கு:

x = 0 புள்ளியில் மீப்பெரு பெருமம் உண்டு.

ஆனால் சார்பை x = 0 புள்ளியில் வகையிட முடியாது என்பதால் இப்பெருமத்தை வகையிடல் மூலம் காண முடியாது.

• ${\displaystyle f(x)=cos(x),\,}$ சார்புக்கு:

முடிவிலா எண்ணிக்கையிலான மீப்பெரு பெரும மதிப்புகள், x = 0, ±2π, ±4π, …, புள்ளிகளிலும்;

மீச்சிறு சிறும மதிப்புகள் x = ±π, ±3π, …., புள்ளிகளிலும் உள்ளன.

• ${\displaystyle f(x)=2cos(x)-x,\,}$ சார்புக்கு:

முடிவிலா எண்ணிக்கையிலான இடஞ்சார்ந்த பெரும மற்றும் சிறும மதிப்புகள் உண்டு.

ஆனால் மீப்பெரு பெரும மற்றும் மீச்சிறு சிறும மதிப்புகள் கிடையாது.

• ${\displaystyle f(x)={\frac {cos3\pi x}{x}},\,}$; 0.1 ≤ x ≤ 1.1 சார்புக்கு:

x = 0.1 (முனைப்புள்ளி) -மீப்பெரு பெருமம்,

x = 0.3 க்கு அருகில் மீச்சிறு சிறுமம்,

x = 0.6 -க்கு அருகில் இடஞ்சார்ந்த பெருமம்,

x = 1.0. -க்கு அருகில் இடஞ்சார்ந்த சிறுமம் உள்ளது.(முதல் படத்தைப் பார்க்க.)

• ${\displaystyle f(x)=x^{3}+3x^{2}-2x+1,\,}$ என்ற சார்பு வரையறுக்கப்படும் இடைவெளி [−4,2]:

x = −1−^√15⁄₃ இடஞ்சார்ந்த பெருமம்,

x = −1+^√15⁄₃ இடஞ்சார்ந்த சிறுமம்,

x = 2 மீப்பெரு பெருமம்

x = −4 மீச்சிறு சிறுமம்.

ஒன்றுக்கு மேற்பட்ட மாறிகளில் அமைந்த சார்புகள்

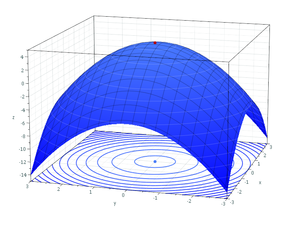
ஒரு மாறியில் அமைந்த சார்புகளுக்குரிய பெரும மற்றும் சிறும மதிப்புகளிக்கான நிபந்தனைகள், ஒன்றுக்கும் மேற்பட்ட மாறிகளில் அமைந்த சார்புகளுக்கும் பொருந்தும்.

ஒன்றுக்கும் மேற்பட்ட மாறிகளில் அமைந்த சார்பின் இடஞ்சார்ந்த பெருமத்திற்குத்(சிறுமம்) தேவையான நிபந்தனைகள்:

• பெரும அல்லது சிறும மதிப்பு காண வேண்டிய சார்பின் முதலாம் பகுதிவகைக்கெழுக்கள் பூச்சியமாகவும்
• இரண்டாம் பகுதிவகைக்கெழு எதிர்மமாகவும்(நேர்மம்) இருக்க வேண்டும்

சேணப்புள்ளியாக அமைவதற்கான சாத்தியமும் உள்ளதால் இந்நிபந்தனைகள் தேவையான நிபந்தனைகள் மட்டுமாகவே அமையும். ஆனால் இவை போதுமான நிபந்தனைகள் அல்ல. மேலும் சார்பானது, அதன் ஆட்களம் முழுவதிலும் வகையிடத்தக்கதாக இருக்க வேண்டும். இரண்டாம் வகைக்கெழு சோதனை மூலம் மாறுநிலைப் புள்ளிகள் பெருமமா அல்லது சிறுமமா என்ற வேறுபாட்டை அறியலாம்.

மாறாக மீப்பெரு பெருமம் அல்லது மீச்சிறு சிறுமம் காண்பதில் ஒரு மாறியில் அமைந்த சார்புகளுக்கும் ஒன்றுக்கு மேற்பட்ட மாறியில் அமைந்த சார்புகளுக்கும் இடையே வேறுபாடு உள்ளது.

மெய்யெண் கோட்டின் ஒரு மூடிய இடைவெளியில் வரையறுக்கப்பட்ட எல்லைக்குட்பட்ட வகையிடத்தக்க ஒரு சார்புக்கு இடஞ்சார்ந்த சிறுமமாக அமையும் ஒரேயொரு மாறுநிலைப் புள்ளியிருக்குமானால் அதுவே மீச்சிறு சிறுமப் புள்ளியாகவும் அமையும்.

ஆனால் இரண்டு அல்லது இரண்டுக்கு மேற்பட்ட மாறிகளில் அமைந்த சார்புகளுக்கு இது பொருந்தாது.

${\displaystyle f(x,y)=x^{2}+y^{2}(1-x)^{3},\qquad x,y\in \mathbb {R} ,}$ என்ற சார்புக்கு:

ஒரேயொரு மாறுநிலைப் புள்ளி (0,0).

இது இடஞ்சார்ந்த சிறுமப் புள்ளியாகவும் அமையும். ƒ(0,0) = 0.

ஆனால் இப்புள்ளி மீச்சிறு சிறுமப்புள்ளி கிடையாது. ஏனென்றால் ƒ(4,1) = −11 என  0-ஐ விடக் குறைவான மதிப்பு சார்புக்கு உள்ளது.

மீப்பெரு பெருமப் புள்ளி.

எதிர் எடுத்துக்காட்டு

மேற்கோள்கள்

1. Stewart, James (2008). Calculus: Early Transcendentals (6th ed.). Brooks/Cole. பன்னாட்டுத் தரப்புத்தக எண் 0-495-01166-5.
2. Larson, Ron; Edwards, Bruce H. (2009). Calculus (9th ed.). Brooks/Cole. பன்னாட்டுத் தரப்புத்தக எண் 0-547-16702-4.
3. Thomas, George B.; Weir, Maurice D.; Hass, Joel (2010). Thomas' Calculus: Early Transcendentals (12th ed.). Addison-Wesley. பன்னாட்டுத் தரப்புத்தக எண் 0-321-58876-2.

வெளி இணைப்புகள்

• Maxima and Minima From MathWorld—A Wolfram Web Resource.
• Thomas Simpson's work on Maxima and Minimaat
• Application of Maxima and Minima with sub pages of solved problems