சாய்வு

ஒரு நேர்கோடு எப்படி சாய்ந்துள்ளது அல்லது சரிந்துள்ளது என்றதன் அளவே சாய்வு (slope) எனப் பொதுவாக அழைக்கப்படும்^[1]. சாய்வை ஏற்றம்/ஓட்டம் அல்லது இறக்கம்/ஓட்டம் என்று வரையறுக்கலாம். சாய்வின் அளவு அதிகமானால் அதன் சரிவு அதிகமாய் உள்ளதை குறிக்கும். பொதுவாக சாய்வு m எனக் குறிக்கப்படுகிறது^[2].

• ஒரு கோட்டின் திசையானது கூடுவதாக, குறைவதாக, கிடைமட்டமானதாக அல்லது செங்குத்தானதாக ஒரு கோட்டின் திசை இருக்கும்.
  • ஒரு கோடு இடப்புறமிருந்து வலப்புறமாக மேல் நோக்கிச் செல்லுமானால் அது கூடும் கோடு. அக்கோட்டின் சாய்வு நேர் மதிப்பாக இருக்கும் ( ${\displaystyle m>0}$).
  • ஒரு கோடு இடப்புறமிருந்து வலப்புறமாக கீழ் நோக்கிச் செல்லுமானால் அது குறையும் கோடு. அக்கோட்டின் சாய்வு எதிர் மதிப்பாக இருக்கும் (${\displaystyle m<0}$).
  • ஒரு கோடு கிடைமட்டமாக இருந்தால் அதன் சாய்வின் மதிப்பு பூச்சியம் (${\displaystyle m=0}$). இது ஒரு மாறிலிச் சார்பு.
  • ஒரு கோடு செங்குத்தாக இருந்தால் அதன் சாய்வின் மதிப்பு வரையறுக்கப்படாதது ஆகும் (${\displaystyle m}$ = வரையறுக்கப்படவில்லை).
• ஒரு கோட்டின் சாய்வின் தனிமதிப்பால் அக்கோட்டின் செங்குத்து நிலை, சரிவு நிலை அளவிடப்படுகிறது.

${\displaystyle m=\Delta y/\Delta x.}$

வரையறை

Slope illustrated for y = (3/2)x − 1. Click on to enlarge

ஆள்கூற்று முறைமையில், f(x)=-12x+2 லிருந்து f(x)=12x+2 வரை ஒரு நேர்கோட்டின் சாய்வு

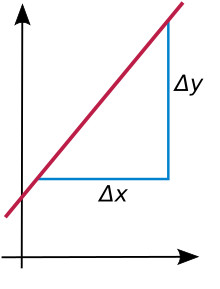
x , y அச்சுக்களைக் கொண்ட தளத்திலமைந்த ஒரு கோட்டின் சாய்வின் குறியீடு m . அக்கோட்டின் மீதமைந்த இரு வெவ்வேறான புள்ளிகளின் y அச்சுச் தூரங்களின் வித்தியாசத்திற்கும் ஒத்த x அச்சுத் தூரங்களின் வித்தியாசத்திற்குமான விகிதமே அக்கோட்டின் சாய்வு. இச் சாய்விற்கான கணித வாய்ப்பாடு:

${\displaystyle m={\frac {\Delta y}{\Delta x}}={\frac {\text{rise}}{\text{run}}}.}$ = ஏற்றம்/ஓட்டம்

(கணிதத்தில் வித்தியாசம் அல்லது மாற்றத்தைக் குறிப்பதற்குப் பொதுவாக கிரேக்க எழுத்து Δ பயன்படுத்தப்படுகிறது.)

(x₁,y₁), (x₂,y₂) என்பன கோட்டின் மீதமைந்த இரு புள்ளிகள் எனில்,

x இல் ஏற்படும் மாற்றம் = x₂ − x₁ (ஓட்டம்),

y இல் ஏற்படும் மாற்றம் = y₂ − y₁ (ஏற்றம்).

சாய்வு காணும் வாய்ப்பாடு:

${\displaystyle m={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}.}$

xy தளத்திலுள்ள செங்குத்துக் கோடுகளுக்கு (y அச்சுக்கு இணையான கோடுகள்) இவ்வாய்ப்பாட்டினைப் பயன்படுத்த இயலாது. ஏனென்றால் அக்கோடுகளின் மீதுள்ள எல்லாப்புள்ளிகளுக்கும் x அச்சு தூரங்கள் சமம். சாய்வின் வாய்ப்பாட்டின் பகுதியின் மதிப்பு பூச்சியமாவதால் பின்னத்தின் மதிப்பைக் கணக்கிட முடியாது. எனவே செங்குத்துக்கோடுகளின் சாய்வின் மதிப்பு முடிவிலி, அதாவது வரையறுக்கப்படாதது ஆகும்.

எடுத்துக்காட்டுகள்

• P = (1, 2), Q = (13, 8) என்ற இரு புள்ளிகள் வழியே ஒரு கோடு செல்கிறது எனில் அக்கோட்டின் சாய்வு:

${\displaystyle m={\frac {\Delta y}{\Delta x}}={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}={\frac {8-2}{13-1}}={\frac {6}{12}}={\frac {1}{2}}}$.

சாய்வு நேர் எண்ணாக இருப்பதால் கோட்டின் திசை கூடும்போக்குடையது. மேலும் சாய்வின் தனிமதிப்பு ஒன்றைவிடக் குறைவாக இருப்பதால் (|m|&<1) கோடு அதிக செங்குத்தாக இருக்காது, அதன் சாய்வுகோணம் <45° ஆக இருக்கும்

• (4, 15), (3, 21) என்ற இரு புள்ளிகள் வழியே செல்லும் கோட்டின் சாய்வு:

${\displaystyle m={\frac {21-15}{3-4}}={\frac {6}{-1}}=-6.}$

சாய்வு எதிர் எண்ணாக இருப்பதால் கோட்டின் திசை குறையும் போக்குடையது. |m|>1 என்பதால் கோட்டின் இறக்கம் அதிகமானதாக இருக்கும். (சாய்வு கோணம் >45°).

இயற்கணிதமும் வடிவவியலும்

• x இல் அமைந்த நேரியல் சார்பு y எனில், சார்பின் வரைபடம் ஒரு கோடு. அக்கோட்டின் சாய்வு, சார்பின் சமன்பாட்டிலுள்ள x இன் கெழுவாக இருக்கும். எனவே ஒரு நேர்கோட்டின் சமன்பாடு ${\displaystyle y=mx+b\,}$ எனில் அக்கோட்டின் சாய்வு m. கோட்டின் இச்சமன்பாட்டு வடிவம் சாய்வு-வெட்டுத்துண்டு வடிவம் எனப்படும். கோடானது y-அச்சில் உண்டாக்கும் வெட்டுத்துண்டின் அளவு b.
• சாய்வு m கொண்ட ஒரு கோட்டின் மீதுள்ள ஒரு புள்ளி (x₁,y₁) எனில் அக்கோட்டின் சமன்பாடு:

${\displaystyle y-y_{1}=m(x-x_{1}).\!}$ (புள்ளி-சாய்வு வடிவச் சமன்பாடு)

${\displaystyle ax+by+c=0\,}$ என்ற நேரியல் சமன்பாடு குறிக்கும் கோட்டின் சாய்வு:

${\displaystyle -{\frac {a}{b}}\;}$.

• இரு கோடுகளின் சாய்வுகள் சமமாக இருந்தால், இருந்தால் மட்டுமே, அக்கோடுகள் இரண்டும் ஒன்றுக்கொன்று இணையானவை. (கோடுகள் இரண்டும் ஒன்றோடொன்று பொருந்தாக் கோடுகளாக இருக்க வேண்டும்)
• இரு கோடுகளின் சாய்வுகளின் பெருக்குத்தொகையின் மதிப்பு  −1 எனில் அக்கோடுகள் இரண்டும் ஒன்றுக்கொன்று செங்குத்தானவை.
• ஒரு கோடு நேர் x-அச்சுடன் உண்டாக்கும் கோணம் (கோட்டின் சாய்வுகோணம்) θ (-90° , 90° இரண்டுக்கும் இடைப்பட்ட அளவு கொண்டது) எனில் அக்கோட்டின் சாய்வு:

${\displaystyle m=\tan(\theta )}$

${\displaystyle \theta =\arctan(m)}$

எடுத்துக்காட்டுகள்

(2,8), (3,20) என்ற இரு புள்ளிகள் வழியாகச் செல்லும் கோட்டின் சாய்வு:

${\displaystyle {\frac {(20-8)}{(3-2)}}\;=12.\,}$

எனவே கோட்டின் சமன்பாடு புள்ளி-சாய்வு வடிவில்:

${\displaystyle y-8=12(x-2)=12x-24\,}$

${\displaystyle y=12x-16.\,}$

இக்கோடு x அச்சுடன் உண்டாக்கும் கோணம் θ எனில்:

${\displaystyle \theta =\arctan(12)\approx 85.2^{\circ }\,.}$

y = -3x + 1, y = -3 x - 2 என்ற இரு கோடுகளின் சாய்வுகள் சமமாக (m = -3) உள்ளன. மேலும் அவையிரண்டும் ஒன்றோடொன்று பொருந்தும் கோடுகளும் அல்ல என்பதால், இரண்டும் ஒன்றுக்கொன்று இணைகோடுகள்.

y = -3x + 1 கோட்டின் சாய்வு m₁ = -3

y = ^x/₃ - 2 கோட்டின் சாய்வு m₂ = ¹/₃

இரண்டின் சாய்வுகளின் பெருக்குத்தொகை -1. எனவே இரண்டும் ஒன்றுக்கொன்று செங்குத்து.

நுண்கணிதம்

வளைகோட்டின் மீதுள்ள ஒவ்வொரு புள்ளியிலும் வளைகோட்டிற்கு வரையப்படும் தொடுகோட்டின் சாய்வுக்குச் சமமாக, அப்புள்ளியில் காணப்படும் வகைக்கெழு உள்ளது. குறிப்பு: புள்ளியிடப்பட்ட பச்சை நிறக் கோடாகத் தொடுகோடு உள்ளபோது வகைக்கெழு நேர் எண்ணாகவும், புள்ளியிடப்பட்ட சிவப்பு நிறக் கோடாகத் தொடுகோடு உள்ளபோது வகைக்கெழு எதிர் எண்ணாகவும், கருப்பு நிற அழுத்தமான கோடாக தொடுகோடு உள்ள இடங்களில் சாய்வு பூச்சியமாகவும் உள்ளதைக் காணலாம்.

வகை நுண்கணிதத்தில் சாய்வு முக்கியமான ஒரு கருத்துரு. நேரியலற்ற சார்புகளுக்கு அதன் மாறுவீதம் வளைகோட்டின் மீது மாறுபடுகிறது. ஒரு வளைகோட்டின் மீதமையும் ஒரு புள்ளியில் காணப்படும் வகைக்கெழுவானது, அப்புள்ளியில் வளைகோட்டிற்கு வரைப்படும் தொடுகோட்டின் சாய்விற்குச் சமம். எனவே ஒரு வளைகோட்டின் மீதமையும் ஒரு புள்ளியில் காணப்படும் வகைக்கெழு, அப்புள்ளியில் வளைக்கோட்டுச் சார்பின் மாறுவீதமாகும்.

வளைகோட்டின் மீதுள்ள இரு புள்ளிகளுக்கு இடைப்பட்ட x , y -அச்சுக்களின் வழியான தூரங்கள் முறையே Δx , Δy எனில் அவ்விரு புள்ளிகளை இணைக்கும் வெட்டுக்கோட்டின் சாய்வு:

${\displaystyle m={\frac {\Delta y}{\Delta x}}}$,

(ஒரு கோட்டின் மீதமையும் இரு புள்ளிகளுக்கு இடைப்பட்ட வெட்டுக்கோடு எடுத்துக்கொள்ளப்பட்ட மூலக்கோடாகவே இருக்கும். ஆனால் வேறு எந்தவகை வளைகோடுகளுக்கும் அவ்வாறு அமையாது.)

எடுத்துக்காட்டாக, y = x² என்ற வளையின் புள்ளிகள் (0,0) , (3,9) இரண்டையும் இணைக்கும் வெட்டுக்கோட்டின் சாய்வு 3. இடைமதிப்புத் தேற்றப்படி, இவ்வளைகோட்டிற்கு x = ³⁄₂ புள்ளியில் தொடுகோட்டின் சாய்வும் 3.)

Δy , Δx இன் அளவுகள் பூச்சியத்தை அணுகுமாறு, இரு புள்ளிகளையும் ஒன்று மற்றொன்றை நெருங்குமாறு நகர்த்தும்போது வெட்டுக்கோடு கிட்டத்தட்ட ஒரு தொடுகோடாக மாறும். எனவே அந்நிலையில் வெட்டுக்கோட்டின் சாய்வும் தொடுகோட்டின் சாய்வை அணுகும். வகை நுண்கணிதத்தைப் பயன்படுத்தி Δy , Δx இன் மதிப்புகள் 0 ஐ அணுகும்போது Δy/Δx எல்லை மதிப்பைக் காணலாம். இந்த எல்லையின் மதிப்பே தொடுகோட்டின் சாய்வு. y இன் மதிப்பு x ஐச் சார்ந்தது எனில், Δx மட்டும் 0 ஐ அணுகுவதாகக் கொண்டு Δy/Δx இன் எல்லை மதிப்பைக் கணக்கிட்டால் போதுமானது. எனவே Δx பூச்சியத்தை அணுகும்போதான Δy/Δx இன் எல்லை மதிப்பு தொடுகோட்டின் சாய்வு ஆகும். வகையிடல் எனப்படும் இவ்வெல்லை மதிப்பு dy/dx எனக் குறிக்கப்படுகிறது.

${\displaystyle {\frac {dy}{dx}}=\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}}$

மேற்கோள்கள்

1. Clapham, C.; Nicholson, J. (2009). "Oxford Concise Dictionary of Mathematics, Gradient" (PDF). Addison-Wesley. p. 348. பார்க்கப்பட்ட நாள் September 2013. {{cite web}}: Check date values in: |accessdate= (help)
2. Weisstein, Eric W. "Slope". MathWorld--A Wolfram Web Resource. பார்க்கப்பட்ட நாள் September 2013. {{cite web}}: Check date values in: |accessdate= (help)