From Wikipedia, the free encyclopedia
இரு வடிவவியல் வடிவங்கள் வடிவமைப்பிலும் அளவிலும் சமமானவையாக இருந்தால் அவை சர்வசமம் அல்லது முற்றொப்பு (Congruence) ஆனவை எனப்படுகின்றன. அதாவது சர்வசமமான இரு வடிவங்களும், ஒன்று மற்றதன் கண்ணாடி எதிருரு போல அமைந்திருக்கும்.[1] இரண்டு புள்ளிகளின் கணங்களில், ஒன்றை மற்றதாக உருமாற்றக்கூடிய சமஅளவை உருமாற்றம் "இருந்தால், இருந்தால் மட்டுமே", அவையிரண்டும் சர்வசமமானவையாக இருக்க முடியும். அதாவது சர்வசமமான இரு வடிவங்களில், ஒரு வடிவத்தை அதன் அளவில் மாற்றமில்லாமல் எதிரொளிப்பு, இடப்பெயர்ச்சி, சுழற்சி மூலமாக மற்ற வடிவத்தோடு துல்லியமாக ஒன்றச் செய்யமுடியும். ஒரு வரைதாளில் இரு வெவ்வேறு இடங்களில் வரையப்பட்டுள்ள இரு வடிவங்கள் சர்வசமமானவை எனில் அவை இரண்டையும் அத்தாளிலிருந்து வெட்டி எடுத்து ஒன்றின்மேல் மற்றொன்றை மிகச்சரியாகப் பொருத்த முடியும்.

அடிப்படை வடியவியலில் "சர்வசமம்" என்பது பின்வருமாறு அமையும்[2]:

இரு பல்கோணிகள் சர்வசமமாக இருக்கவேண்டுமானால் முதற்கட்டமாக, அவற்றின் பக்கங்களின் எண்ணிகை சமமாய் இருக்க வேண்டும். சம எண்ணிகையிலான பக்கங்கள் கொண்ட இரு பல்கோணிகளைச் சர்வசமமானவையா எனக் கண்டறிய கீழுள்ள முறையில் சர்வசமமானவையா எனக் கண்டறியலாம்:
இம்முறைகளால் எந்தவொரு நிலையிலும் இரு பல்கோணிகளையும் ஒன்றுடனொன்று பொருத்த முடியாமல் போனால் அவ்விரு பல்கோணிகளும் சர்வசமமற்றவை.
இரு முக்கோணங்களின் ஒத்த பக்கங்கள் சம அளவானவையாகவும், ஒத்த கோணங்கள் சம அளவானவையாகவும் இருந்தால், அவ்விரு முக்கோணங்களும் சர்வசமமானவை ஆக இருக்கும். முக்கோணம், முக்கோணம் DEF முக்கோணத்துடன் முக்கோணம் ABC சர்வசமமானது என்பதைக் குறிக்கும் குறியீடு:
இரு முக்கோணங்கள் சர்வசமமானவையா என்பதைத் தீர்மானிப்பதற்கு அவற்றின் குறிப்பிட்ட மூன்று ஒத்த அளவுகள் சமமானவை எனத் தெரிந்தால் போதுமானது. யூக்ளிடிய தளத்திலமையும் இரு முக்கோணங்களின் சர்வசம நிலைப்பாட்டைத் தீர்மானிக்கப் பயன்படுத்தப்படும் எடுகோள்கள் (Postulate):
இரு முக்கோணங்களின் ஒரு சோடி ஒத்தபக்கங்கள் சமமானவையாகவும், அப்பக்கங்களுக்கு இடப்பட்ட கோணங்களும் சமமானவையாகவும் இருந்தால் அவ்விரு முக்கோணங்களும் சர்வசம முக்கோணங்களாக இருக்கும்.
இரு முக்கோணங்களின் மூன்று சோடி ஒத்தபக்கங்களும் சமமானவையாக இருந்தால் அவை முக்கோணங்களாக இருக்கும்.
இரு முக்கோணங்களின் இருசோடி ஒத்த கோணங்கள் சமமாகவும் அக்கோணங்களுக்கு இடைப்பட்ட பக்கங்கள் சம அளவானவையாகவும் இருந்தால் அவ்விரு முக்கோணங்களும் சர்வசமமானவையாகும்.
கிரேக்கக் கணிதவியலாளரான தேலாசால் இந்த எடுகோள் காணப்பட்டது. பெரும்பாலான அடிக்கோள் முறைமைகளில் —பகோப, பபப, கோபகோ— ஆகிய மூன்றும் தேற்றங்களாகக் கருதப்படுகின்றன.
இரு முக்கோணங்களின் இரண்டுகோடி கோணங்கள் சமமானவையாகவும், அக்கோணங்களின் கரங்களாக அமையாத ஒரு சோடி ஒத்தபக்கங்கள் சமமாகவும் இருந்தால் அவ்விரு முக்கோணங்களும் சர்வசமமானவை.
இரு செங்கோண முக்கோணங்களின் செம்பக்கங்கள் சமமானவையாகவும்,, செங்கோணத்தின் கரங்களாக அமையும் பக்கங்களில் எவையேனும் ஒரு ஒத்த சோடிபக்கங்கள் சமமானவையாகவும் இருந்தால் அவ்விரு முக்கோணங்களும் சர்வசமமானவை.
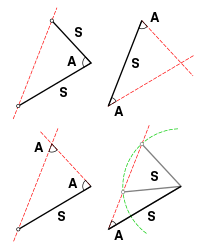
இரு முக்கோணங்கள் சர்வசமமானவையா என்பதைத் தீர்மானிப்பதற்கு பபகோ (பக்கம்-பக்கம்-கோணம்) கட்டுபாடு போதுமானது இல்லை. அதாவது இரு சோடி பக்கங்கள் சமமானவையாகவும், அவற்றால்இடைப்படாத ஒருசோடிக் கோணங்கள் சமமானவையாகவும் இருந்தால், அதனைக் கொண்டு அவ்விரு முக்கோணங்கள் சர்வசமமானவையா என்பதைக் கூற முடியாது. சர்வசமமானயா என்பதைத் தீர்மானிப்பதற்கு இக்கூற்றுடன் கூடுதலான விவரங்களும் தேவைப்படும்:
இரு முக்கோணங்களின் மூன்று சோடிக் கோண அளவுகளும் சமமானவையாக இருந்தால் அவை சர்வசமமான முக்கோணங்களாக இருக்காது. பக்க அளவுகளைப் பற்றி எதுவும் அறியப்படாத நிலையில், அவை வடிவொத்த முக்கோணங்களாக மட்டுமே இருக்கும்.
கோள வடிவவியல், அதிபரவளைய வடிவவியல் இரண்டிலும் ஒரு முக்கோணத்தின் மூன்று கோண அளவுகளின் கூடுதல் அம்முக்கோணத்தின் அளவைப் பொறுத்தது மாறும் என்பதால் ஒரு வளை பரப்பின்மீதமைந்துள்ள இருமுக்கோணங்கள் சர்வசமமானவையா என்பதைத் தீர்மானிக்க கோணம்-கோணம்-கோணம் கட்டுபாடு போதுமானதாகும்.[3]
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.