கணிதத்தில் சமச்சீர்மை

கணிதத்தில் சமச்சீர்மை அல்லது சமச்சீர் (Symmetry) ஆனது, வடிவவியலில் மட்டுமல்லாது ஏனைய பிரிவுகளிலும் காணப்படுகிறது. ஒரு பொருளானது குறிப்பிட்ட சில உருமாற்றங்களின்கீழ் அதன் சில அளவீடுகள் மாற்றமுறாமல் அமையும் பண்பே சமச்சீர்மையாகும். ஒரு கட்டமைப்புள்ள பொருள் X ஐ அதன் கட்டமைப்பு மாறாமல் X ஆகவே மாற்றும் கோப்பாக சமச்சீர் அமைகிறது. எடுத்துக்காட்டாக,

• X என்பது வேறெந்த கூடுதலமைப்பும் கொண்டிராத கணமெனில், சமச்சீரானது அக்கணத்தை அதே கணத்திற்கு இணைக்கும் இருவழிக்கோப்பாகும். இதன் விளைவாக வரிசைமாற்றுக் குலங்கள் கிடைக்கின்றன.
• X என்பது மெட்ரிக் வெளியிலமைந்த ஒரு தளத்தின் புள்ளிகளின் கணமெனில் சமச்சீரானது அக்கணத்தை அதே கணத்துடன் இணைக்கும் இருவழிக்கோப்பாக இருக்கும். மேலும் இந்த இருவழிக்கோப்பின் கீழ் X இன் எந்தவிரு புள்ளிகளுக்கு இடைப்பட்ட தூரம் மாறாமல் பாதுகாக்கப்படும். அதாவது இக்கோப்பு ஒரு சமவளவை உருமாற்றமாகும்.

வடிவவியலில் சமச்சீர்

முதன்மைக் கட்டுரை: சமச்சீர் (வடிவவியல்)

மும்மடி சுழற்சி சமச்சீர் கொண்ட டிரைஸ்கேலீயான்.

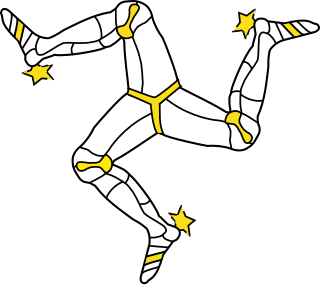
ஒரு வடிவவியல் வடிவை இரண்டு அல்லது இரண்டுக்கும் மேற்பட்ட முற்றொத்த துண்டுகளாகப் பிரிக்க முடியுமானால் அவ்வடிவம் சமச்சீரானதாகக் கொள்ளப்படுகிறது.^[1] அதாவது, முழுவடிவில் மாற்றமின்றி வடிவின் தனித்தனிப் பகுதிகளை நகர்த்தும், ஒரு உருமாற்றம் இருக்குமானால் அவ்வடிவம் சமச்சீர்மை உடையது. இவ்வகையான சமச்சீர்மையானது அவ்வடிவின் தனித்தனித் துண்டுகள் அடுக்கப்பட்ட அமைவு அல்லது உருமாற்றத்தின் வகையைப் பொறுத்தது:

• ஒரு வடிவின் வழியே செல்லும் கோடொன்று ஒன்றுக்கொன்று ஆடி எதிருருக்களாக அமையும் இரு துண்டுகளாக அவ்வடிவைப் பிரிக்குமானால் அவ்வடிவம் எதிரொளிப்பு சமச்சீர்மை கொண்டதாகும்.^[2]
• ஒரு வடிவை அதன் மொத்தவடிவில் எந்தவொரு மாற்றமில்லாமல் ஒரு நிலையான புள்ளியைப் பொறுத்துச் சுழற்ற முடியுமானால் அவ்வடிவம் சுழற்சி சமச்சீர்மை கொண்டதாகும்.^[3]
• ஒரு வடிவை அதன் மொத்த வடிவில் எந்தவொரு மாற்றமில்லாமல் பெயர்ச்சியடையச் செய்ய முடியுமானால் அவ்வடிவம் பெயர்ச்சி சமச்சீர்மை கொண்டதாகும்.^[4]
• முப்பரிமாண வெளியிலமைந்த ஒரு பொருளை ஒரு கோட்டில் (”திருகு அச்சு”) ஒரே சமயத்தில் பெயர்க்கவும், சுழற்றவும் முடியுமானால் அப்பொருள் திருகுசுருள் சமச்சீர்மை கொண்டதாகும்.^[5]
• பெருக்கம் அல்லது குறுக்கத்தால், ஒரு பொருளின் வடிவில் மாற்றமுறவில்லை எனில் அப்பொருள் அளவுமாற்றச் சமச்சீர்மை கொண்டதாகும்.^[6] பகுவலும் ஒருவகையான அளவேற்ற சமச்சீர்மையுடையதாகும். பகுவலின் சிறு பகுதிகள் அதன் பெரிய பகுதிகளோடு வடிவொத்தவையாக இருக்கும்.^[7]
• சறுக்கு எதிரொளிப்பும், சுழல் எதிரொளிப்பும் சமச்சீர்களாகும்.

நுண்கணிதத்தில் சமச்சீர்மை

இரட்டைச் சார்புகள்

முதன்மைக் கட்டுரை: இரட்டைச் சார்பு

ƒ(x) = x², இரட்டைச் சார்புக்கு ஒரு எடுத்துக்காட்டு.

f(x) , மெய்யெண் மாறியில் வரையறுக்கப்பட்ட ஒரு மெய்மதிப்புச் சார்பு, இரட்டைச் சார்பு எனில் பின்வருமாறு வரையறுக்கப்படுகிறது:

f இன் ஆட்களத்திலுள்ள அனைத்து x களுக்கும்,

${\displaystyle f(x)=f(-x).\,}$

இரட்டைச் சார்பின் வரைபடம் y-அச்சைப் பொறுத்து சமச்சீரானது.

எடுத்துக்காட்டுகள்:

• தனிமதிப்புச் சார்பு: ${\displaystyle f(x)=|x|}$
• ${\displaystyle f(x)=x^{2}}$,
• ${\displaystyle f(x)=x^{4}}$
• முக்கோணவியல் சார்பு: ${\displaystyle f(x)=cosx,}$
• அதிபரவளையச் சார்பு: ${\displaystyle f(x)=coshx,}$

ஒற்றைச் சார்புகள்

முதன்மைக் கட்டுரை: ஒற்றைச் சார்பு

ƒ(x) = x³, ஒற்றைச் சார்புக்கு ஒரு எடுத்துக்காட்டு.

மெய்யெண் மாறியில் வரையறுக்கப்பட்ட ஒரு மெய்மதிப்புச் சார்பு f(x), ஒற்றைச் சார்பு எனில் பின்வருமாறு வரையறுக்கப்படுகிறது:

f இன் ஆட்களத்திலுள்ள அனைத்து x களுக்கும்,

${\displaystyle -f(x)=f(-x),\,}$

அல்லது

${\displaystyle f(x)+f(-x)=0.\,}$

ஒற்றைச் சார்புகளின் வரைபடம் ஆதிப்புள்ளியைப் பொறுத்து சமச்சீர் சுழற்சி கொண்டிருக்கும். அதாவது ஆதிப்புள்ளியைப் பொறுத்து 180 பாகைகள் சுழற்றப்படும்போது ஒற்றைச் சார்புகளின் வரைபடத்தில் எந்தவித மாற்றமும் இருக்காது.

எடுத்துக்காட்டுகள்:

• ${\displaystyle f(x)=x\,}$
• ${\displaystyle f(x)=x^{3}\,}$
• ${\displaystyle f(x)=sinx\,}$
• ${\displaystyle f(x)=sinhx\,}$
• பிழைச் சார்பு ${\displaystyle \operatorname {erf} (x)}$

தொகையிடல்

ஒரு ஒற்றைச் சார்பின் −A முதல் +A வரையிலான வரையறுத்த தொகையின் மதிப்பு பூச்சியமாகும். (A முடிவுறு மதிப்பு மற்றும் −A , A இவற்றுக்கிடையே இச்சார்புக்கு குத்து அணுகுகோடுகளே இல்லாமல் இருக்கவேண்டும்).

ஒரு இரட்டைச் சார்பின் −A முதல் +A வரையிலான வரையறுத்த தொகையின் மதிப்பு அச்சார்பின் 0 முதல் +A வரையிலான வரையறுத்த தொகையின் மதிப்பைப் போல இருமடங்காகும். (A முடிவுறு மதிப்பு மற்றும் −A , A இவற்றுக்கிடையே இச்சார்புக்கு குத்து அணுகுகோடுகளே இல்லாது இருக்க வேண்டும். தொகையீடு ஒருங்கும்போது மட்டும், A முடிவிலி மதிப்பு என்றாலும் இம்முடிவு உண்மையாக இருக்கும்).

தொடர்கள்

• ஒரு இரட்டைச் சார்பின் டெய்லர் தொடர் இரட்டை அடுக்கு உறுப்புகளையே கொண்டிருக்கும்.
• ஒற்றைச் சார்பின் மெக்லாரின் தொடர் ஒற்றை அடுக்கு உறுப்புகளையே கொண்டிருக்கும்..
• ஒரு காலமுறை இரட்டைச் சார்பின் ஃபூரியே தொடர் கொசைன்உறுப்புகளை மட்டுமே கொண்டிருக்கும்.
• ஒரு காலமுறை ஒற்றைச் சார்பின் ஃபூரியே தொடர் சைன்உறுப்புகளை மட்டுமே கொண்டிருக்கும்.

நேரியல் இயற்கணிதத்தில் சமச்சீர்மை

அணிகளில் சமச்சீர்மை

நேரியல் இயற்கணிதத்தில், ஒரு சதுர அணியானது அதன் இடமாற்று அணிக்குச் சமமாக இருந்தால் அது சமச்சீர் அணி எனப்படும்.

சதுர அணி A ஒரு சமச்சீர் அணி எனில்:

${\displaystyle A=A^{\top }}$

இரு அணிகள் சமமாக இருக்கவேண்டுமானால் அவற்றின் வரிசைகள் (நிரைXநிரல்) சமமாக இருக்க வேண்டும் என்பதால் சதுர அணிகள் மட்டுமே சமச்சீர் அணிகளாக இருக்க முடியும்.

ஒரு சமச்சீர் அணியின் உறுப்புகள் அதன் முதன்மை மூலைவிட்டத்தைப் பொறுத்து சமச்சீராக இருக்கும். எனவே,

A = (a_ij) அனியில்:

a_ij = a_ji (அனைத்து சுட்டுகள் i மற்றும் j மதிப்புகளுக்கும்)

கீழுள்ள 3×3 அணி சமச்சீரானது:

${\displaystyle {\begin{bmatrix}1&7&3\\7&4&-5\\3&-5&6\end{bmatrix}}.}$

ஒரு மூலைவிட்ட அணியில் முதன்மை மூலைவிட்ட உறுப்புகள் தவிர்த்த பிற உறுப்புகள் பூச்சியமாக இருக்கும் என்பதால், ஒவ்வொரு மூலைவிட்ட அணியும் சமச்சீர் அணியாக இருக்கும். அதுபோலவே எதிர் சமச்சீர் அணியின் மூலைவிட்ட உறுப்புகள் தனக்குத்தாமே எதிரெண்ணாக இருக்க வேண்டுமென்பதால் அவை அனைத்தும் பூச்சியமாகும்.

நுண் இயற்கணிதத்தில் சமச்சீர்மை

சமச்சீர் குலங்கள்

முதன்மைக் கட்டுரை: சமச்சீர் குலம்

n குறிகள் கொண்ட முடிவுறு கணத்தின் சமச்சீர் குலம் S_n என்பது அக்குறிகளின் வரிசைமாற்றங்களின் தொகுப்புச் செயலியுடன், அக்குறிகளின் வரிசைமாற்றங்களாலான குலமாகும். இவ்வரிசைமாற்றங்கள், குறிகளின் கணத்திலிருந்து அதே கணத்திற்கு வரையறுக்கப்படும் இருவழிக்கோப்பாகக் கருதப்படும்.^[8] n உறுப்புகளின் வரிசைமாற்றங்களின் எண்ணிக்கை n! (n தொடர் பெருக்கம்) என்பதால் இச்சமச்சீர் குலம் S_n இன் வரிசை (உறுப்புகளின் எண்ணிக்கை) n! ஆகும்.

சமச்சீர் பல்லுறுப்புக்கோவைகள்

முதன்மைக் கட்டுரை: சமச்சீர் பல்லுறுப்புக்கோவை

P(X₁, X₂, …, X_n) என்பது n மாறிகளில் அமைந்த ஒரு பல்லுறுப்புக்கோவை. இப்பல்லுறுப்புக்கோவையின் மாறிகளில் ஒன்றை மற்றொன்றால் பதிலிட்டாலும் பல்லுறுப்புக்கோவையில் மாற்றமில்லையெனில் அது சமச்சீர் பல்லுறுப்புக்கோவை எனப்படும்.

P(X₁, X₂, …, X_n) ஒரு சமச்சீர் பல்லுறுப்புக்கோவை மற்றும் σ என்பது மாறிகளின் கீழொட்டுகளின் (1, 2, ..., n) ஏதாவதொரு வரிசைமாற்றம் எனில்:

P(X_σ(1), X_σ(2), …, X_σ(n)) = P(X₁, X₂, …, X_n).

எடுத்துக்காட்டுகள்

• இருமாறிகளிலமைந்த சமச்சீர் பல்லுறுப்புக்கோவை (X₁, X₂):

${\displaystyle X_{1}^{3}+X_{2}^{3}-7}$

${\displaystyle 4X_{1}^{2}X_{2}^{2}+X_{1}^{3}X_{2}+X_{1}X_{2}^{3}+(X_{1}+X_{2})^{4}}$

• மூன்று மாறிகளிலமைந்த சமச்ச்சீர் பல்லுறுப்புக்கோவை (X₁, X₂, X₃):

${\displaystyle X_{1}X_{2}X_{3}-2X_{1}X_{2}-2X_{1}X_{3}-2X_{2}X_{3}\,}$

இயற்கணிதப் பொருட்களின் தன்னமைவியங்கள்

நுண் இயற்கணிதத்தில், தன்னமைவியம் (automorphism) என்பது ஒரு கணிதப் பொருளிலிருந்து அதே பொருளுக்கு அமையும் ஒரு சமவமைவியமாகும். ஒருவகையில் இது அப்பொருளின் சமச்சீர்மையாக அல்லது அப்பொருளின் அனைத்து அமைப்புகளையும் பாதுகாக்கும் கோப்பாக அமையும். ஒரு கணிதப் பொருளின் தன்னமைவியங்கள் அனைத்தும் ஒரு குலமாகும். இக்குலம் ”தன்னமைவியக் குலம்” என அழைக்கப்படும்.

எடுத்துக்காட்டுகள்

• கணக் கோட்பாட்டில், X கணத்தின் உறுப்புகளின் ஏதேனுமொரு வரிசைமாற்றம் ஒரு தன்னமைவியமாகும். X கணத்தின் தன்னமைவியக் குலமானது X இன் மீதான சமச்சீர் குலம் எனவும் அழைக்கப்படும்.
• அடிப்படை எண்கணிதத்தில் முழு எண்களின் கணம் Z கூட்டலின் கீழ் ஒரு குலமாகும். மேலும் எதிராக்கம் (negation) இக்கணத்தின் தனித்ததொரு தன்னமைவியம். முழுஎண்களின் கணத்தை வளையமாகக் கொண்டால் அதற்கு அற்ப தன்னமைவியம் மட்டுமே உண்டு. எனவே பொதுவாக, எந்தவொரு பரிமாற்றுக் குலத்திற்கும் தன்னமைவியமாக இருக்கும்; ஆனால் வளையத்திற்கோ அல்லது களத்திற்கோ தன்னமைவியமாக இருக்காது.

குலக் கோட்பாட்டில் சமச்சீர்மை

சமச்சீர் உறவு

முதன்மைக் கட்டுரை: சமச்சீர் உறவு

கணிதத்தில், ஒரு கணத்தில் வரையறுக்கப்பட்ட ஈருறுப்பு உறவு சமச்சீர் உறவு (symmetric) எனில், அவ்வுறவின்கீழ் அக்கணத்தில் உள்ள ஒவ்வொரு சோடி உறுப்புகளுக்கும், சோடியின் முதல் உறுப்புக்கு இரண்டாவது உறுப்புடன் உறவு உண்டெனில், இரண்டாவது உறுப்புக்கும் முதல் உறுப்புடன் உறவு இருக்கும்.

X கணத்தில் வரையறுக்கப்பட்ட ஈருறுப்பு உறவு R ஒரு சமச்சீர் உறவு எனில்:

${\displaystyle \forall a,b\in X,\ aRb\Rightarrow \;bRa.}$

சமச்சீர் உறவானது எதிர்சமச்சீர் உறவுக்கு நேர் எதிரானதல்ல என்பதும் குறிப்பிடத்தக்கது.

வகையீட்டுச் சமன்பாடுகளின் சமச்சீர்

ஒரு வகையீட்டுச் சமன்பாட்டை எந்தவொரு மாற்றமுமின்றி விட்டுவைக்கும் உருமாற்றம் அச்சமன்பாட்டின் சமச்சீர் ஆகும். வகையீட்டுச் சமன்பாடுகளைத் தீர்ப்பதற்கு இச்சமச்சீர்கள் உதவியாய் இருக்கும்.

ஒரு வகையீட்டுச் சமன்பாட்டுத் தொகுதியின் எதிரொளிப்பு சமச்சீர்மை என்பது அத்தொகுதியின் தொடர் சமச்சீராகும். ஒரு சாதாரண வகையீட்டுச் சமன்பாட்டின் வரிசைக் குறைப்பின் மூலம் அச்சமன்பாட்டை எளிதானதாக்க கோட்டு சமச்சீர் உதவும்.^[9]

நிகழ்தகவில் சமச்சீர்

முடிவுறு எண்ணிக்கையில் நிகழக்கூடிய விளைவுகளைக் கொண்ட நிகழ்ச்சியில் வரிசைமாற்றங்களைப் பொறுத்த சமச்சீரால் ஒரு சீரான தனித்த பரவல் அமையும்.

மெய்யெண் இடைவெளியில் அமையும் விளைவுகளைக் கொண்ட நிகழ்ச்சியில் சமநீள உள் இடைவெளிகளை ஒன்றுக்கொன்று பரிமாற்றுவது பொறுத்த சமச்சீரல் ஒரு சீரான தொடர் பரவல் அமையும்.

"சமவாய்ப்பு முறையில் ஒரு முழுஎண்ணைத் தேர்ந்தெடுத்தல்" அல்லது "சமவாய்ப்பு முறையில் ஒரு மெய்யெண்ணைத் தேர்ந்தெடுத்தல்" போன்ற பிற நிகழ்ச்சிகளில், வரிசைமாற்றங்கள் அல்லது சமநீள உள்ளிடைவெளி பரிமாற்றம் பொறுத்த சமச்சீருடைய நிகழ்தகவுப் பரவல்களே கிடையாது. வேறெந்த நியாயமான சமச்சீர்களும் ஒரு குறிப்பிட்ட நிகழ்தகவுப் பரவலைத் தருவதில்லை. அதாவது, அதிகபட்ச சமச்சீரைத் தரும் தனித்ததொரு நிகழ்தவுப் பரவல் எதுவும் இல்லை.

ஒரு புள்ளியில் எதிரொளிப்பு -இந்த ஒரு பரிமாண சமவமைவியமானது, நிகழ்தகவுப் பரவலை மாற்றாமல் வைத்திருக்கும்.

விளைவுகளும் அவற்றின் தலைகீழிகளும் ஒரே பரவலைக் கொண்டிருக்குமானல், நேர்ம விளைவுகளைக் கொண்ட சமவாய்ப்புச் சோதனைகளுக்கு சமச்சீர் இருக்கக்கூடிய வாய்ப்புண்டு. எனினும் இச்சமச்சீர் ஒரு தனித்ததொரு பரவலைக் குறிப்பதில்லை.

ஒரு ஆதிப்புள்ளியைத் தேர்ந்தெடுப்பதன் மூலம் தளம் அல்லது வெளியிலமைந்த ஒரு "சமவாய்ப்புப் புள்ளி"க்கு முறையே வட்ட அல்லது கோளச் சமச்சீர் கொண்ட ஒரு நிகழ்தகவுப் பரவலைக் காண முடியும்.

மேற்கோள்கள்

1. E. H. Lockwood, R. H. Macmillan, Geometric Symmetry, London: Cambridge Press, 1978
2. Weyl, Hermann (1982) [1952]. Symmetry. Princeton: Princeton University Press. பன்னாட்டுத் தரப்புத்தக எண் 0-691-02374-3.
3. Singer, David A. (1998). Geometry: Plane and Fancy. Springer Science & Business Media.
4. Stenger, Victor J. (2000) and Mahou Shiro (2007). Timeless Reality. Prometheus Books. Especially chapter 12. Nontechnical.
5. Bottema, O, and B. Roth, Theoretical Kinematics, Dover Publications (September 1990)
6. Tian Yu Cao Conceptual Foundations of Quantum Field Theory Cambridge University Press p.154-155
7. Gouyet, Jean-François (1996). Physics and fractal structures. Paris/New York: Masson Springer. பன்னாட்டுத் தரப்புத்தக எண் 978-0-387-94153-0.
8. Jacobson (2009), p. 31.
9. Olver, Peter J. (1986). Applications of Lie Groups to Differential Equations. New York: Springer Verlag. பன்னாட்டுத் தரப்புத்தக எண் 978-0-387-95000-6.

ஆதார நூல்கள்

• Hermann Weyl, Symmetry. Reprint of the 1952 original. Princeton Science Library. Princeton University Press, Princeton, NJ, 1989. viii+168 pp. பன்னாட்டுத் தரப்புத்தக எண் 0-691-02374-3
• Mark Ronan, Symmetry and the Monster, Oxford University Press, 2006. பன்னாட்டுத் தரப்புத்தக எண் 978-0-19-280723-6 (Concise introduction for lay reader)
• Marcus du Sautoy, Finding Moonshine: a Mathematician's Journey through Symmetry, Fourth Estate, 2009