Карл Фридрих Гаус

Јохан Карл Фридрих Гаус ( ; Брауншвајг, 30. април 1777 — Гетинген, 23. фебруар 1855) био је немачки математичар и научник који је дао значајан допринос у многим пољима, укључујући теорију бројева, анализу, диференцијалну геометрију, геодезију, електростатику, астрономију и оптику.^[1][2] Познат као „принц математичара“^[3] и „највећи математичар од давнина“, Гаус је оставио траг на многим пољима математике и науке и сматра се једним од најутицајнијих математичара у историји.^[4]

Карл Фридрих Гаус
Гаусов портрет, слика Кристијана Јенсена
Датум рођења	(1777-04-30)30. април 1777.
Место рођења	Брауншвајг, Немачка
Датум смрти	23. фебруар 1855.(1855-02-23) (77 год.)
Место смрти	Гетинген, Хановер, Немачка
Образовање	Универзитет у Хелмштету, Универзитет у Гетингену
Поље	математика, физика
Институција	Универзитет Георг-Аугуст, Гетинген
Ученици	Ричард Дедекинд Бернард Риман
Познат по	Теорија бројева, магнетизам
Награде	Коплијева медаља (1838)
Потпис

(1801)

Црвена крива преставља стандардизирану нормалну расподелу.

Изванредну математичку даровитост показао већ у детињству, а прве научне резултате постигао као студент математике у Гетингену. У вези с теоријом дељења круга решио је (1796) проблем конструкције правилних полигона лењиром и шестаром, доказавши да се за неки прости број може на тај начин конструисати правилни -троугао онда и само онда када је Фермаов број, то јест број облика , а као такви су данас познати само 3, 5, 17, 257 и 65 537. Промовисан је 1799. године на темељу докторске дисертације, у којој је доказао изванредно значајан фундаментални теорем алгебре. Делом истраживања у аритметици (лат. , 1801) поставио је основе савременој теорији бројева. Његова Општа истраживања закривљених површина (лат. , 1828) нова су етапа у развоју диференцијалне геометрије и основица њеног напретка све до данас. У томе делу он уводи систематску употребу параметарског представљања површина, две основне квадратне форме, сферно пресликавање и на основи тога појам закривљености у тачки површине. Доказана је и основна теорема о инваријантности закривљености површине при њеном изометричком пресликавању (лат. ). Значајан је и његов прилог теорији грешака при мерењу, изложен као теорија најмањих квадрата у делу Теорија комбиновања уз најмање грешке опажања (лат. 1821—1826), према којој је најпогоднија вредност мерене величине она за коју је збир квадрата грешака најмањи.

Открића настала приликом проучавања Земљинога магнетскога поља изложио је у делу Општа теорија магнетизма Земље ( , 1839). Примењивао је математику на описивање електричних и магнетних појава (на пример Гаусов закон за магнетно поље и Гаусов закон за електрично поље). Бавио се оптиком (Гаусова апроксимација).^[5] Посебно су значајна његова истраживања у подручју основа геометрије, премда о томе није ништа објавио. Још и пре Н. И. Лобачевскога и Јаноша Бољаја спознао је логичку могућност геометрије различите од еуклидске геометрије и открио у њој низ основних чињеница. Посмртно објављена његова научна оставштина подстакнула је занимање за нееуклидске геометрије и допринела је њиховом бржем развоју. По њему су названи кратер на Месецу (Гаусов кратер) и планетоид (1001 Гаусија).^[6]

Биографија

Статуа Гауса у његовом родном месту, Брауншвајгу

Јохан Карл Фридрих Гаус је рођен 30. априла 1777. године у Брауншвајгу, у грофовији Брауншвајг-Волфенбитела (сада делу Доње Саксоније, Немачка), као син сиромашних родитеља из радничке класе.^[7] Његова мајка је била неписмена. Датум његовог рођења није записан, мада је било познато да се родио у среду, осам дана пре Васкрса. Гаус је касније решио загонетку свог датума рођења у контексту налажења датума Васкрса, изводећи методе за израчунавање датума у прошлим и будућим годинама.^[8] Он је био крштен у цркви у близини школе коју је похађао као дете.^[9]

Већ су у основној школи били изненађени његовим брзим сабирањем бројева од 1 до 100, када је закључио да збир 50 парова бројева (први и последњи, други и претпоследњи, итд.) износи 101: 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101 итд. Проучавао је античке језике у гимназији .^[10][11] У његовој 17 години гроф од Брауншвајг-Волфенбитела му даје стипендију,^[4] те се уласком у колегијум Каролинум заинтересовао за математику и самостално открио^[12] Бодеов закон пропорција, допринео теорији квадратних форми, аритметичкој средини, геометријској средини, закону квадратне реципрочности,^[13] те теореми о простим бројевима. С тим открићима одустао је од проучавања језика и окренуо се математици.

Математика

Студирао је на Гетингенском универзитету од 1795. до 1798, где му је учитељ био Кестнер којег је често исмејавао; а докторирао је 1799, доказавши да свака алгебарска једначина има најмање једно решење. Та теорема се назива основном теоремом алгебре. Ту је покушао да конструише правилни седмоугао помоћу лењира и шестара. Не само да је дошао до закључка да је то немогуће, већ је открио методе конструкције правилног 17, 257, 65537 – угла. Тако је доказао да је конструкција правилног многоугла, лењиром и шестаром, могућа само када су странице прим бројеви серије 3, 5, 17, 257, 65537 и тако даље; то је описао у књизи о теорији бројева, (Питања о аритметици, 1801), које је класично дело на пољу математике.

Гаусова расподела

Главни чланак: Нормална расподела

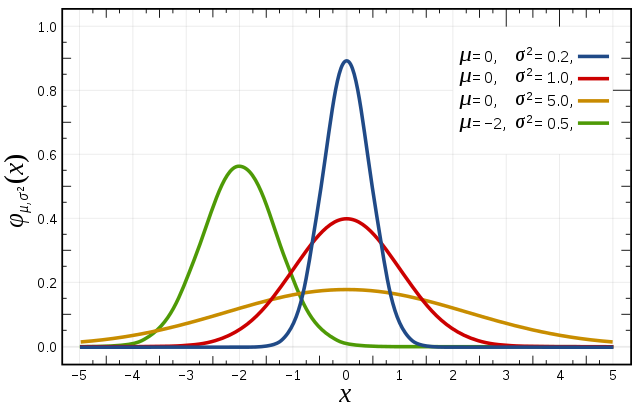
Нормална расподела, Гаусова расподела или Гаус-Лапласова расподела је најважнија статистичка теоријска расподела (дистрибуција). Први ју је објаснио Абрам де Моавр (1753) као гранични облик биномне расподеле. Нормална расподела је апсолутно непрекидна расподела чија густина је облика:

${\displaystyle f(x\;|\;\mu ,\sigma )={\frac {1}{\sigma {\sqrt {2\pi }}}}\;e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}}$

Она је двопараметарска функција. Параметри су јој математичко очекивање μ и стандардна девијација σ. Стандардизована нормална расподела има математичко очекивање ${\displaystyle \mu =0}$ и стандардну девијацију ${\displaystyle \sigma =1}$, а бележи се као ${\displaystyle N(0,1)}$. Нормална крива (то јест граф нормалне расподеле) звоноликог је облика и симетрична је, па су сви непарни моменти око математичког очекивања расподеле једнаки 0. Математичко очекивање, медијана и модус нормалне расподеле међусобно су једнаки, што је последица својства симетричности густине ове расподеле. Коефицијенти асиметрије једнаки су 0, а коефицијент заобљености је 3.^[14]

Гаусова крива

Главни чланак: Гаусова крива

Гаусова крива је крива одређена једначином:

${\displaystyle y=e^{-x^{2}}}$

симетрична је с обзиром на y-осу, асимптотски се приближује ка x-оси, када x тежи према . Та се крива, због њене примене у рачуну вероватноће, назива и кривом вероватноће.^[15]

Гаусов алгоритам

Главни чланак: Гаусов алгоритам

Гаусов алгоритам је низ математичких операција, које је предложио Гаус за решавање система линеарних једначина. Начин на који се поништавају (елиминишу) поједине непознате у једначинама познат је и под именом Гаусове елиминације.^[16]

Астрономија

Гаус се након тога посветио астрономији те је по његовим прорачунима планетоид Церес, откривен 1801. Дао је такође нову методу израчунавања путања или орбита небеских тела. Године 1807, након смрти Грофа од Брунсвика, постао је математички професор и директор опсерваторије у Гетингену, где је остао све до своје смрти 1855. Након низа породичних трагедија, 1809. издаје своју другу књигу у два дела , о кретању небеских тела. У првом делу расправља о диференцијалним једначинама, деловима купе и елиптичним орбитама, док у другом, главном делу показује како се може наћи и израчунати орбита планета. Гаусов допринос теоријској астрономији престаје након 1817, иако наставља с посматрањима. Иако у опсерваторији проводи већину времена, налази времена и за рад на другим подручјима науке. Његова дела из тог периода су: , увод у теорију хипергеометријских функција; , практични есеј о интегралном рачуну, , расправа о статистичким проценама, те , инспирисана геометријским проблемима.

Геодезија

Гаус се током 1820-их све више интересовао за геодезију. Године 1818. спроводио је геодетска истраживања за државу Хановер, о спајању с данском жељезничком мрежом, те је изумео хелиотроп (справу за сигнализацију на даљину), који је радио на начелу рефлектовања сунчевих зрака помоћу телескопа и огледала. Од 1820. до 1830. издао је више од 70 чланака. Године 1822. освојио је награду Копенхагенског универзитета с делом . Гаус је први развио нееуклидску геометрију, дискутујући са Фаркашом Болјајом, Јаношом Болјајом и Лобачевским.^[17][18][19] Проучавао је диференцијалну геометрију, те је о тој теми написао дело (1828), његово најважније дело на том подручју, које садржи идеје као Гаусова крива (нормалан граф вероватноће) и теорем егрегриум. По Гаусу је назван и Гаус-Кригеров координатни систем који је усвојен као званична државна картографска пројекција у Краљевини СХС 1924. године^[20] и коришћен у Републици Србији до 2011. године^[21].

Физика

Са немачким физичаром Вилхелм Едуард Вебером, Гаус је спровео опширно истраживање о магнетизму, а његово примењивање математике на магнетизам и електрицитет је једно од његових важнијих доприноса (у част њему јединица интензитета магнетског поља добила је назив гаус). О тој је теми написао многа дела као: (1832), (1839) и (1840).^[22] Гаус и Вебер су открили Кирхофове законе, конструисали примитивни телеграф те створили властите новине . Међу његовим задњим делима је расправа с Герлингом о Фукоовом клатну (1854).^[23][24] Доживео је отворење хановерске железничке мреже, те је преминуо 23. фебруара 1855. у Гетингену, а да ретко које поље математике, астрономије и математичке физике није остало дотакнуто његовим доприносима. Његов мозак је сачуван и изучавао га је Rudolf Ваgner, који је утврдио да је његова маса 1.492 грама (нешто изнад просека) и да је церебрална област једнака 219.588 квадратна милиметра^[25] Високо развијене конволуције су исто тако уочене, што је у раном 20. веку сматрано објашњењем његовог генија.^[26]

Гаусов закон електричнога поља

Главни чланак: Гаусов закон

Гаусов закон електричнога поља је физички закон према којем су линије електричнога поља отворене криве што излазе из позитивних електричних набоја, а завршавају у негативним електричним набојима, односно ток електричнога поља кроз замишљену затворену површину једнак је збиру свих електричних набоја који се налазе унутар те површине подељене с диелектричном пермитивношћу вакуума. У интегралном облику закон гласи:

${\displaystyle \Phi _{E}={\frac {Q}{\varepsilon _{0}}}}$

где је: Φ_E - ток електричног поља, Q - електрични набој, ε₀ - диелектрична константа вакуума. Ток се надаље може повезати са електричним пољем:

${\displaystyle \Phi _{E}=\int _{s}E\cdot dA}$

где је: - вектор електричног поља, а - елемент површине по којој се интегрише. Ток електричнога поља кроз произвољну затворену површину која не садржи електрични набој једнак је нули, то јест електрични набој извор је електричног поља.^[27]

Гаусов закон магнетскога поља

Главни чланак: Гаусов закон магнетскога поља

Гаусов закон магнетскога поља је физички закон према којему су линије магнетскога поља затворене линије, односно магнетски ток (ток вектора магнетске индукције) кроз замишљену затворену површину једнак је нули:

${\displaystyle \iint \mathbf {B} \cdot dS=0}$

где је: - магнетски ток, а - затворена површина. Тим је законом потврђено да у природи не постоје магнетски монополи.^[28]

Гаусов систем јединица

Главни чланак: ЦГС сисем

Гаусов систем јединица је систем мерних јединица који је на темељу предлога Гауса и В. Вебера прихваћен на 1. међународном електротехничком конгресу у Паризу 1881. и сматран јединственим системом јединица свеукупне науке. Основне су му јединице биле центиметар, грам и секунда, по чему је назван ЦГС-системом. Због кривих тумачења замисли његових оснивача, у примени је тога система било много тешкоћа, посебно у подручју електромагнетизма. Електричне су се величине изражавале јединицама ЦГСе-система (електростатички систем јединица), а магнетске јединицама ЦГСм-система (електромагнетски систем јединица). За такав мешовити, некохерентни систем предложио је Херман фон Хелмхолц 1882. назив Гаусов систем јединица. Уз друге системе примењивао се седамдесетак година, посебно у физици. Сва су 3 система данас замењена Међународним системом мерних јединица (SI).^[29]

Референце

1. Bass et al. 2009, стр. 17.7 harvnb грешка: no target: CITEREFBassDeCusatisEnochVasudevan2009 (help)
2. Ostdiek & Bord 2007, стр. 381
3. Zeidler 2004, стр. 1188.
4. Dunnington, G. Waldo. (May 1927).„The Sesquicentennial of the Birth of Gauss”. Архивирано из оригинала 26. 2. 2008. г. Приступљено 23. 6. 2005. Scientific Monthly XXIV: 402–414. Приступљено 29 June 2005. Now available at = The_Sesquicentennial_of_the_Birth_of_Gauss „The Sesquicentennial of the Birth of Gauss” Проверите вредност параметра |url= (помоћ). Retrieved 23 February 2014. Comprehensive biographical article.
5. Hecht 1987, стр. 134 harvnb грешка: no target: CITEREFHecht1987 (help)
6. Gauss, Carl Friedrich, "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2015.
7. „Carl Friedrich Gauss”. Wichita State University. Архивирано из оригинала 19. 02. 2016. г. Приступљено 30. 07. 2017.
8. „Gauss Birthday Problem”.
9. Chamberless, Susan (11. 3. 2000). = Letter:WORTHINGTON,_Helen_to_Carl_F._Gauss_-_1911-07-26 „Letter:WORTHINGTON, Helen to Carl F. Gauss – 26 July 1911” Проверите вредност параметра |url= (помоћ). Susan D. Chambless. Приступљено 14. 9. 2011.
10. "Gauss, Carl Friedrich (1777–1855)." (2014). In The Hutchinson Dictionary of scientific biography. Abington, United Kingdom: Helicon.
11. Hayes, Brian (14. 11. 2009). „Gauss's Day of Reckoning”. American Scientist. 94 (3): 200. doi:10.1511/2006.3.200. Приступљено 30. 10. 2012.
12. O'Connor, John J.; Robertson, Edmund F. „Карл Фридрих Гаус”. MacTutor History of Mathematics archive. University of St Andrews.
13. Gauss, DA § 4, arts 107–150
14. Normalna distribucija (također Gaussova, Gauss-Laplaceova distribucija), "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2015.
15. Gaussova krivulja, "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2015.
16. Gaussov algoritam, "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2015.
17. Krantz 2010, стр. 171
18. Halsted, G. B. (1912). „Duncan M. Y. Sommerville”. American Mathematical Monthly. 19 (1): 1—4. JSTOR 2973871. doi:10.2307/2973871.
19. Sondow, J. (2014). „From the Monthly Over 100 Years Ago…”. American Mathematical Monthly. 121 (10): 963. S2CID 207521166. arXiv:1405.4198 . doi:10.4169/amer.math.monthly.121.10.963.
20. [Историјат Војногеографског института по годинама, http://www.vgi.mod.gov.rs/cirilica/onama_cir/godine_cir.html Архивирано на сајту (27. август 2014)]
21. Нови државни референтни систем Републике Србије и подела на листове карата и планова, Архивирано на сајту (30. април 2018)
22. Bühler 1987, стр. 144–145
23. Monastyrsky 1987, стр. 21–22
24. Bühler 1987, стр. 154
25. This reference from 1891 (Donaldson, Henry H. (1891). „Anatomical Observations on the Brain and Several Sense-Organs of the Blind Deaf-Mute, Laura Dewey Bridgman”. The American Journal of Psychology. E. C. Sanford. 4 (2): 248—294. JSTOR 1411270. doi:10.2307/1411270.) says: "Gauss, 1492 grm. 957 grm. 219588. sq. mm."; i.e. the unit is square mm. In the later reference: Dunnington (1927), the unit is erroneously reported as square cm, which gives an unreasonably large area; the 1891 reference is more reliable.
26. Bardi 2008, стр. 189
27. Gaussov zakon električnoga polja, "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2015.
28. Gaussov zakon magnetskoga polja, "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2015.
29. Gaussov sustav jedinica, "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2015.

Литература

• Ostdiek, Vern J.; Bord, Donald J. (2007). Inquiry into Physics. Cengage Learning. ISBN 978-0-495-11943-2.
• Bardi, Jason (2008). The Fifth Postulate: How Unraveling A Two Thousand Year Old Mystery Unraveled the Universe. John Wiley & Sons, Inc. ISBN 978-0-470-46736-7.
• Monastyrsky, Michael (1987). Riemann, Topology, and Physics. Birkhäuser. стр. 21–22. ISBN 978-0-8176-3262-5.
• Krantz, Steven G. (2010). An Episodic History of Mathematics: Mathematical Culture through Problem Solving. MAA. стр. 171. ISBN 978-0-88385-766-3. Приступљено 9. 2. 2013.
• Zeidler, Eberhard (2004). Oxford Users' Guide to Mathematics. Oxford, UK: Oxford University Press. стр. 1188. ISBN 978-0-19-850763-5.
• Bass, Michael; DeCusatis, Casimer; Enoch, Jay; Lakshminarayanan, Vasudevan (2009). Handbook of Optics. McGraw Hill Professional. стр. 17.7. ISBN 978-0-07-149889-0.
• Bühler, Walter Kaufmann (1987). Gauss: A Biographical Study. Springer-Verlag. ISBN 978-0-387-10662-5.
• Dunnington, G. Waldo. (2003). Carl Friedrich Gauss: Titan of Science. The Mathematical Association of America. ISBN 978-0-88385-547-8. OCLC 53933110.
• Gauss, Carl Friedrich (1965). Disquisitiones Arithmeticae. tr. Arthur A. Clarke. Yale University Press. ISBN 978-0-300-09473-2.
• Hall, Tord (1970). Carl Friedrich Gauss: A Biography. Cambridge, MA: MIT Press. ISBN 978-0-262-08040-8. OCLC 185662235.
• Kehlmann, Daniel (2005). Die Vermessung der Welt. Rowohlt. ISBN 978-3-498-03528-0. OCLC 144590801.
• Sartorius von Waltershausen, Wolfgang (1856). Gauss: A Memorial. S. Hirzel.
• Simmons, J. (1996). The Giant Book of Scientists: The 100 Greatest Minds of All Time. Sydney: The Book Company.
• Tent, Margaret (2006). The Prince of Mathematics: Carl Friedrich Gauss. A K Peters. ISBN 978-1-56881-455-1.

Спољашње везе

• O'Connor, John J.; Robertson, Edmund F. „Карл Фридрих Гаус”. MacTutor History of Mathematics archive. University of St Andrews.
• Гаусова биографија
• Комплетна дела
• Karl Friedrich Gauss на сајту Пројекат Гутенберг (језик: енглески)
• Карл Фридрих Гаус на сајту Internet Archive (језик: енглески)
• Gauss and his children
• Карл Фридрих Гаус на сајту MGP (језик: енглески)
• Grimes, James. „5050 And a Gauss Trick”. Numberphile. Brady Haran. Архивирано из оригинала 15. 7. 2017. г. Приступљено 30. 7. 2017.